【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,三相ブリッジダイオード整流器の動作に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
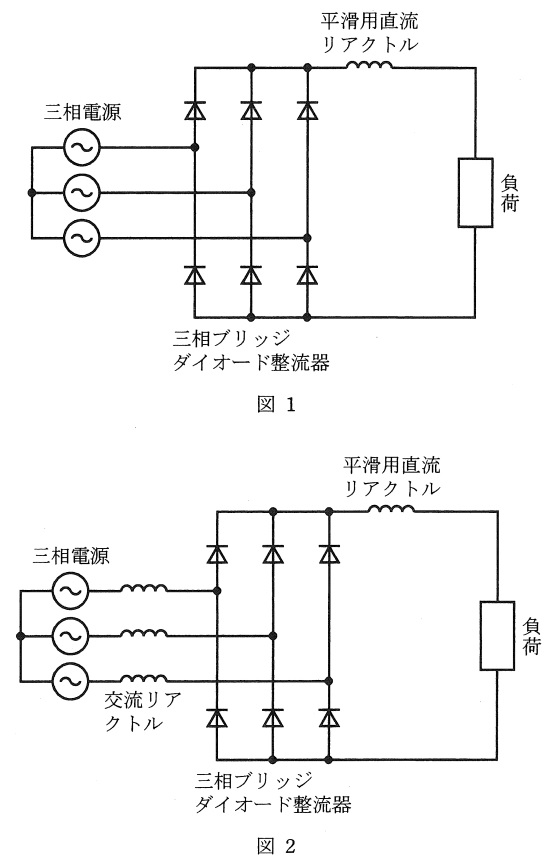
図1は三相ブリッジダイオード整流器の回路構成である。負荷と直列に平滑用直流リアクトルを接続している。ダイオードのオン電圧,逆阻止電流(逆漏れ電流)及び逆回復電流(リカバリ電流),並びにリアクトルの抵抗は無視できるものとする。また,三相電源の内部インピーダンスも無視できるものとする。平滑用直流リアクトルのインダクタンスを増加すると,負荷電流のリプルを低減することができる。平滑用直流リアクトルのインダクタンスが十分に大きいとすると,ダイオード整流器の交流入力電流波形は,通電期間が\( \ \fbox { (1) } \ \)の方形波になる。線間電圧実効値が\( \ 200 \ \mathrm {[V]} \ \),\( \ 50 \ \mathrm {[Hz]} \ \)の三相電源にダイオード整流器を接続した場合,負荷の直流電圧は約\( \ \fbox { (2) } \ \mathrm {[V]} \ \)となる。
一方,図2のように三相電源とダイオード整流器との間に交流リアクトルを接続した場合には,交流リアクトルがない場合と比べて,各ダイオードが\( \ \fbox { (3) } \ \)状態になる時刻に遅れが生じ,\( \ \fbox { (4) } \ \)が発生する。このとき,交流入力電流は台形波状となり,基本波力率は低下するが,高調波ひずみ率は減少する。また,交流リアクトルを接続しない場合と比べて,負荷電圧の電圧変動率は増加する。各相に\( \ 1 \ \mathrm {[mH]} \ \)の交流リアクトルを接続したとき,負荷電流が\( \ 100 \ \mathrm {[A]} \ \)流れたとすると,負荷電圧は約\( \ \fbox { (5) } \ \mathrm {[V]} \ \)低下する。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 20 &(ロ)& 制御遅れ角 &(ハ)& 180 \ [°] \\[ 5pt ]
&(ニ)& 245 &(ホ)& 60 \ [°] &(ヘ)& 保 持 \\[ 5pt ]
&(ト)& 導 通 &(チ)& 283 &(リ)& 270 \\[ 5pt ]
&(ヌ)& 30 &(ル)& 120 \ [°] &(ヲ)& 逆阻止 \\[ 5pt ]
&(ワ)& 重なり角 &(カ)& 導通角 &(ヨ)& 50 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三相ブリッジダイオード整流器に関する問題です。
しっかりとメカニズムや図1-1の波形を理解していないと解けない問題となります。
さらに,本問では図2の交流リアクトルを接続した場合の計算も必要となります。本問(5)は他の問題を終了した後に取り組むか捨ててしまっても良いレベルかと思います。
1.三相ブリッジダイオード整流器の動作
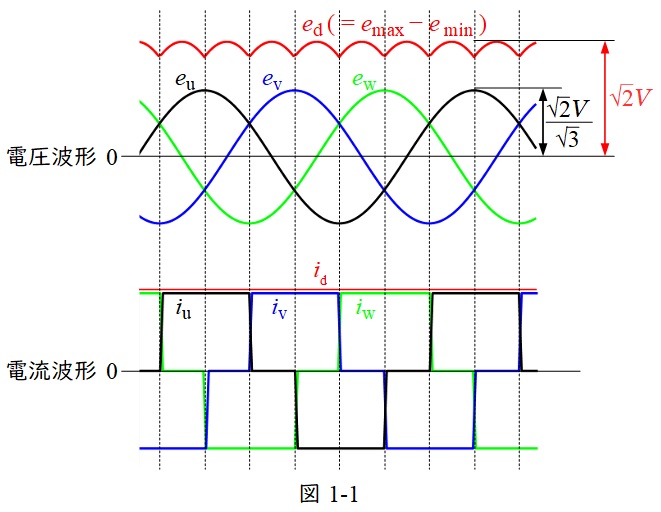
図1-1において,\( \ V \ \)が線間電圧,\( \ e_{\mathrm {u}} \ \),\( \ e_{\mathrm {v}} \ \),\( \ e_{\mathrm {w}} \ \),\( \ i_{\mathrm {u}} \ \),\( \ i_{\mathrm {v}} \ \),\( \ i_{\mathrm {w}} \ \)が各相の相電圧と電流,\( \ e_{\mathrm {d}} \ \),\( \ i_{\mathrm {d}} \ \)が出力電圧と電流です。
出力電圧は最も高い電圧と最も低い電圧の電位差となり,電流は電圧が最も高いダイオードから最も低いダイオードに流れます。平滑用直流リアクトルが十分に大きい場合には,出力電流は一定となります。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ル
図1-1より通電期間は\( \ \displaystyle \frac{\pi}{3} \ \mathrm {[rad]} \ \)毎にダイオードが切り替わるので,通電期間は\( \ 120 \ [°] \ \)となります。
(2)解答:リ
出力電圧の平均値は図1-1の\( \ e_{\mathrm {d}} \ \)の平均値となる。線間電圧\( \ V \ \)とすると一周期分の電圧は,
\[
\begin{eqnarray}
e_{\mathrm {d}}&=&\sqrt {2}V\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となり,出力電圧は\( \ \displaystyle \frac{\pi}{3} \ \mathrm {[rad]} \ \)の周期であるので,出力平均値\( \ E_{\mathrm {d}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {d}}&=&\frac {1}{\displaystyle \frac {\pi }{3}} \int ^{\frac {\pi }{6}}_{-\frac {\pi }{6}}e_{\mathrm {d}} \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3}{\pi } \int ^{\frac {\pi }{6}}_{-\frac {\pi }{6}}\sqrt {2}V\cos \theta \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {2}V}{\pi }\left[ \sin \theta \right] ^{\frac {\pi }{6}}_{-\frac {\pi }{6}} \\[ 5pt ]
&=&\frac {3\sqrt {2}V}{\pi }\left\{ \sin \frac {\pi }{6}-\sin \left( -\frac {\pi }{6}\right) \right\} \\[ 5pt ]
&=&\frac {3\sqrt {2}V}{\pi }\left\{ \frac {1}{2}-\left( -\frac {1}{2}\right)\right\} \\[ 5pt ]
&=&\frac {3\sqrt {2}V}{\pi } \\[ 5pt ]
\end{eqnarray}
\]
となる。これに\( \ V=200 \ \mathrm {[V]} \ \)を代入すると,
\[
\begin{eqnarray}
E_{\mathrm {d}}&=&\frac {3\sqrt {2}\cdot 200}{\pi } \\[ 5pt ]
&≒&270 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヲ
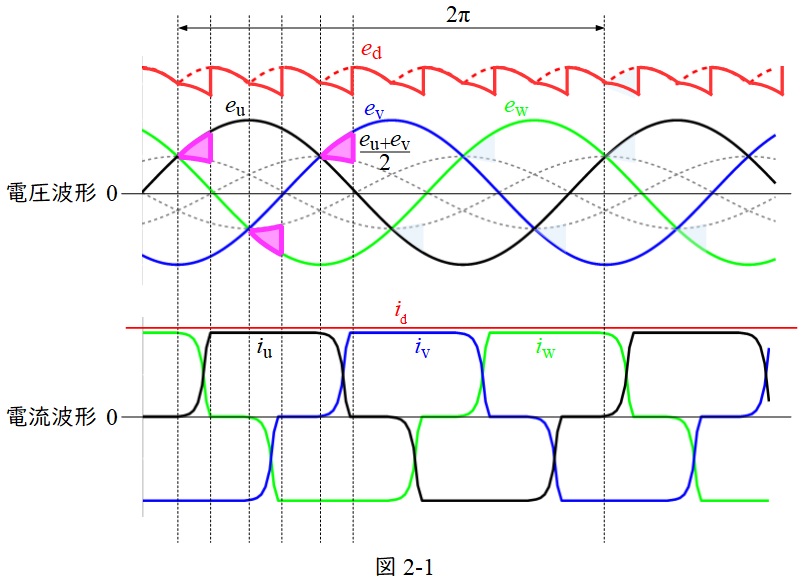
図2のように交流リアクトルを接続することにより,出力波形は図2-1のようになり,各ダイオードが切り替わるタイミング,即ち逆阻止状態になる時刻が遅くなります。
(4)解答:ワ
(3)の角度を転流の重なり角といいます。
(5)解答:ヌ
図2-1において,色塗りで示した部分内の微小区間での電流変化を\( \ \displaystyle \frac {\mathrm {d}i}{\mathrm {d}t} \ \)とすると,その時のリアクタンス降下は,
\[
\begin{eqnarray}
X \frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
となる。ただし,\( \ X=2\pi fL \ \)。
本問では周期\( \ \displaystyle \frac {\pi}{3} \ \)の間に\( \ 1 \ \)回のリアクタンス降下があるので,リアクタンス降下の平均値\( \ \Delta E_{\mathrm {d}} \ \)は,
\[
\begin{eqnarray}
\Delta E_{\mathrm {d}}&=&\frac {1}{\displaystyle \frac {\pi }{3}}\int X\frac {\mathrm {d}i}{\mathrm {d}t}\mathrm {d}t \\[ 5pt ]
&=&\frac {3}{\pi }\int ^{i_{\mathrm {d}}}_{0}2\pi fL\mathrm {d}i \\[ 5pt ]
&=&6fL\int ^{i_{\mathrm {d}}}_{0} \mathrm {d}i \\[ 5pt ]
&=&6fLi_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
上式に,\( \ f=50 \ \mathrm {[Hz]} \ \),\( \ L=1 \ \mathrm {[mH]} \ \),\( \ i_{\mathrm {d}}=100 \ \mathrm {[A]} \ \)を代入すると,
\[
\begin{eqnarray}
\Delta E_{\mathrm {d}} \\[ 5pt ]
&=&6fLi_{\mathrm {d}} \\[ 5pt ]
&=&6\times 50\times 1\times 10^{-3}\times 100 \\[ 5pt ]
&=&30 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん