【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,メカトロニクスのセンサに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
メカトロニクス分野で多用されている圧力センサとして,ストレインゲージが挙げられる。これは,素子のひずみで抵抗値が変化することを利用したセンサである。
ストレインゲージは,次のような特徴をもつ\( \ \mathrm {2} \ \)種類の素子で分類される。特に抵抗変化率\( \ \displaystyle \frac {\Delta R}{R} \ \)のひずみ\( \ \varepsilon \ \)に対する比\( \ \displaystyle K\left( =\frac {\Delta R / R}{\varepsilon } \right) \ \)は\( \ \fbox { (1) } \ \)と呼ばれ,この値はストレインゲージの素子によって大きく異なる。
金属ストレインゲージ:
ひずみが発生すると,金属の長さが変化し,素子の電気抵抗が変化する性質を利用したものである。上記の\( \ K \ \)が\( \ \mathrm {2} \ \)程度であり,抵抗の変化量が小さい。
\( \ \fbox { (2) } \ \)ストレインゲージ:
ひずみが発生すると,キャリア密度や移動度が変化する\( \ \fbox { (3) } \ \)によって素子特性そのものの抵抗率が変化する性質を利用しており,\( \ K \ \)も\( \ \mathrm {100~300} \ \)と大きく,広く普及してきている。また,この電気抵抗の温度特性は,金属と異なり,温度が高くなると電気抵抗が\( \ \fbox { (4) } \ \)なる性質がある。
これらのひずみゲージの微小な抵抗変化を測定するため,一般的には,測定抵抗を含んで四つの抵抗をブリッジ状に配置して,中間点の電位差を測定する\( \ \fbox { (5) } \ \)回路が利用される。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& 吸着効果 &(ロ)& 誘電体 &(ハ)& 膨張率 \\[ 5pt ]
&(ニ)& 高 く &(ホ)& はしご &(ヘ)& ピエゾ抵抗効果 \\[ 5pt ]
&(ト)& 拡散効果 &(チ)& 一定と &(リ)& 低 く \\[ 5pt ]
&(ヌ)& 磁性体 &(ル)& 半導体 &(ヲ)& 中 間 \\[ 5pt ]
&(ワ)& ホイートストンブリッジ &(カ)& 弾性率 &(ヨ)& ゲージ率 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ 2 \ \)種ではあまり出題されなかったメカトロニクス分野からの出題です。
ストレインゲージに関する問題ですが,多くの内容は理論科目の電気電子計測分野で出題される内容であるため,ストレインゲージの知識がなくてもある程度空欄を埋められる受験生も多かったのではないかと思います。
ストレインとは英語でひずみのことを意味し,日本語名ではひずみゲージとも呼ばれます。こちらの方が馴染みがある方もいるかもしれません。
1.ストレインゲージを利用した抵抗変化測定
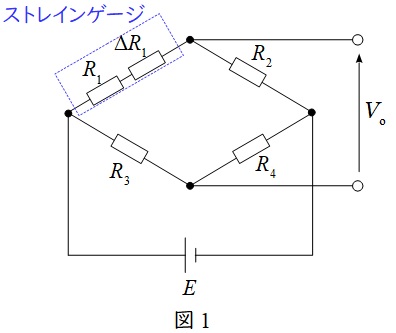
図1のように,素子のひずみにより微小な抵抗変化\( \ \Delta R_{1} \)を生じること(ピエゾ抵抗効果)を利用し,ホイートストンブリッジの原理を用いて測定します。
図1において,出力電圧\( \ V_{\mathrm {o}} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
V_{\mathrm {o}}&=&\frac {R_{2}}{\left( R_{1}+\Delta R_{1}\right) +R_{2}}E-\frac {R_{4}}{R_{3}+R_{4}}E \\[ 5pt ]
&=&\frac {R_{2}\left( R_{3}+R_{4}\right) -R_{4}\left\{ \left( R_{1}+\Delta R_{1}\right) +R_{2}\right\} }{\left\{ \left( R_{1}+\Delta R_{1}\right) +R_{2}\right\} \left( R_{3}+R_{4}\right) }E \\[ 5pt ]
\end{eqnarray}
\]
となります。ここで,\( \ R_{1}=R_{2}=R_{3}=R_{4}=R \ \)と設定すれば,
\[
\begin{eqnarray}
V_{\mathrm {o}}&=&\frac {R\left( R+R\right) -R\left\{ \left( R+\Delta R\right) +R\right\} }{\left\{ \left( R+\Delta R\right) +R\right\} \left( R+R\right) }E \\[ 5pt ]
&=&\frac {2R^{2} -R\left( 2R+\Delta R\right) }{\left( 2R+\Delta R\right) \cdot 2R}E \\[ 5pt ]
&=&\frac {\Delta R }{4R+2\Delta R}E \\[ 5pt ]
\end{eqnarray}
\]
となります。ここで,\( \ R≫\Delta R \ \)と考えると,
\[
\begin{eqnarray}
V_{\mathrm {o}}&≃&\frac {\Delta R }{4R}E \\[ 5pt ]
\end{eqnarray}
\]
となり,ひずみ\( \ \varepsilon \ \)に対する比であるゲージ率\( \ \displaystyle K\left( =\frac {\Delta R/R}{\varepsilon }\right) \ \)を用いて表すと,
\[
\begin{eqnarray}
V_{\mathrm {o}}&=&\frac {K}{4}\varepsilon E \\[ 5pt ]
\end{eqnarray}
\]
で表すことができます。
【解答】
(1)解答:ヨ
題意より解答候補は,(ハ)膨張率,(カ)弾性率,(ヨ)ゲージ率,になると思います。
ワンポイント解説「1.ストレインゲージを利用した抵抗変化測定」でも触れていますが,\( \ \displaystyle K\left( =\frac {\Delta R / R}{\varepsilon } \right) \ \)はゲージ率と呼ばれます。
(2)解答:ル
題意より解答候補は,(ロ)誘電体,(ヌ)磁性体,(ル)半導体,になると思います。
ストレインゲージには,金属ストレインゲージの他に半導体ストレインゲージがあります。説明文に「キャリヤ密度や移動度が変化する」と記載があることからも,半導体が選択できるかと思います。
(3)解答:ヘ
題意より解答候補は,(イ)吸着効果,(ヘ)ピエゾ抵抗効果,(ト)拡散効果,になると思います。
ワンポイント解説「1.ストレインゲージを利用した抵抗変化測定」の通り,ひずみが発生するとキャリヤ密度や移動度が変化する,すなわち抵抗率が変化する性質をピエゾ抵抗効果といいます。
(4)解答:リ
題意より解答候補は,(ニ)高く,(チ)一定と,(リ)低く,になると思います。
半導体では,温度が高くなると,生成される電子正孔対(キャリヤ)が増加するため,電流が流れやすくなります。したがって,電気抵抗は低くなります。
(5)解答:ワ
題意より解答候補は,(ホ)はしご,(ヲ)中間,(ワ)ホイートストンブリッジ,になると思います。
四つの抵抗をブリッジ状に配置,すなわち図1のように配置することをホイートストンブリッジ回路といいます。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん