《機械》〈回転機〉[H30:問1]同期発電機の電機子巻線の分布係数に関する計算・空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，同期発電機の電機子巻線の分布係数に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

同期発電機では界磁磁束によって電機子巻線に発生する誘導起電力の波形は正弦波であることが望ましい。しかし，界磁磁束の空隙の磁束密度分布は台形波に近くなり，$ \ \fbox {　（１）　} \ $次の高調波成分を含む。また，電機子巻線に対称三相交流電流が流れるとき，$ \ 1 \ $個のコイルによって生じる回転方向に沿った起磁力の分布は$ \ \fbox {　（２）　} \ $波となり，$ \ \fbox {　（１）　} \ $次の高調波成分を含む。そこで界磁磁束によって電機子巻線に発生する誘導起電力の波形を正弦波に近づけるとともに，電機子電流による起磁力の高調波成分を低減するため，電機子巻線に分布巻が用いられる。ここでは，界磁磁束によって電機子巻線に発生する誘導起電力の波形に対する分布巻の効果を分布係数で説明する。

毎極毎相の導体を$ \ 1 \ $個のスロットに納める集中巻に対して，何個かのスロットに分布して配置することを分布巻という。毎極毎相のスロット数を$ \ q \ $個(整数とする)とすると，隣り合うコイルの誘導起電力はスロット間隔に対応した位相差を生じ，$ \ q \ $個のコイルに発生する誘導起電力は各コイルの誘導起電力の$ \ \fbox {　（３）　} \ $となる。一方，集中巻の場合は$ \ 1 \ $個のコイルの誘導起電力の大きさの$ \ q \ $倍となる。

分布巻の場合の集中巻の場合に対する誘導起電力の大きさの比を分布係数という。相数を$ \ m \ $として，基本波成分に対してはスロット間隔に対応して各コイルの位相差は電気角で$ \ \displaystyle \alpha =\frac {\pi }{mq} \ \mathrm {[rad]} \ $となり，分布係数は$ \ k_{\mathrm {d1}}=\fbox {　（４）　} \ $となる。また，$ \ \nu \ $次高調波成分に対してはスロット間隔に対応して隣り合うコイルの高調波誘導起電力の位相差は電気角で$ \ \displaystyle \nu \alpha =\frac {\nu \pi }{mq} \ \mathrm {[rad]} \ $となるので，$ \ \nu \ $次高調波誘導起電力に対する分布係数は$ \ k_{\mathrm {d\nu }}=\fbox {　（５）　} \ $となる。

分布係数の値は，通常，基本波に対しては数パーセントの減少であるが，高調波に対しては大きな減少となり，誘導起電力の波形は正弦波に近づく。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　偶数　　　　　&（ロ）&　奇数　　　　　&（ハ）&　\frac {\displaystyle \sin \left( \frac {\pi }{2m}\right) }{\displaystyle q\sin \left( \frac {\pi }{2mq}\right) } \\[ 5pt ] &（ニ）&　三角　　　　　&（ホ）&　\frac {\displaystyle \cos \left( \frac {\pi }{m}\right) }{\displaystyle q\cos \left( \frac {\pi }{mq}\right) }　　　&（ヘ）&　のこぎり \\[ 5pt ] &（ト）&　方形　　　　　&（チ）&　\frac {\displaystyle \sin \left( \frac {\nu \pi }{2m}\right) }{\displaystyle q\sin \left( \frac {\nu \pi }{2mq}\right) }　　　&（リ）&　ベクトル積 \\[ 5pt ] &（ヌ）&　分数　　　　　&（ル）&　\frac {\displaystyle \sin \left( \frac {\nu \pi }{m}\right) }{\displaystyle q\sin \left( \frac {\nu \pi }{mq}\right) }　　　&（ヲ）&　\frac {\displaystyle \sin \left( \frac {\pi }{m}\right) }{\displaystyle q\sin \left( \frac {\pi }{mq}\right) } \\[ 5pt ] &（ワ）&　代数和　　　　　&（カ）&　\frac {\displaystyle \cos \left( \frac {\nu \pi }{m}\right) }{\displaystyle q\cos \left( \frac {\nu \pi }{mq}\right) }　　　　　&（ヨ）&　ベクトル和 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

一問目から難しい問題です。多くの受験生が勘に頼って回答したと思います。平成27年の電験二種機械問5に類題が出題されていますが，この問題はさらに高度にしたような問題と言えます。

1.集中巻と分布巻
集中巻は，電機子巻線を一つのスロットに集中して巻き付ける巻線方式で，奇数次の高調波を含むことにより，ギャップの磁束密度の分布がほぼ台形に近い形になってしまい，起電力もひずみ波になってしまいます。一方，分布巻は電機子巻線を二つ以上のスロットに巻き付ける巻線方式で，ギャップの磁束密度の分布をより正弦波に近い形にしようとする巻線方式です。発電機で使用されているのは分布巻となります。

出典：三菱電機株式会社　ＨＰ
https://www.mitsubishielectric.co.jp/

【解答】

(1)解答：ロ
題意より，解答候補は（イ）偶数，（ロ）奇数，（ヌ）分数，となると思います。界磁磁束の空隙の磁束密度分布は台形波に近くなり，奇数次の高調波成分を含みます。奇数次の高調波を含むとフーリエ解析で計算すればわかりますが，次数が増えれば増えるほど台形の波形に近づいていきます。

(2)解答：ト
題意より，解答候補は（ニ）三角，（ヘ）のこぎり，（ト）方形，となると思います。起磁力の分布は方形波となりますが，知識として知らなくても「奇数次の高調波成分を含む」と問題文に記載があるため，そこから方形波と導き出すことができます。

(3)解答：ヨ
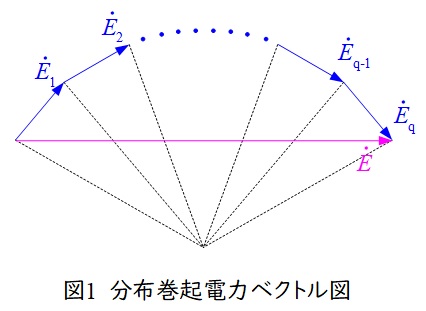
題意より，解答候補は（リ）ベクトル積，（ワ）代数和，（ヨ）ベクトル和，となると思います。分布巻の誘導起電力は図1に示すように，各コイルの誘導起電力のベクトル和となります。

(4)解答：ハ
集中巻の起電力$ \ E_{\mathrm {c}} \ $は，各コイルの誘導起電力のスカラー和となる。したがって，
\[
\begin{eqnarray}
E_{\mathrm {c}} &=&E_{1}+E_{2}+\cdots +E_{\mathrm {q-1}}+E_{\mathrm {q}} \\[ 5pt ] &=&qE_{1} \\[ 5pt ] \end{eqnarray}
\] となる。ただし，$ \ E_{1} \ $はベクトル$ \ {\dot E}_{1} \ $の大きさである。
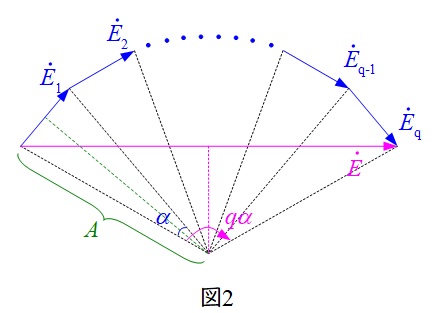
分布巻については，図2のように，起電力ベクトル図に補助線を引き，線分$ \ A \ $を図2のようにおくと，
\[
\begin{eqnarray}
A\sin \frac {\alpha }{2} &=&\frac {E_{1}}{2}　　&・・・・・・・・・・①& \\[ 5pt ] A\sin \frac {q\alpha }{2} &=&\frac {E}{2}　　&・・・・・・・・・・②& \\[ 5pt ] \end{eqnarray}
\] の関係があるから，$①÷②$を$ \ E \ $について整理すると，
\[
\begin{eqnarray}
\frac {\displaystyle \sin \frac {\alpha }{2}}{\displaystyle \sin \frac {q\alpha }{2}} &=&\frac {E_{1}}{E} \\[ 5pt ] E &=&\frac {\displaystyle \sin \frac {q\alpha }{2}}{\displaystyle \sin \frac {\alpha }{2}}E_{1} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，$ \ \displaystyle \alpha =\frac {\pi }{mq} \ \mathrm {[rad]} \ $を代入すると，
\[
\begin{eqnarray}
E &=&\frac {\displaystyle \sin \frac {\pi }{2m}}{\displaystyle \sin \frac {\pi }{2mq}}E_{1} \\[ 5pt ] &=&\frac {\displaystyle \sin \frac {\pi }{2m}}{\displaystyle q\sin \frac {\pi }{2mq}}E_{\mathrm {c}} \\[ 5pt ] \end{eqnarray}
\] となり，
\[
\begin{eqnarray}
k_{\mathrm {d1}} &=&\frac {\displaystyle \sin \frac {\pi }{2m}}{\displaystyle q\sin \frac {\pi }{2mq}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：チ
$ \ \nu \ $次高調波成分に対しては上式の$ \ \alpha \ $を$ \ \nu \alpha \ $に置き換えれば良いので，
\[
\begin{eqnarray}
k_{\mathrm {d\nu }} &=&\frac {\displaystyle \sin \frac {\nu \pi }{2m}}{\displaystyle q\sin \frac {\nu \pi }{2mq}} \\[ 5pt ] \end{eqnarray}
\] と求められる。