《電力》〈送電〉[H23:問5] 送電端と受電端における電圧の関係に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，送電端と受電端における電圧の関係に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

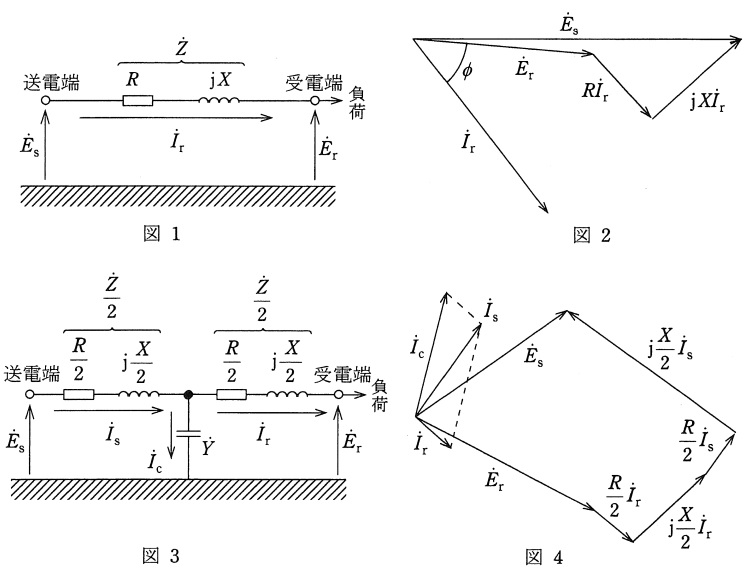
送電線路のこう長が短く，静電容量を無視でき，等価的に図1のように表される送電系統について考える。一般の負荷は遅れ力率であることが多いため，受電端の負荷が大きいときの電圧，電流ベクトルは図2のようになり，送電端電圧よりも受電端電圧が低くなる。ここで，線路が非常に短く送電端と受電端の間の$ \ \fbox {　（１）　} \ $が無視できるほど小さいとすると，$ \ E_{\mathrm {s}}=\fbox {　（２）　} \ $と近似計算できる。図1において，$ \ R=0.02 \ [\mathrm {p.u.}] \ $，$ \ X=0.4 \ [\mathrm {p.u.}] \ $，$ \ E_{\mathrm {r}}=1.0 \ [\mathrm {p.u.}] \ $，$ \ I_{\mathrm {r}}=0.7 \ [\mathrm {p.u.}] \ $，$ \ \cos \phi =1.0 \ $とすると，送電端電圧の近似式$ \ \fbox {　（２）　} \ $による計算では$ \ \fbox {　（３）　} \ [\mathrm {p.u.}] \ $の誤差を生じる。

次に，送電線路のこう長が長く，静電容量が無視できず，等価的に図3のように表される送電系統について考える。このとき，送電線電流と電圧のベクトルはそれぞれ，$ \ \dot I_{\mathrm {s}}= \ \fbox {　（４）　} \ $，$ \ \dot E_{\mathrm {s}}= \ \fbox {　（５）　} \ $となり，ベクトル図で表すと図4のようになる。図4では受電端電圧は送電端電圧より高くなっており，このような現象を$ \ \fbox {　（６）　} \ $という。

図3において，$ \ R=0.0 \ [\mathrm {p.u.}] \ $，$ \ X=0.4 \ [\mathrm {p.u.}] \ $，$ \ Y=0.2 \ [\mathrm {p.u.}] \ $，$ \ E_{\mathrm {s}}=1.0 \ [\mathrm {p.u.}] \ $とし，受電端から負荷に進み無効電流$ \ 0.1 \ [\mathrm {p.u.}] \ $が流れ出ているとすると受電端電圧$ \ E_{\mathrm {r}} \ $は送電端電圧$ \ E_{\mathrm {s}} \ $よりも$ \ \fbox {　（７）　} \ [\mathrm {p.u.}] \ $高くなる。ここで受電端電圧を$ \ 1.0 \ [\mathrm {p.u.}] \ $にするためには$ \ \fbox {　（８）　} \ [\mathrm {p.u.}] \ $のアドミタンスを持つ分路リアクトルを受電端に投入する必要がある。
ただし，$ \ \cos \phi \ $は受電端の力率を，図中の記号は以下のとおりのものを表し，送電線路の漏れコンダクタンスは無視するものとする。

$・\dot E_{\mathrm {s}} \ $：送電端相電圧　$・\dot E_{\mathrm {r}} \ $：受電端相電圧
$・\dot I_{\mathrm {s}} \ $：送電端電流　　$・\dot I_{\mathrm {r}} \ $：受電端電流　$・\dot I_{\mathrm {c}} \ $：静電容量に流れる電流
$・\dot Z=R+\mathrm {j}X \ $：電線$ \ 1 \ $条の全インピーダンス
　($ \ R \ $：電線$ \ 1 \ $条の全抵抗，$ \ X \ $：電線1条の全リアクタンス)
$・\dot Y \ $：電線$ \ 1 \ $条の全並列アドミタンス

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　\dot Z \dot Y \dot I_{\mathrm {r}}+\dot E_{\mathrm {r}}\dot Y　　　&（ロ）&　E_{\mathrm {r}}+\left( R\sin \phi +X\cos \phi \right)I_{\mathrm {r}} \\[ 5pt ] &（ハ）&　0.083　　　&（ニ）&　無効電力損失 \\[ 5pt ] &（ホ）&　キャパシタンス効果　　　&（ヘ）&　\dot I_{\mathrm {r}}+\dot E_{\mathrm {r}}\dot Y \\[ 5pt ] &（ト）&　フェランチ効果　　　&（チ）&　無効電力効果 \\[ 5pt ] &（リ）&　有効電力損失　　　&（ヌ）&　\left( 1+\frac {\dot Z \dot Y}{2}\right) \dot I_{\mathrm {r}}+\dot E_{\mathrm {r}} \dot Y \\[ 5pt ] &（ル）&　E_{\mathrm {r}}+\left( R\cos \phi +X\sin \phi \right)I_{\mathrm {r}}　　　&（ヲ）&　0.18 \\[ 5pt ] &（ワ）&　電圧位相差　　　&（カ）&　0.22 \\[ 5pt ] &（ヨ）&　0.20　　　&（タ）&　\left( 1+\dot Z \dot Y\right)\dot E_{\mathrm {r}}+\dot Z\left( 1+\dot Z \dot Y\right) \dot I_{\mathrm {r}} \\[ 5pt ] &（レ）&　0.051　　　&（ソ）&　0.026 \\[ 5pt ] &（ツ）&　0.038　　　&（ネ）&　\left( 1+\frac{\dot Z \dot Y}{2}\right)\dot E_{\mathrm {r}}+\dot Z\left( 1+\frac{\dot Z \dot Y}{4}\right)\dot I_{\mathrm {r}}
\end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {T} \ $形等価回路を使用した送電線の電圧に関する問題です。
$ \ 1 \ $種の二次試験ではさらに計算量を多くした問題が出題されます。$ \ \pi \ $形回路と合わせて理解しておきましょう。

【解答】

(1)解答：ワ
解答候補は（ニ）無効電力損失，（リ）有効電力損失，（ワ）電圧位相差，になると思います。
$ \ \dot Z=R+\mathrm {j}X \ $で有効電力損失も無効電力損失も考慮しており，電圧降下の近似計算に関する内容として最も適当なのは電圧位相差となります。

(2)解答：ル
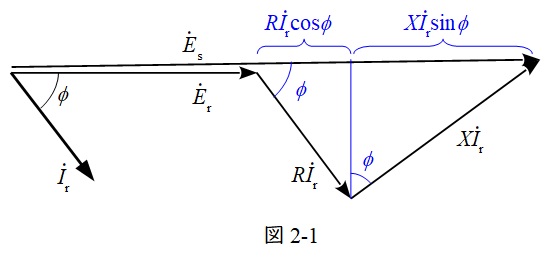
電圧位相差がないと仮定すると図2のベクトル図は図2-1のように描くことができる。図の2-1より
\[
\begin{eqnarray}
E_{\mathrm {s}}&=&E_{\mathrm {r}}+RI_{\mathrm {r}}\cos \phi +XI_{\mathrm {r}}\sin \phi \\[ 5pt ] &=&E_{\mathrm {r}}+\left( R\cos \phi +X\sin \phi \right)I_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ツ
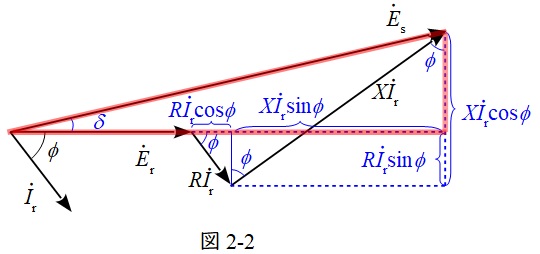
送電端と受電端の位相差は無視できないとしてベクトル図を記載すると図2-2となる。
図2-2の赤線で示す三角形において，三平方の定理を適用すると，
\[
\begin{eqnarray}
E^{2}_{\mathrm {s}}&=&\left( E_{\mathrm {r}}+RI_{\mathrm {r}}\cos \phi +XI_{\mathrm {r}}\sin \phi \right) ^{2}+\left( XI_{\mathrm {r}}\cos \phi -RI_{\mathrm {r}}\sin \phi \right) ^{2} \\[ 5pt ] E_{\mathrm {s}}&=&\sqrt {\left( E_{\mathrm {r}}+RI_{\mathrm {r}}\cos \phi +XI_{\mathrm {r}}\sin \phi \right) ^{2}+\left( XI_{\mathrm {r}}\cos \phi -RI_{\mathrm {r}}\sin \phi \right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ R=0.02 \ [\mathrm {p.u.}] \ $，$ \ X=0.4 \ [\mathrm {p.u.}] \ $，$ \ E_{\mathrm {r}}=1.0 \ [\mathrm {p.u.}] \ $，$ \ I_{\mathrm {r}}=0.7 \ [\mathrm {p.u.}] \ $，$ \ \cos \phi =1.0 \ $，$ \ \sin \phi =0 \ $を代入すると，
\[
\begin{eqnarray}
E_{\mathrm {s}}&=&\sqrt {\left( 1.0+0.02\times 0.7\times 1.0 +0.4\times 0.7\times 0 \right) ^{2}+\left( 0.4\times 0.7\times 1.0 -0.02\times 0.7\times 0 \right) ^{2}} \\[ 5pt ] &=&\sqrt {1.014 ^{2}+0.28 ^{2}} \\[ 5pt ] &≒&1.052 \\[ 5pt ] \end{eqnarray}
\] となる。一方，(2)の解答式に各値を代入すると，
\[
\begin{eqnarray}
E_{\mathrm {s}}&=&1.0+\left( 0.02\times 1.0 +0.4\times 0 \right)\times 0.7 \\[ 5pt ] &=&1.014 \\[ 5pt ] \end{eqnarray}
\] となる。ゆえに，$ \ 1.052-1.014=0.038 \ [\mathrm {p.u.}] \ $の誤差が生じる。

(4)解答：ヌ
図3において，中間点の電圧を$ \ \dot E_{\mathrm {m}} \ $とすると，
\[
\begin{eqnarray}
\dot E_{\mathrm {m}}&=&\frac {\dot Z}{2}\dot I_{\mathrm {r}}+\dot E_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] となるので，中間点のコンデンサを流れる電流$ \ \dot I_{\mathrm {c}} \ $は，
\[
\begin{eqnarray}
\dot I_{\mathrm {c}}&=&\dot E_{\mathrm {m}}\dot Y \\[ 5pt ] &=&\left( \frac {\dot Z}{2}\dot I_{\mathrm {r}}+\dot E_{\mathrm {r}}\right)\dot Y \\[ 5pt ] &=&\frac {\dot Z \dot Y}{2}I_{\mathrm {r}}+\dot E_{\mathrm {r}}\dot Y \\[ 5pt ] \end{eqnarray}
\] となり，送電端から流れる電流$ \ \dot I_{\mathrm {s}} \ $は，
\[
\begin{eqnarray}
\dot I_{\mathrm {s}}&=&\dot I_{\mathrm {c}}+\dot I_{\mathrm {r}} \\[ 5pt ] &=&\frac {\dot Z \dot Y}{2}I_{\mathrm {r}}+\dot E_{\mathrm {r}}\dot Y+\dot I_{\mathrm {r}} \\[ 5pt ] &=&\left( 1+\frac {\dot Z \dot Y}{2}\right)I_{\mathrm {r}}+\dot E_{\mathrm {r}}\dot Y \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ネ
送電端電圧$ \ \dot E_{\mathrm {s}} \ $は，
\[
\begin{eqnarray}
\dot E_{\mathrm {s}}&=&\frac {\dot Z}{2}\dot I_{\mathrm {s}}+\dot E_{\mathrm {m}} \\[ 5pt ] &=&\frac {\dot Z}{2}\left\{ \left( 1+\frac {\dot Z \dot Y}{2}\right)\dot I_{\mathrm {r}}+\dot E_{\mathrm {r}}\dot Y\right\} +\frac {\dot Z}{2}\dot I_{\mathrm {r}}+\dot E_{\mathrm {r}} \\[ 5pt ] &=& \frac {\dot Z}{2}\dot I_{\mathrm {r}}+\frac {\dot Z}{2}\cdot \frac {\dot Z \dot Y}{2}\dot I_{\mathrm {r}}+\frac {\dot Z \dot Y}{2}\dot E_{\mathrm {r}} +\frac {\dot Z}{2}\dot I_{\mathrm {r}}+\dot E_{\mathrm {r}} \\[ 5pt ] &=&\left( 1+\frac{\dot Z \dot Y}{2}\right)\dot E_{\mathrm {r}}+\dot Z\left( 1+\frac{\dot Z \dot Y}{4}\right)\dot I_{\mathrm {r}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(6)解答：ト
夜間軽負荷時等に受電端電圧が送電端電圧より高くなる現象をフェランチ効果といいます。

(7)解答：ハ
題意より，$ \ \dot E_{\mathrm {r}} \ $を基準ベクトルとすると，
\[
\begin{eqnarray}
\dot Z&=&R+\mathrm {j}X \\[ 5pt ] &=&\mathrm {j}0.4 \ [\mathrm {p.u.}] \\[ 5pt ] \dot Y&=&\mathrm {j}0.2 \ [\mathrm {p.u.}] \\[ 5pt ] \dot I_{\mathrm {r}}&=&\mathrm {j}0.1 \ [\mathrm {p.u.}] \\[ 5pt ] \end{eqnarray}
\] となるから(5)解答式は，
\[
\begin{eqnarray}
\dot E_{\mathrm {s}}&=&\left( 1+\frac{\dot Z \dot Y}{2}\right)\dot E_{\mathrm {r}}+\dot Z\left( 1+\frac{\dot Z \dot Y}{4}\right)\dot I_{\mathrm {r}} \\[ 5pt ] &=&\left( 1+\frac {\mathrm {j}0.4\times \mathrm {j}0.2}{2}\right) E_{\mathrm {r}}+\mathrm {j}0.4 \left( 1+\frac {\mathrm {j}0.4\times \mathrm {j}0.2}{4}\right)\times \mathrm {j}0.1 \\[ 5pt ] &=&0.96 E_{\mathrm {r}}-0.0392 \\[ 5pt ] \end{eqnarray}
\] となり，虚数部がなくなるので，$ \ \dot E_{\mathrm {s}} \ $と$ \ \dot E_{\mathrm {r}} \ $は同相となる。したがって，$ \ \dot E_{\mathrm {s}}=1.0 \ [\mathrm {p.u.}] \ $を代入すると，
\[
\begin{eqnarray}
1.0&=&0.96 E_{\mathrm {r}}-0.0392 \\[ 5pt ] E_{\mathrm {r}}&=&1.0825 \\[ 5pt ] \end{eqnarray}
\] と求められ，$ \ E_{\mathrm {r}} \ $の方が$ \ E_{\mathrm {s}} \ $よりも$ \ 0.0825≒0.083 \ [\mathrm {p.u.}] \ $高くなる。

(8)解答：ヨ
分路リアクトルを挿入することによって受電端電圧の位相変化は発生しないため，本題においても$ \ \dot E_{\mathrm {s}} \ $と$ \ \dot E_{\mathrm {r}} \ $は同相となる。
したがって，$ \ E_{\mathrm {s}}=E_{\mathrm {r}}=1.0 \ $及び$ \ Z=\mathrm {j}0.4 \ $,$ \ Y=\mathrm {j}0.2 \ $を(5)解答に代入すると，
\[
\begin{eqnarray}
1.0&=&0.96 \times 1.0 +\mathrm {j}0.392 I_{\mathrm {r}} \\[ 5pt ] ∴　I_{\mathrm {r}}&=&-\mathrm {j}0.102 \\[ 5pt ] \end{eqnarray}
\] よって，分路リアクトルが消費する進み無効電流は，
\[
\begin{eqnarray}
\mathrm {j}0.1-\left( -\mathrm {j}0.102\right)&=&\mathrm {j}0.202 \\[ 5pt ] \end{eqnarray}
\] となる。したがって，分路リアクトルのアドミタンス$ \ Y_{\mathrm {L}} \ $は，
\[
\begin{eqnarray}
Y_{\mathrm {L}}&=&\frac {\mathrm {j}0.202}{1.0} \\[ 5pt ] &≒&\mathrm {j}0.20 \ [\mathrm {p.u.}] \\[ 5pt ] \end{eqnarray}
\] と求められる。