【問題】
【難易度】★☆☆☆☆(易しい)
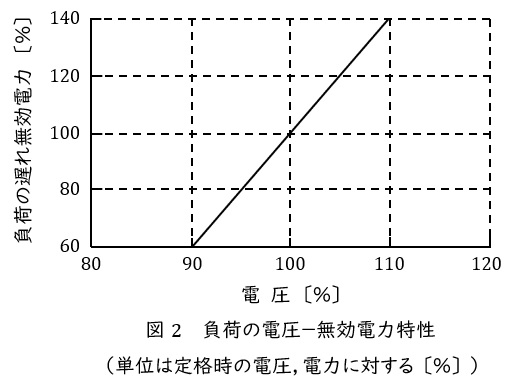
図1の電力系統において,系統の末端電圧\( \ V_{\mathrm {r}} \ \)は,負荷の遅れ無効電力\( \ Q \ \)に対して①式の直線特性で降下するものと仮定する。この系統の末端に接続される負荷の遅れ無効電力が,端子電圧に対して図2のような直線特性があるとすれば,系統の末端における電圧と無効電力は,ある値で安定状態となる。
系統のリアクタンス\( \ X \ \)は,\( \ 5.0 \ \mathrm {[%]} \ \)(\( \ 100 \ \mathrm {[MV\cdot A]} \ \)基準\(%\))で一定であり,定格電圧時の負荷の遅れ無効電力が\( \ 50 \ \mathrm {[MV\cdot A]} \ \)であるとき,安定状態における系統の末端電圧\( \ \mathrm {[p.u.]} \ \)及び負荷の無効電力\( \ \mathrm {[MV\cdot A]} \ \)を求めよ。なお,電圧降下において負荷の有効電力及び送電系統の抵抗分は無視できるものとし,系統の送電端電圧\( \ V_{\mathrm {s}} \ \)は\( \ 1.0 \ \mathrm {[p.u.]} \ \)(\( = \)定格電圧)で一定であるものとする。

\[
\begin{eqnarray}
系統の電圧特性:V_{\mathrm {r}}=V_{\mathrm {s}}-X\cdot Q ・・・①式 \\[ 5pt ]
\left\{
\begin{array}{l}
V_{\mathrm {r}}&:&系統の末端電圧 \ \mathrm {[p.u.]} \\
V_{\mathrm {s}}&:&系統の送電端電圧 \ \mathrm {[p.u.]} \\
X&:&系統のリアクタンス \ \mathrm {[p.u.]} \\
Q&:&負荷の遅れ無効電力 \ \mathrm {[p.u.]} \\
\end{array}
\right.
\end{eqnarray}
\]
【ワンポイント解説】
安定状態となったときの系統の末端における電圧と無効電力を求める問題です。
難易度的には易しい問題ですが,問題文を読み解いた上で計算間違いに注意して解く必要があります。小さなミスが大きな減点に繋がるので,十分に注意して解くようにして下さい。
1.オーム法から単位法への変換
基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)の時,インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)を単位法で表すと,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ [\Omega ] \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}} (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.単位法における容量換算
「1.オーム法から単位法への変換」の通り,単位法のインピーダンスは基準容量に比例します。したがって,基準容量\( \ P_{\mathrm {A}} \ \)から\( \ P_{\mathrm {B}} \ \)へ変換する場合の単位法におけるインピーダンスは,
\[
\begin{eqnarray}
Z_{\mathrm {B}} \ \mathrm {[p.u.]}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}Z_{\mathrm {A}} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
図2における特性直線について,傾きは電圧が\( \ 10 \ \mathrm {[%]} \ \)増えるごとに負荷の無効電力が\( \ 40 \ \mathrm {[%]} \ \)増えているから\( \ 4 \ \)であり,切片を\( \ b \ \)とすれば,\( \ Q=4V_{\mathrm {r}}+b \ \)とおくことができる。図2より,\( \ V_{\mathrm {r}}=1 \ \mathrm {[p.u.]} \ \)のとき\( \ Q=1 \ \mathrm {[p.u.]} \ \)であるから,
\[
\begin{eqnarray}
1&=&4\times 1+b \\[ 5pt ]
b&=&-3 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,図2の負荷の電圧-無効電力特性は\( \ Q=4V_{\mathrm {r}}-3 \ \)となる。
これを①式に代入すれば,
\[
\begin{eqnarray}
V_{\mathrm {r}}&=&V_{\mathrm {s}}-X\cdot Q \\[ 5pt ]
&=&V_{\mathrm {s}}-X\cdot \left( 4V_{\mathrm {r}}-3\right) ・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,系統のリアクタンス\( \ X \ \)を\( \ 50 \ \mathrm {[MV\cdot A]} \ \)基準に換算した\( \ X_{50} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
X_{50}&=&\frac {50}{100}\times 0.05 \\[ 5pt ]
&=&0.025 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,これと\( \ V_{\mathrm {s}}=1.0 \ \mathrm {[p.u.]} \ \)を②式に代入すると,
\[
\begin{eqnarray}
V_{\mathrm {r}}&=&V_{\mathrm {s}}-X_{50}\cdot \left( 4V_{\mathrm {r}}-3\right) \\[ 5pt ]
V_{\mathrm {r}}&=&1.0-0.025\times \left( 4V_{\mathrm {r}}-3\right) \\[ 5pt ]
V_{\mathrm {r}}&=&1.0-0.1V_{\mathrm {r}}+0.075 \\[ 5pt ]
1.1V_{\mathrm {r}}&=&1.075 \\[ 5pt ]
V_{\mathrm {r}}&≒&0.97727 → 0.977 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,これを①式に代入すると,
\[
\begin{eqnarray}
V_{\mathrm {r}}&=&V_{\mathrm {s}}-X_{50}\cdot Q \\[ 5pt ]
0.97727&=&1.0-0.025\times Q \\[ 5pt ]
0.025Q &=&0.02273 \\[ 5pt ]
Q &=&0.9092 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,負荷の無効電力\( \ Q \ \mathrm {[MV\cdot A]} \ \)は,
\[
\begin{eqnarray}
Q&=&50\times 0.09092 \\[ 5pt ]
&≒&45.5 \ \mathrm {[MV\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん