【問題】
【難易度】★★★★★(難しい)
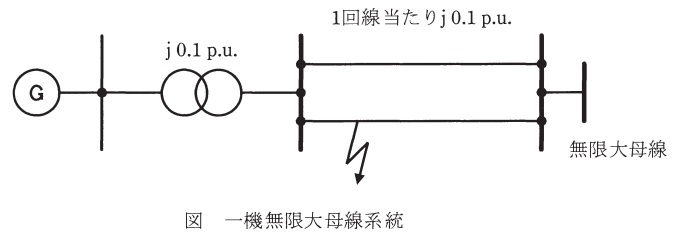
図において,並行\( \ 2 \ \)回線送電線(周波数\( \ \mathrm{50 \ Hz} \ \))の\( \ 1 \ \)回線故障に伴う高速再閉路がタービン発電機の軸に与える影響を検討する。昇圧変圧器の高圧側母線至近端で三相短絡故障(故障点抵抗零)が発生し,その後\( \ \mathrm{0.1} \ \)秒で三相遮断,故障除去,\( \ 1 \ \)回線運用に瞬時に移行した状況を想定している。次の問に答えよ。
タービン発電機は過渡リアクタンス背後電圧一定のモデルで表現し,その定格容量は\( \ \mathrm{1000 \ MV \cdot A} \ \),過渡リアクタンスは\( \ x_{\mathrm {d}}^{\prime } =0.3 \ \mathrm{p.u.} \ \)(自己容量基準),慣性定数\( \ M \ \)は自己容量基準で\( \ 7 \ \)秒とし,固定子抵抗,励磁制御や調速機の効果,電気的トルクの振動成分は全て無視するものとする。ここで,発電機の回転速度\( \ \omega \ \)の挙動は,機械的入力\( \ P_{\mathrm {m}} \ \),電気的出力\( \ P_{\mathrm {e}} \ \)を用いて,微分方程式
\[
\begin{eqnarray}
M\frac {\mathrm {d}\omega }{\mathrm {d}t}&=&P_{\mathrm {m}}-P_{\mathrm {e}} \\[ 5pt ]
\end{eqnarray}
\]
で表現するものとする。なお,回転速度の変化は小さいため,電力とトルクは同じものと仮定する。変圧器と送電線はともにリアクタンス\( \ 0.1 \ \mathrm{p.u.} \ \)(\( \ 1000 \ \mathrm{MV \cdot A} \ \)基準。送電線は\( \ 1 \ \)回線分)とし,その他のインピーダンスは無視する。故障発生前は,タービン発電機は定格端子電圧\( \ 1.0 \ \mathrm{p.u.} \ \),定格出力,定格力率\( \ 90 \ % \ \)(遅れ)で運転していたものとする。
(1) 短絡時の電気的トルクのステップ変化の大きさを\( \ \mathrm{p.u.} \ \)単位で求めよ。
(2) 故障発生後\( \ 0.1 \ \)秒間のタービン発電機の内部相差角増大量\( \ \Delta \delta \ \)を\( \ \mathrm{rad} \ \)単位で計算せよ。
(3) 故障発生前及び故障除去後(\( \ 1 \ \)回線運用中)の直列合成リアクタンス(発電機内部電圧から無限大母線までの間にある全リアクタンスを合成した値)をそれぞれ求めよ。また,故障発生前の発電機の運転条件から\( \ x_{\mathrm {d}}^{\prime } \ \)背後電圧\( \ \dot E_{\mathrm {q}}^{\prime } \ \)の大きさと,無限大母線電圧\( \ \dot V_{\mathrm {i}} \ \)の大きさを求めよ。答えは全て\( \ \mathrm{p.u.} \ \)単位で記すこと。
(4) 小問(2)で求めた故障除去時までの\( \ \Delta \delta \ [\mathrm{rad}] \ \)について\( \ \sin \Delta \delta ≒\Delta \delta \ \)と近似するものとして,故障除去時の電気的トルクのステップ変化の大きさを\( \ \mathrm{p.u.} \ \)単位で求めよ。正弦関数の加法定理\( \ \sin (\alpha +\beta )=\sin\alpha \cos\beta +\cos\alpha \sin\beta \ \)を用いてよい。
(5) 高速再閉路の際に故障が継続していると再び電気的トルクが大きく変化する。タービン発電機には振動数\( \ \mathrm{10 \ Hz} \ \)程度の軸ねじれ現象が生じることを参考にして,高速再閉路のタイミングが\( \ 0.1 \ \)秒程度以下ずれるだけで軸の機械的疲労が大きく左右されることを説明せよ。
【ワンポイント解説】
一種の電力管理は二種と比べて計算問題の出題割合が少なく,出題されても本問のような難問が出題されるケースが多々あります。過去問でもあまり見たことがない問題であるため,試験日当日に解くためには,かなりの習熟が必要と考えられます。
1.系統の送電電力
送電電圧を\( \ V_{\mathrm {s}} \ \),受電電圧を\( \ V_{\mathrm {r}} \ \),送電線のリアクタンスを\( \ X \ \),\( \ V_{\mathrm {s}} \ \)と\( \ V_{\mathrm {r}} \ \)の相差角を\( \ \delta \ \)とすると,送電電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)短絡時の電気的トルクのステップ変化の大きさ
題意より電力とトルクは同じものと仮定し,タービン発電機は定格出力\( \ P_{\mathrm {n}}=1.0 \ [\mathrm {p.u.}] \ \),定格力率\( \ \cos \theta =0.9 \ \)で運転していたので,短絡前の電気的トルク\( \ P_{0} \ \)は,
\[
\begin{eqnarray}
P_{0} &=& P_{\mathrm {n}}\cos \theta \\[ 5pt ]
&=& 1.0\times 0.9 \\[ 5pt ]
&=& 0.9 \ [\mathrm {p.u.}]
\end{eqnarray}
\]
となる。一方,短絡発生後のトルク\( \ P_{1}≒0 \ \)となるから,短絡時の電気的トルクのステップ変化の大きさは,
\[
\begin{eqnarray}
P_{0}- P_{1}&=& 0.9-0 \\[ 5pt ]
&=& 0.9 \ [\mathrm {p.u.}]
\end{eqnarray}
\]
と求められる。
(2)故障発生後\( \ 0.1 \ \)秒間のタービン発電機の内部相差角増大量\( \ \Delta \delta \ \)
故障発生前の機械的入力は電気的出力と等しいので\( \ 0.9 \ \mathrm {p.u.} \ \)であり,故障発生後も変化しない。ゆえに,問題に与えられている微分方程式は,
\[
\begin{eqnarray}
M\frac {\mathrm {d}\omega }{\mathrm {d}t} &=& P_{\mathrm {m}}-P_{\mathrm {e}} \\[ 5pt ]
7\times \frac {\mathrm {d}\omega }{\mathrm {d}t} &=& 0.9 \ [\mathrm {p.u.}] \\[ 5pt ]
\frac {\mathrm {d}\omega }{\mathrm {d}t} &≒& 0.12857 \\[ 5pt ]
\mathrm {d}\omega &=& 0.12857 \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
と計算できる。事故発生前の\(\omega \)が0であることを考慮し,両辺を積分すると,
\[
\begin{eqnarray}
\omega&=&0.12857 t \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \Delta \delta =\int \omega \mathrm {d}t \ \)であるから,
\[
\begin{eqnarray}
\Delta \delta &=& \int ^{0.1}_{0} \omega \mathrm {d}t \\[ 5pt ]
&=& \int ^{0.1}_{0} 0.12857 t \mathrm {d}t \\[ 5pt ]
&=& \left[ 0.12857\cdot \frac {t^{2}}{2}\right] ^{0.1}_{0} \\[ 5pt ]
&=& 0.00064285 \ \mathrm {[p.u.]} \\[ 5pt ]
&=& 0.00064285 \times 2\pi f \ \mathrm {[rad]} \\[ 5pt ]
&=& 0.00064285 \times 2\pi \times 50 \ \mathrm {[rad]} \\[ 5pt ]
&≒& 0.20196\mathrm {[rad]} → 0.202 \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)故障発生前及び故障除去後(1回線運用中)の直列合成リアクタンス,\( \ x_{\mathrm {d}}^{\prime } \ \)背後電圧\( \ \dot E_{\mathrm {q}}^{\prime } \ \)の大きさと無限大母線電圧\( \ \dot V_{i} \ \)の大きさ
故障発生前の直列合成リアクタンス\( \ X_{0} \ \)は,タービン発電機のリアクタンス\( \ x_{\mathrm {d}}^{\prime }=0.3 \ \mathrm {p.u.} \ \)であるから,
\[
\begin{eqnarray}
X_{0}&=&0.3+0.1+\frac {0.1}{2}=0.45 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,故障除去後の直列合成リアクタンス\( \ X_{2} \ \)は,送電線が\( \ 1 \ \)回線となっていることから,
\[
\begin{eqnarray}
X_{2}&=&0.3+0.1+0.1=0.5 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。
発電機電流\( \ \dot I \ \mathrm {[p.u.]} \ \)とすると,
\[
\begin{eqnarray}
\dot I &=& 1.0 (\cos \theta +\mathrm {j}\sin \theta ) \\[ 5pt ]
&=& 1.0 (\cos \theta +\mathrm {j}\sqrt {1-\cos ^{2}\theta } ) \\[ 5pt ]
&=& 1.0 (0.9 +\mathrm {j}\sqrt {1-0.9^{2} } ) \\[ 5pt ]
&≒& 0.9+\mathrm {j}0.43589 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
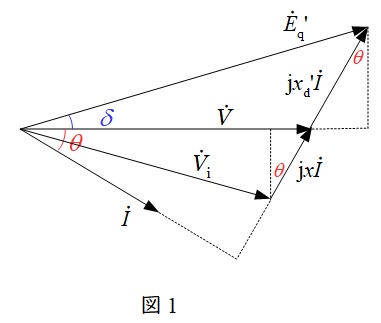
であり,発電機端子電圧を\( \ \dot V \ \)とすると電圧電流ベクトル図は図1のように描ける。よって,\( \ x_{\mathrm {d}}^{\prime } \ \)背後電圧\( \ \dot E_{\mathrm {q}}^{\prime } \ \)は,
\[
\begin{eqnarray}
\dot E_{\mathrm {q}}^{\prime } &=& \dot V+x_{\mathrm {d}}^{\prime }\dot I\sin \theta +\mathrm {j}x_{\mathrm {d}}^{\prime }\dot I\cos \theta \\[ 5pt ]
&=& 1.0+0.3\times 0.43589 +\mathrm {j} 0.3\times 0.9 \\[ 5pt ]
&≒& 1.1308+\mathrm {j}0.27 \ \mathrm {[p.u.]}
\end{eqnarray}
\]
と求められる。したがって,\( \ \dot E_{\mathrm {q}}^{\prime } \ \)の大きさは,
\[
\begin{eqnarray}
E_{\mathrm {q}}^{\prime } &=& \sqrt{1.1308^{2}+0.27^{2}} \\[ 5pt ]
&≒& 1.1626 \ \mathrm {[p.u.]} → 1.16 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
次に,無限大母線電圧\( \ \dot V_{\mathrm {i}} \ \)は,図1のベクトル図より,
\[
\begin{eqnarray}
\dot V_{\mathrm {i}} &=& \dot V-x\dot I\sin \theta -\mathrm {j}x\dot I\cos \theta \\[ 5pt ]
&=& 1.0-0.15\times 0.43589 -\mathrm {j}0.15\times 0.9 \\[ 5pt ]
&≒& 0.93462-\mathrm {j}0.135 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって,\( \ \dot V_{\mathrm {i}} \ \)の大きさは,
\[
\begin{eqnarray}
V_{\mathrm {i}} &=& \sqrt{0.93462^{2}+0.135^{2}} \\[ 5pt ]
&=& 0.94432 \mathrm {[p.u.]} → 0.944 \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)故障除去時の電気的トルクのステップ変化の大きさ
故障発生前の電気的トルク(=出力)\( \ P_{0} \ \)は,その時の相差角\( \ \delta \ \)とすると,ワンポイント解説「1.系統の送電電力」より,
\[
\begin{eqnarray}
P_{0}&=&\frac {E_{\mathrm {q}}^{\prime }V_{\mathrm {i}}}{X_{0}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
という関係があるので,各値を代入して\( \ \sin \delta \ \)を求めると,
\[
\begin{eqnarray}
0.9 &=& \frac {1.1626 \times 0.94432}{0.45}\sin \delta \\[ 5pt ]
\sin \delta &=& 0.36890 \\[ 5pt ]
\end{eqnarray}
\]
となる。また,\( \ \cos \delta \ \)は,
\[
\begin{eqnarray}
\cos \delta &=& \sqrt {1-\sin ^{2} \delta } \\[ 5pt ]
&=& \sqrt {1-0.36890^{2} } \\[ 5pt ]
&≒& 0.92950 \\[ 5pt ]
\end{eqnarray}
\]
故障除去後の電気的トルク(=出力)を\( \ P_{2} \ \)とすると,ワンポイント解説「1.系統の送電電力」より,
\[
\begin{eqnarray}
P_{2} &=& \frac {E_{\mathrm {q}}^{\prime }V_{\mathrm {i}}}{X_{2}}\sin (\delta +\Delta \delta ) \\[ 5pt ]
&=& \frac {E_{\mathrm {q}}^{\prime }V_{\mathrm {i}}}{X_{2}} (\sin \delta \cos \Delta \delta +\cos \delta \sin \Delta \delta )
\end{eqnarray}
\]
となり,\( \ \sin \Delta \delta ≒\Delta \delta \ \)とすると,
\[
\begin{eqnarray}
\cos \Delta \delta &=& \sqrt {1-\sin ^{2} \Delta \delta } \\[ 5pt ]
&=& \sqrt {1-\Delta \delta ^{2} } \\[ 5pt ]
&=& \sqrt {1- 0.20196 ^{2} } \\[ 5pt ]
&≒& 0.97939
\end{eqnarray}
\]
となるから,各値を代入すると\( \ P_{2} \ \)は,
\[
\begin{eqnarray}
P_{2} &=& \frac {E_{\mathrm {q}}^{\prime }V_{\mathrm {i}}}{X_{2}} (\sin \delta \cos \Delta \delta +\cos \delta \sin \Delta \delta ) \\[ 5pt ]
&≒& \frac {E_{\mathrm {q}}^{\prime }V_{\mathrm {i}}}{X_{2}} (\sin \delta \cos \Delta \delta +\cos \delta \cdot \Delta \delta ) \\[ 5pt ]
&=& \frac {1.1626 \times 0.94432}{0.5} \times (0.36890 \times 0.97939 +0.92950 \times 0.20196 ) \\[ 5pt ]
&≒& 1.2055 → 1.21 \ \mathrm {[p.u.]}
\end{eqnarray}
\]
と求められる。
(5)高速再閉路のタイミングが\( \ 0.1 \ \)秒程度以下ずれるだけで軸の機械的疲労が大きく左右されることの説明
(ポイント)
・再閉路時,事故除去されていない場合には,三相短絡が再度発生し,もう一度同様の軸ねじれ振動が発生する。
・たった\( \ 0.1 \ \)秒の間のことで大きな機械的応力が発生することを説明する。
(試験センター解答例)
再閉路時に故障点の短絡が解消されていない場合に,再閉路が行われると再び三相短絡が発生し,(1)で求めたような大きな電気的トルクが再び軸に加わることになる。このため軸は故障発生時に加速方向,故障除去時に減速方向,再閉路(失敗)時に再び加速方向の電気的トルクの急激な変化にさらされる。この大きな衝撃によって軸にはねじれ振動が発生するが,その減衰は一般に極めて悪く,固有振動数は\( \ 10 \ \mathrm {Hz} \ \)程度である。このため,再閉路失敗のタイミングが\( \ 0.1 \ \)秒程度以下の範囲で僅かに前後するだけで,その瞬間の軸のねじれ振動は様々な状態をとりうる。最悪の場合としては軸がちょうど加速しているところで再閉路失敗の加速方向のステップ変化を受けることも考えられ,この場合には軸は大きく機械的に歪むことになり,材料疲労は過酷となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん