【問題】
【難易度】★★★★☆(やや難しい)
次の表は,\( \ \mathrm {OF} \ \)ケーブルの異常診断法の測定内容と特徴(表1),及び絶縁破壊事故が発生した場合の事故点測定法の長所と短所,事故点までの距離(表2)に関する記述である。表中の\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \),\( \ \mathrm {D} \ \),\( \ \mathrm {E} \ \),\( \ \mathrm {F} \ \),\( \ \mathrm {G} \ \),\( \ \mathrm {H} \ \)及び\( \ \mathrm {I} \ \)の記号を付した空欄に記入すべき適切な語句又は式を答えなさい。
(表1)
\[
\begin{array}{|l|l|l|}
\hline
異常診断法 & 測 定 内 容 & 特 徴 \\
\hline
油中ガス & 採取した絶縁油中に溶解した & 分析結果のガスの \ \fbox {$\hskip 1em $ $\mathrm {A}$ $\hskip 1em $} \ \\
分析 & 放電や熱分解などによる & や \ \fbox {$\hskip 1em $ $\mathrm {B}$ $\hskip 1em $} \ により,異常の有 \\
& 分解生成ガスを抽出・分析 & 無と異常の程度を推定すること \\
& する。 & が可能である。 \\
\hline
絶縁油特性 & 採取した絶縁油の各特性 & 各特性の測定結果により, \\
測定 & ( \ \fbox {$\hskip 1em $ $\mathrm {C}$ $\hskip 1em $} \ , \ \fbox {$\hskip 1em $ $\mathrm {D}$ $\hskip 1em $} \ , & 施工不良,気密性,絶縁油の \\
& \ \fbox {$\hskip 1em $ $\mathrm {E}$ $\hskip 1em $} \ ,全酸価,絶縁 & 汚損状況,熱劣化等を推定する \\
& 破壊電圧)を測定する。 & ことで,異常の程度を推定する \\
& & ことが可能である。 \\
\hline
コアずれ & 放射線によりケーブルや & セミストップ部の変形,遮へい \\
測定 & 接続箱の内部を撮影し, & 層の乱れや,コアずれ量による \\
& 内部状況を調査する。 & 接続箱内の \ \fbox {$\hskip 1em $ $\mathrm {F}$ $\hskip 1em $} \ \\
& & を把握し,油中ガス分析と組み \\
& & 合わせることで,異常の程度を \\
& & 推定することが可能である。 \\
\hline
部分放電 & 発生している部分放電を & 油中ガス分析では検出困難な \\
測定 & 測定し,一定時間内に発生 & \ \fbox {$\hskip 1em $ $\mathrm {G}$ $\hskip 1em $} \ に有効である。 \\
& する部分放電パルス数等を & 停電ができない電線路の測定が \\
& 電圧や時間で整理する。 & 可能である。 \\
\hline
\end{array}
\]
(表2)
\[
\begin{array}{|l|l|l|l|}
\hline
{\displaystyle 事故点}\atop {\displaystyle 測定法} & 長 所 & 短 所 &{\displaystyle 測定端から }\atop {\displaystyle 事故点までの距離:l} \\
\hline
マーレー & 導体抵抗を利用 & 並行健全相がない & ケーブル全長をL / 相, \\
ループ法 & したホイートス & 場合,事故点が & 測定辺抵抗をR_{1},R_{2} \\
& トンブリッジ法の & 放電する場合, & とすると, \\
& ため,測定精度が & \ \fbox {$\hskip 1em $ $\mathrm {H}$ $\hskip 1em $} \ & l \ は \ \fbox {$\hskip 1em $ $\mathrm {I}$ $\hskip 1em $} \ \\
& 高く,誤差は & には適用すること & と表される。 \\
& 1 \ \mathrm {[%]} \ 程度以下 & ができない。 & \\
& である。 & & \\
\hline
パルス & パルス電圧を & 測定操作,パルス & 第 \ 1 \ 波パルスと第 \ 2 \ 波パ \\
レーダ法 & 送出し,事故点 & 波形の判読に熟練 & ルスの時間差を \ t \ ,ケー \\
& からの反射パルス & を要する。 & ブル内のサージ伝搬速度 \\
& を検知するため, & & を \ v \ とすると, \ l \ は \ \displaystyle \frac {v\cdot t}{2} \ \\
& 地絡,短絡事故や & & と表される。 \\
& \ \fbox {$\hskip 1em $ $\mathrm {H}$ $\hskip 1em $} \ & & \\
& に適用できる。 & & \\
\hline
\end{array}
\]
【ワンポイント解説】
文中穴埋め問題が出題されることがありますが,部分点が一切認められないため,個人的にはあまりおすすめできません。時間がない場合に選択するのはOKだと思います。
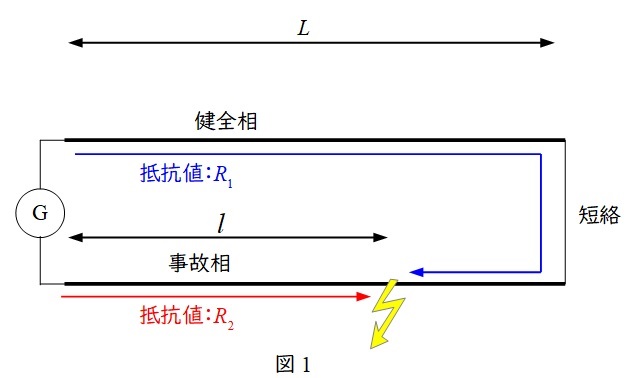
1.マーレーループ法
ホイーストンブリッジの原理を利用して,地絡事故点までの距離を測定する方法です。図1のように健全相と事故相があり,健全相側の抵抗を\( \ R_{1} \ \),事故相側の抵抗を\( \ R_{2} \ \)とすると,事故点までの距離\( \ l \ \)は,
\[
\begin{eqnarray}
\frac {R_{1}}{2L-l}&=&\frac {R_{2}}{l} \\[ 5pt ]
R_{1}l&=&R_{2}\left( 2L-l\right) \\[ 5pt ]
l&=&\frac {2R_{2}}{R_{1}+R_{2}}L \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
2.パルスレーダ法
パルス法は問題図に描かれている方法で事故点での反射パルスを検知して,事故点までの距離を求める方法です。パルスの伝搬速度を\( \ v \ \)とすると,測定点と事故点までの距離\( \ x \ \)は,
\[
\begin{eqnarray}
x&=&\frac {vt}{2} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(A)量,(B)種類(順不同)
(C)水分量,(D)体積抵抗率,(E)誘電正接(順不同)
(F)絶縁紙のずれや損傷
(G)ケーブル部の部分放電発生位置の測定
(H)断線事故
(I)\(\displaystyle \frac {2LR_{2}}{R_{1}+R_{2}}\)もしくは\(\displaystyle \frac {2LR_{1}}{R_{1}+R_{2}}\)






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん