《電力・管理》〈変電〉[H27:問3] 変圧器タップ動作による電圧不安定現象に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

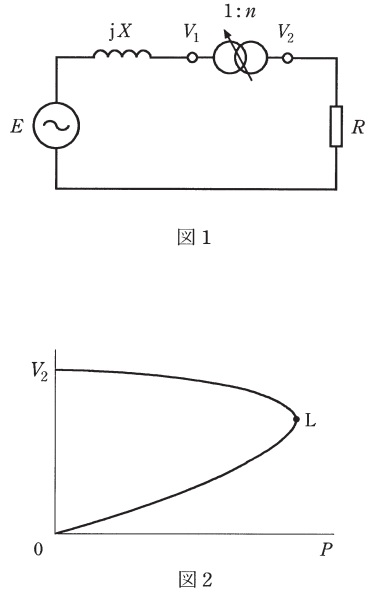
図1及び図2は，電力系統の変圧器タップ動作による電圧不安定現象に関する原理的な説明図である。$E$と$\mathrm {j}X$はそれぞれ注目している地点の背後電圧値と短絡インピーダンスであり，負荷は力率$100％$の静的要素であると考え，等価抵抗$R$で表現している。また，図中に示す変圧器の巻数比($1：n$)は負荷時電圧調整器によって二次側電圧値$V_{2}$が低くなると$n$を上げるように自動制御されていると仮定し，その漏れリアクタンスや励磁アドミタンスは無視できるものとする。$V_{1}$は変圧器の一次側電圧値である。次の問に答えよ。

(1)　$V_{2}$を$R$，$X$，$n$，$E$を用いて書き表すと，
$$V_{2}=\frac {R}{\sqrt {\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}}}E$$ となる。空欄に入るべき式を答えよ。

(2)　上記(1)にて求めた式において，$n$以外のパラメータは全て一定であるとして，$n$が変化したときに$V_{2}$がどのように変化するか考える。通常$n$を増やすと$V_{2}$は上昇するが，低下する場合が考えられる。それはどのような場合か，$R$，$n$及び$X$の間で成立する不等式の形で答えよ。

(3)　上記(2)にて求めた条件で，変圧器タップ動作による不安定現象が発生することを説明せよ。

(4)　$R$以外のパラメータを全て一定に保ったまま$R$のみを変化させて，$R$の消費する電力$P$(横軸)と$V_{2}$(縦軸)との間の関係を図示すると図2のような形状となり，$P-V$カーブあるいはノーズカーブと呼ばれる。その先端$\mathrm {L}$が上記(2)で検討した安定性の限界点に対応することを説明せよ。

【ワンポイント解説】

一種としては，比較的取り組みやすい計算問題と言えます。落ち着いて回路計算と微分の計算を行うようにしましょう。

1.変圧器の一次側換算
変圧器の一次側の巻数が$N_{1}$，$N_{2}$である時，二次側電圧$V_{2}$，二次側電流$I_{2}$，二次側インピーダンス$Z_{2}$の一次側換算は，
$$\begin{eqnarray} {V_{2}}^{\prime } &=& \frac {N_{1}}{N_{2}}V_{2} \\[ 5pt ] {I_{2}}^{\prime } &=& \frac {N_{2}}{N_{1}}I_{2} \\[ 5pt ] {Z_{2}}^{\prime } &=& \left( \frac {N_{1}}{N_{2}}\right) ^{2}Z_{2} \\[ 5pt ] \end{eqnarray}$$ となります。

【関連する「電気の神髄」記事】

　　電力系統のP-V曲線と電圧安定性
　　変圧器タップの逆動作現象（電圧不安定現象）

【解答】

(1)$V_{2}$を$R$，$X$，$n$，$E$を用いて書き表す
$V_{2}$及び$R$を一次側に換算すると，$\displaystyle \frac {V_{2}}{n}$，$\displaystyle \frac {R}{n^{2}}$となるので，
$$\begin{eqnarray} \frac {{\dot V}_{2}}{n} &=& \frac {\displaystyle \frac {R}{n^{2}}}{\displaystyle \frac {R}{n^{2}}+\mathrm {j}X}\dot E \\[ 5pt ] {\dot V}_{2} &=& \frac {\displaystyle \frac {R}{n}}{\displaystyle \frac {R}{n^{2}}+\mathrm {j}X}\dot E \\[ 5pt ] &=& \frac { R}{\displaystyle \frac {R}{n}+\mathrm {j}nX}\dot E \\[ 5pt ] \end{eqnarray}$$ となる。よって，その大きさは，
$$\begin{eqnarray} V_{2} &=& \frac {R}{\sqrt {\displaystyle \frac {R^{2}}{n^{2}}+n^{2}X^{2}}}E \\[ 5pt ] \end{eqnarray}$$ と求められる。

(2)$n$を増やすと$V_{2}$が低下する時に成立する不等式
$\displaystyle A=\frac {R^{2}}{n^{2}}+n^{2}X^{2}$とすると，
$$\begin{eqnarray} \frac {\mathrm {d}V_{2}}{\mathrm {d}n} &=& \frac {\mathrm {d}V_{2}}{\mathrm {d}A}\cdot \frac {\mathrm {d}A}{\mathrm {d}n} \\[ 5pt ] &=& RE\left( -\frac {1}{2}A^{-\frac {3}{2}}\right) \cdot \left( -2\frac {R^{2}}{n^{3}}+2nX^{2}\right) \\[ 5pt ] &=& RE\left( \frac {R^{2}}{n^{2}}+n^{2}X^{2}\right) ^{-\frac {3}{2}}\cdot \left( \frac {R^{2}}{n^{3}}-nX^{2}\right) \\[ 5pt ] \end{eqnarray}$$ となる。$n$を増やすと$V_{2}$が低下するのは$\displaystyle \frac {\mathrm {d}V_{2}}{\mathrm {d}n} ＜ 0$の時であるから，$n＞0$であることに注意すると，
$$\begin{eqnarray} RE\left( \frac {R^{2}}{n^{2}}+n^{2}X^{2}\right) ^{-\frac {3}{2}}\cdot \left( \frac {R^{2}}{n^{3}}-nX^{2}\right) &＜& 0 \\[ 5pt ] \frac {R^{2}}{n^{3}}-nX^{2}&＜& 0 \\[ 5pt ] n^{4}&＞& \frac {R^{2}}{X^{2}} \\[ 5pt ] n&＞& \sqrt {\frac {R}{X}} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(3)(2)にて求めた条件で，変圧器タップ動作による不安定動作が発生することを説明
題意の通り変圧器タップ動作では二次側電圧$V_{2}$が低くなると$n$を上げるよう自動制御されているが，上記(2)にて求めた条件下で$V_{2}$が低下すると$n$が増大し，これが更なる$V_{2}$の低下を生む。よって，電圧が不安定動作が発生する。

(4)ノーズカーブの先端$\mathrm {L}$が上記(2)で検討した安定性の限界点に対応することを説明
$R$で消費する電力$P$は，
$$\begin{eqnarray} P &=& \frac {V_{2}^{2}}{R} \\[ 5pt ] &=& \frac {\left( \frac {\displaystyle R}{\sqrt {\displaystyle \frac {R^{2}}{n^{2}}+n^{2}X^{2}}}E\right) ^{2}}{R} \\[ 5pt ] &=& \frac {\displaystyle RE^{2}}{\displaystyle \frac {R^{2}}{n^{2}}+n^{2}X^{2}} \\[ 5pt ] &=& \frac {\displaystyle E^{2}}{\displaystyle \frac {R}{n^{2}}+\frac {n^{2}X^{2}}{R}} \\[ 5pt ] \end{eqnarray}$$ となる。よって，最大電力$P$を取るとき，$P$の分母が最小となれば良いから，$\displaystyle A=\frac {R}{n^{2}}+\frac {n^{2}X^{2}}{R}$と置くと，
$$\begin{eqnarray} \frac {\mathrm {d}A}{\mathrm {d}R} &=& \frac {1}{n^{2}}-\frac {n^{2}X^{2}}{R^{2}}=0 \\[ 5pt ] \frac {1}{n^{2}}&=& \frac {n^{2}X^{2}}{R^{2}} \\[ 5pt ] n&=& \sqrt {\frac {R}{X}} \\[ 5pt ] \end{eqnarray}$$ となり，(2)の安定性の限界点と一致している。