《電力・管理》〈送電〉[R02:問4]三相地絡事故発生時の地絡距離リレーの動作に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

図に示すような架空送電系統において，母線\( \ 2 \ \)から区間\( \ \mathrm {B} \ \)の\( \ 40 \ ％ \ \)の距離にあたる点\( \ \mathrm {F} \ \)で三相地絡事故が発生した。区間\( \ \mathrm {B} \ \)での主保護リレーが誤不動作し，母線\( \ 2 \ \)と母線\( \ 3 \ \)側の線路遮断器が閉じたままで事故が継続中である。このとき区間\( \ \mathrm {A} \ \)の母線\( \ 1 \ \)側に設置された後備保護リレーである地絡距離リレー\( \ \mathrm {RyA} \ \)の動作に関して，次の問に答えよ。

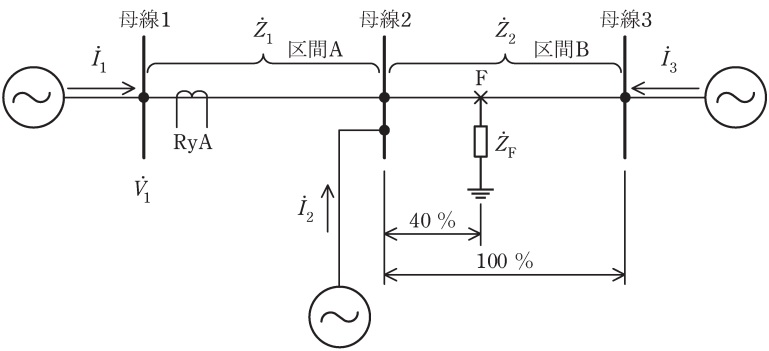
ただし，図に示した\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)，\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{2} \ \mathrm {[A]} \ \)，\( \ {\dot I}_{3} \ \mathrm {[A]} \ \)，\( \ {\dot Z}_{1} \ \mathrm {[\Omega ]} \ \)，\( \ {\dot Z}_{2} \ \mathrm {[\Omega ]} \ \)，\( \ {\dot Z}_{\mathrm {F}} \ \mathrm {[\Omega ]} \ \)は，計器用変成器二次側に換算した相電圧値，相電流値，インピーダンス値である。\( \ \mathrm {RyA} \ \)が測定する距離インピーダンスの大きさは\( \ \left| \displaystyle \frac {{\dot V}_{1}}{{\dot I}_{1}} \right| \ \)で演算される。\( \ {\dot Z}_{1} \ \)，\( \ {\dot Z}_{2} \ \)はそれぞれ区間\( \ \mathrm {A} \ \)，区間\( \ \mathrm {B} \ \)の送電線インピーダンス，\( \ {\dot Z}_{\mathrm {F}} \ \)は\( \ \mathrm {F} \ \)点での故障点インピーダンスで，全て\( \ 1 \ \)相あたりとする。負荷電流と充電電流は無視できるものとする。

(2)　\( \ \mathrm {RyA} \ \)の整定値が\( \ {\dot Z}_{1} \ \)の大きさに対するパーセント値で表される場合，\( \ \mathrm {RyA} \ \)が動作域にあるためには，整定値は何パーセント以上であればよいか。\( \ \displaystyle \frac {{\dot I}_{2}}{{\dot I}_{1}} \ \)，\( \ \displaystyle \frac {{\dot I}_{3}}{{\dot I}_{1}} \ \)を計算し，整定値は最小値で求めよ。
ただし，\( \ \mathrm {RyA} \ \)が測定する距離インピーダンスの大きさが整定値以下になると\( \ \mathrm {RyA} \ \)は動作域にあるものとし，\( \ {\dot I}_{1} \ \)，\( \ {\dot I}_{2} \ \)，\( \ {\dot I}_{3} \ \)，\( \ {\dot Z}_{1} \ \)，\( \ {\dot Z}_{2} \ \)，\( \ {\dot Z}_{\mathrm {F}} \ \)は次の値とする。
\[
\begin{eqnarray}
&&{\dot I}_{1}=30+\mathrm {j}0.0 \ \mathrm {A}，{\dot I}_{2}=21-\mathrm {j}3.6 \ \mathrm {A}，{\dot I}_{3}=15-\mathrm {j}3.9 \ \mathrm {A}， \\[ 5pt ] &&{\dot Z}_{1}=0.35+\mathrm {j}2.0 \ \mathrm {\Omega }，{\dot Z}_{2}=0.22+\mathrm {j}1.2 \ \mathrm {\Omega }，{\dot Z}_{\mathrm {F}}=0.10+\mathrm {j}0.0 \ \mathrm {\Omega } \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

リレーの整定値に関する問題ですが，内容はリレーではなくほとんど回路計算のような内容となっています。
電験\( \ 1 \ \)種の二次試験は難易度が高い問題も多いですが，本問のように比較的取り組みやすい問題も出題され，このような問題を計算間違いせず解けるかどうかが合否の分けることになります。

【解答】

(1)\( \ \mathrm {RyA} \ \)が測定する\( \ {\dot V}_{1} \ \)を\( \ {\dot I}_{1} \ \)，\( \ {\dot I}_{2} \ \)，\( \ {\dot I}_{3} \ \)，\( \ {\dot Z}_{1} \ \)，\( \ {\dot Z}_{2} \ \)，\( \ {\dot Z}_{\mathrm {F}} \ \)を用いて表す
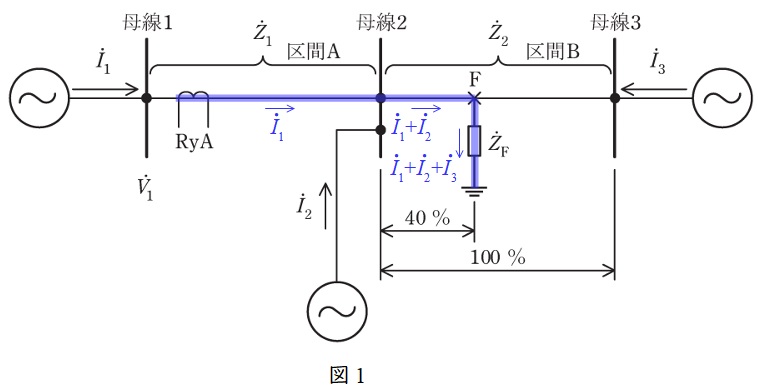
\( \ \mathrm {RyA} \ \)が測定する電圧\( \ {\dot V}_{1} \ \)は，図1に示す区間の電圧降下を求めれば良い。
それぞれの区間を流れる電流は図1の通りであるから，区間\( \ \mathrm {A} \ \)での電圧降下\( \ {\dot V}_{\mathrm {A}} \ \)，母線\( \ 2 \ \)から点\( \ \mathrm {F} \ \)までの電圧降下\( \ {\dot V}_{\mathrm {B}} \ \)，\( \ {\dot Z}_{\mathrm {F}} \ \)での電圧降下\( \ {\dot V}_{\mathrm {F}} \ \)は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {A}}&=&{\dot Z}_{1}{\dot I}_{1} \\[ 5pt ] {\dot V}_{\mathrm {B}}&=&0.4{\dot Z}_{2}\left( {\dot I}_{1}+{\dot I}_{2}\right) \\[ 5pt ] {\dot V}_{\mathrm {F}}&=&{\dot Z}_{\mathrm {F}}\left( {\dot I}_{1}+{\dot I}_{2}+{\dot I}_{3}\right) \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ \mathrm {RyA} \ \)が測定する\( \ {\dot V}_{1} \ \)は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {1}}&=&{\dot V}_{\mathrm {A}}+{\dot V}_{\mathrm {B}}+{\dot V}_{\mathrm {F}} \\[ 5pt ] &=&{\dot Z}_{1}{\dot I}_{1}+0.4{\dot Z}_{2}\left( {\dot I}_{1}+{\dot I}_{2}\right) +{\dot Z}_{\mathrm {F}}\left( {\dot I}_{1}+{\dot I}_{2}+{\dot I}_{3}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)\( \ \mathrm {RyA} \ \)が動作域にあるためには，整定値は\( \ {\dot Z}_{1} \ \)の何パーセント以上か
題意より，\( \ \mathrm {RyA} \ \)が測定する距離インピーダンスの大きさは\( \ \left| \displaystyle \frac {{\dot V}_{1}}{{\dot I}_{1}} \right| \ \)で求められるので，
\[
\begin{eqnarray}
\left| \displaystyle \frac {{\dot V}_{1}}{{\dot I}_{1}} \right| &=&\left| \displaystyle \frac {{\dot Z}_{1}{\dot I}_{1}+0.4{\dot Z}_{2}\left( {\dot I}_{1}+{\dot I}_{2}\right) +{\dot Z}_{\mathrm {F}}\left( {\dot I}_{1}+{\dot I}_{2}+{\dot I}_{3}\right)}{{\dot I}_{1}} \right| \\[ 5pt ] &=&\left| {\dot Z}_{1} +0.4{\dot Z}_{2}\left( 1+\frac {{\dot I}_{2}}{{\dot I}_{1}}\right) + {\dot Z}_{\mathrm {F}}\left( 1+\frac {{\dot I}_{2}}{{\dot I}_{1}}+\frac {{\dot I}_{3}}{{\dot I}_{1}}\right)\right| 　・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。ここで，
\[
\begin{eqnarray}
\frac {{\dot I}_{2}}{{\dot I}_{1}} &=&\frac {21-\mathrm {j}3.6}{30+\mathrm {j}0.0} \\[ 5pt ] &=&0.7-\mathrm {j}0.12 \\[ 5pt ] \frac {{\dot I}_{3}}{{\dot I}_{1}} &=&\frac {15-\mathrm {j}3.9}{30+\mathrm {j}0.0} \\[ 5pt ] &=&0.5-\mathrm {j}0.13 \\[ 5pt ] \end{eqnarray}
\] であるから，①式に各値を代入すると，
\[
\begin{eqnarray}
\left| \displaystyle \frac {{\dot V}_{1}}{{\dot I}_{1}} \right| &=&\left| 0.35+\mathrm {j}2.0 +0.4\times \left( 0.22+\mathrm {j}1.2\right) \times \left( 1+0.7-\mathrm {j}0.12\right) + \left( 0.10+\mathrm {j}0.0\right) \times \left( 1+0.7-\mathrm {j}0.12+0.5-\mathrm {j}0.13\right)\right| \\[ 5pt ] &=&\left| 0.35+\mathrm {j}2.0 + \left( 0.088+\mathrm {j}0.48\right) \times \left( 1.7-\mathrm {j}0.12\right) + 0.10 \times \left( 2.2-\mathrm {j}0.25\right)\right| \\[ 5pt ] &=&\left| 0.35+\mathrm {j}2.0 + 0.1496-\mathrm {j}0.01056+\mathrm {j}0.816+0.0576+ 0.22-\mathrm {j}0.025\right| \\[ 5pt ] &=&\left| 0.7772+\mathrm {j}2.78044\right| \\[ 5pt ] &=&\sqrt {0.7772^{2}+2.78044^{2}} \\[ 5pt ] &≒&2.8870 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，\( \ \left| {\dot Z}_{1}\right| \ \)は，
\[
\begin{eqnarray}
\left| {\dot Z}_{1}\right| &=&\left| 0.35+\mathrm {j}2.0 \right| \\[ 5pt ] &=&\sqrt {0.35^{2}+2.0^{2}} \\[ 5pt ] &≒&2.0304 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] であるので，\( \ \mathrm {RyA} \ \)の整定値は，
\[
\begin{eqnarray}
\frac {\left| \displaystyle \frac {{\dot V}_{1}}{{\dot I}_{1}} \right| }{\left| {\dot Z}_{1}\right| }\times 100 &=&\frac {2.8870}{2.0304}\times 100 \\[ 5pt ] &≒&142.19 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] よりも大きい値となる。すなわち\( \ \mathrm {RyA} \ \)の動作域は\( \ 143 \ \mathrm {％} \ \)以上であればよい。