【問題】
【難易度】★☆☆☆☆(易しい)
簡易法による潮流計算に関して,次の問に答えよ。
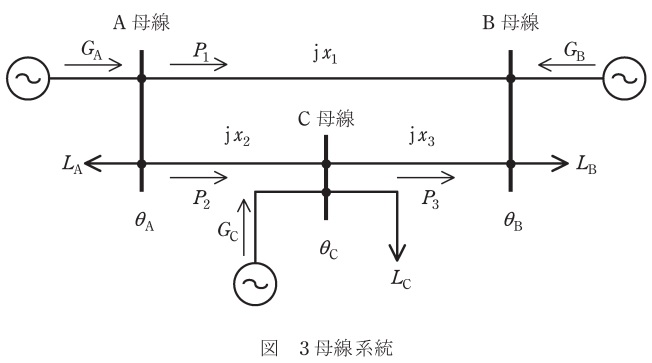
図において,\( \ \mathrm {A} \ \)母線の電圧位相を\( \ \theta _{\mathrm {A}} \ \),\( \ \mathrm {A} \ \)母線に接続される発電出力を\( \ G_{\mathrm {A}} \ \),負荷を\( \ L_{\mathrm {A}} \ \)とする。ここで,\( \ \mathrm {A} \ \)母線への正味注入電力を\( \ P_{\mathrm {A}}=G_{\mathrm {A}}-L_{\mathrm {A}} \ \)とし,\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \)母線でも同様の表記とする。また,各送電線の潮流\( \ P_{1} \ \),\( \ P_{2} \ \),\( \ P_{3} \ \)は図の向きを正とし,送電線では図の\( \ x_{1} \ \),\( \ x_{2} \ \),\( \ x_{3} \ \)のリアクタンスのみを考慮する。発電出力,負荷,潮流は有効電力のみを考慮し,数値はリアクタンスも含め単位法での値とする。ただし,位相の単位は\( \ \mathrm {[rad]} \ \)である。
各母線の電圧は\( \ 1 \ \),電圧の位相差は小さいとする。この場合,送電線を流れる有効電力の近似式は,例えば\( \ P_{1} \ \)は①式で表される。これを簡易法による潮流計算と称する。
\[
\begin{eqnarray}
P_{1}&=&\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {B}}}{x_{1}} ・・・・・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
以下の小問(1),及び,簡易法による潮流計算を用いて小問(2)~(4)に答えよ。
(1)\( \ x_{1}=0.1 \ \),\( \ \displaystyle \theta _{\mathrm {A}}-\theta _{\mathrm {B}}=\frac {\pi }{12} \ \),各母線の電圧は\( \ 1 \ \)とする。①式による\( \ P_{1} \ \)の近似値と,①式の近似を用いない場合の\( \ P_{1} \ \)の真値を求めよ。ただし,\( \ \pi =3.1416 \ \)を用い,\( \ \displaystyle \sin ^{2}\theta =\frac {1-\cos 2 \theta }{2} \ \)の関係式を用いてよい。
(2)\( \ \theta _{\mathrm {B}} \ \)を基準(\( \ \theta _{\mathrm {B}}=0 \ \))とし,\( \ P_{\mathrm {A}} \ \)と\( \ P_{\mathrm {C}} \ \)を,\( \ \theta _{\mathrm {A}} \ \),\( \ \theta _{\mathrm {C}} \ \)及び\( \ x_{1} \ \),\( \ x_{2} \ \),\( \ x_{3} \ \)で表せ。
(3)\( \ x_{1}=0.05 \ \),\( \ x_{2}=0.02 \ \),\( \ x_{3}=0.03 \ \)の場合の,\( \ \theta _{\mathrm {A}} \ \),\( \ \theta _{\mathrm {C}} \ \)及び\( \ P_{1} \ \),\( \ P_{2} \ \),\( \ P_{3} \ \)を求めよ。ただし,\( \ \theta _{\mathrm {B}} \ \)を基準(\( \ \theta _{\mathrm {B}}=0 \ \))とする。また,\( \ G_{\mathrm {A}}=20 \ \),\( \ G_{\mathrm {B}}=30 \ \),\( \ G_{\mathrm {C}}=14 \ \),\( \ L_{\mathrm {A}}=10 \ \),\( \ L_{\mathrm {B}}=46 \ \),\( \ L_{\mathrm {C}}=8 \ \)である。
(4)\( \ P_{1}=6 \ \)とするように,発電出力\( \ G_{\mathrm {A}} \ \)と\( \ G_{\mathrm {B}} \ \)を調整する。\( \ G_{\mathrm {A}} \ \)と\( \ G_{\mathrm {B}} \ \)を求めよ。ただし,\( \ G_{\mathrm {A}} \ \)と\( \ G_{\mathrm {B}} \ \)以外の条件は小問(3)と同じとする。
【ワンポイント解説】
電験一種の二次試験としては,易しいレベルの問題になると思います。毎年一種でも一問程度は易しい計算問題が設定されている印象があります。一種の一次試験合格者であれば解ける問題ではあると思います。あとはいかに速く正確に解けるかが合否の分かれ目になりますので,できるだけ速く解けるように学習を進めて下さい。
1.送電電力\( \ P \ \)
送電端の電圧が\( \ V_{\mathrm {s}} \ \),受電端の電圧が\( \ V_{\mathrm {r}} \ \)であり,その位相差が\( \ \theta \ \),送電線のリアクタンスが\( \ x \ \)の時の送電電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{x}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)①式による\( \ P_{1} \ \)の近似値と,①式の近似を用いない場合の\( \ P_{1} \ \)の真値
【近似値】
①式に各値を代入すると,
\[
\begin{eqnarray}
P_{1}&=&\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {B}}}{x_{1}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {\pi }{12}}{0.1} \\[ 5pt ]
&=&2.618 → 2.62 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
【真値】
ワンポイント解説「1.送電電力\( \ P \ \)」より,
\[
\begin{eqnarray}
P_{1}&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{x_{1}}\sin \left( \theta _{\mathrm {A}}-\theta _{\mathrm {B}}\right) \\[ 5pt ]
&=&\frac {1\times 1}{0.1}\sin \frac {\pi }{12} \\[ 5pt ]
&=&10\sqrt {\frac {1-\cos \frac {\pi }{6}}{2}} \\[ 5pt ]
&=&10\sqrt {\frac {1-\frac {\sqrt {3}}{2}}{2}} \\[ 5pt ]
&≒&2.5882 → 2.59 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ \theta _{\mathrm {B}} \ \)を基準(\( \ \theta _{\mathrm {B}}=0 \ \))とし,\( \ P_{\mathrm {A}} \ \)と\( \ P_{\mathrm {C}} \ \)を,\( \ \theta _{\mathrm {A}} \ \),\( \ \theta _{\mathrm {C}} \ \)及び\( \ x_{1} \ \),\( \ x_{2} \ \),\( \ x_{3} \ \)で表す
各送電線を流れる有効電力を求める式は,①式を用いると,
\[
\begin{eqnarray}
P_{1}&=&\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {B}}}{x_{1}} \\[ 5pt ]
&=&\frac {\theta _{\mathrm {A}}}{x_{1}} &・・・・・・・・・・・・・・ ②& \\[ 5pt ]
P_{2}&=&\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {C}}}{x_{2}} &・・・・・・・・・・・・・・ ③& \\[ 5pt ]
P_{3}&=&\frac {\theta _{\mathrm {C}}-\theta _{\mathrm {B}}}{x_{3}} \\[ 5pt ]
&=&\frac {\theta _{\mathrm {C}}}{x_{3}} &・・・・・・・・・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
となる。各母線に流入する電力と流出する電力は等しいので,\( \ \mathrm {A} \ \)母線においては,
\[
\begin{eqnarray}
G_{\mathrm {A}}&=&P_{1}+P_{2}+L_{\mathrm {A}} \\[ 5pt ]
\end{eqnarray}
\]
が成立し,\( \ P_{\mathrm {A}}=G_{\mathrm {A}}-L_{\mathrm {A}} \ \)であることに注意して整理すると,
\[
\begin{eqnarray}
G_{\mathrm {A}}-L_{\mathrm {A}}&=&P_{1}+P_{2} \\[ 5pt ]
P_{\mathrm {A}}&=&\frac {\theta _{\mathrm {A}}}{x_{1}}+\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {C}}}{x_{2}} ・・・・・・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
と求められる。同様に,\( \ \mathrm {C} \ \)母線においては,
\[
\begin{eqnarray}
G_{\mathrm {C}}+P_{2}&=&P_{3}+L_{\mathrm {C}} \\[ 5pt ]
\end{eqnarray}
\]
が成立し,\( \ P_{\mathrm {C}}=G_{\mathrm {C}}-L_{\mathrm {C}} \ \)であることに注意して整理すると,
\[
\begin{eqnarray}
G_{\mathrm {C}}-L_{\mathrm {C}}&=&-P_{2}+P_{3} \\[ 5pt ]
P_{\mathrm {C}}&=&-\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {C}}}{x_{2}}+\frac {\theta _{\mathrm {C}}}{x_{3}} ・・・・・・・・・・・・・・ ⑥ \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ x_{1}=0.05 \ \),\( \ x_{2}=0.02 \ \),\( \ x_{3}=0.03 \ \)の場合の,\( \ \theta _{\mathrm {A}} \ \),\( \ \theta _{\mathrm {C}} \ \)及び\( \ P_{1} \ \),\( \ P_{2} \ \),\( \ P_{3} \ \)
(2)の⑤,⑥式に各値を代入して整理すると,
\[
\begin{eqnarray}
P_{\mathrm {A}}&=&\frac {\theta _{\mathrm {A}}}{x_{1}}+\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {C}}}{x_{2}} \\[ 5pt ]
20-10&=&\frac {\theta _{\mathrm {A}}}{0.05}+\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {C}}}{0.02} \\[ 5pt ]
10&=&20\theta _{\mathrm {A}}+50\left( \theta _{\mathrm {A}}-\theta _{\mathrm {C}}\right) \\[ 5pt ]
10&=&70\theta _{\mathrm {A}}-50\theta _{\mathrm {C}} \\[ 5pt ]
1&=&7\theta _{\mathrm {A}}-5\theta _{\mathrm {C}} &・・・・・・・・・・・・・・ ⑦& \\[ 5pt ]
P_{\mathrm {C}}&=&-\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {C}}}{x_{2}}+\frac {\theta _{\mathrm {C}}}{x_{3}} \\[ 5pt ]
14-8&=&-\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {C}}}{0.02}+\frac {\theta _{\mathrm {C}}}{0.03} \\[ 5pt ]
6&=&-\frac {3\left( \theta _{\mathrm {A}}-\theta _{\mathrm {C}}\right) }{0.06}+\frac {2\theta _{\mathrm {C}}}{0.06} \\[ 5pt ]
6\times 0.06&=&-3\left( \theta _{\mathrm {A}}-\theta _{\mathrm {C}}\right) +2\theta _{\mathrm {C}} \\[ 5pt ]
0.36&=&-3\theta _{\mathrm {A}}+5\theta _{\mathrm {C}} &・・・・・・・・・・・・・・ ⑧& \\[ 5pt ]
\end{eqnarray}
\]
となる。⑦,⑧を解くと,
\[
\begin{eqnarray}
\theta _{\mathrm {A}}&=&0.34 \ \mathrm {[rad]} \\[ 5pt ]
\theta _{\mathrm {C}}&=&0.276 \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,これを②,③,④に代入すると,
\[
\begin{eqnarray}
P_{1}&=&\frac {\theta _{\mathrm {A}}}{x_{1}} \\[ 5pt ]
&=&\frac {0.34}{0.05} \\[ 5pt ]
&=&6.8 \ \mathrm {[p.u.]} \\[ 5pt ]
P_{2}&=&\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {C}}}{x_{2}} \\[ 5pt ]
&=&\frac {0.34-0.276}{0.02} \\[ 5pt ]
&=&3.2 \ \mathrm {[p.u.]} \\[ 5pt ]
P_{3}&=&\frac {\theta _{\mathrm {C}}}{x_{3}} \\[ 5pt ]
&=&\frac {0.276}{0.03} \\[ 5pt ]
&=&9.2 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ P_{1}=6 \ \)とするような\( \ G_{\mathrm {A}} \ \)と\( \ G_{\mathrm {B}} \ \)の値
\( \ G_{\mathrm {A}} \ \)と\( \ G_{\mathrm {B}} \ \)以外の条件は(3)と同じなので,①~⑧式のうち,⑦以外の関係式はすべて成立する。
②より,
\[
\begin{eqnarray}
P_{1}&=&\frac {\theta _{\mathrm {A}}}{x_{1}} \\[ 5pt ]
6&=&\frac {\theta _{\mathrm {A}}}{0.05} \\[ 5pt ]
\theta _{\mathrm {A}}&=&0.3 \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
となる。これを⑧式に代入すると,
\[
\begin{eqnarray}
0.36&=&-3\theta _{\mathrm {A}}+5\theta _{\mathrm {C}} \\[ 5pt ]
0.36&=&-3\times 0.3+5\theta _{\mathrm {C}} \\[ 5pt ]
\theta _{\mathrm {C}}&=&0.252 \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
となる。③,④式に各値を代入すると,
\[
\begin{eqnarray}
P_{2}&=&\frac {\theta _{\mathrm {A}}-\theta _{\mathrm {C}}}{x_{2}} \\[ 5pt ]
&=&\frac {0.3-0.252}{0.02} \\[ 5pt ]
&=&2.4 \ \mathrm {[p.u.]} \\[ 5pt ]
P_{3}&=&\frac {\theta _{\mathrm {C}}}{x_{3}} \\[ 5pt ]
&=&\frac {0.252}{0.03} \\[ 5pt ]
&=&8.4 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。以上より,発電出力\( \ G_{\mathrm {A}} \ \)及び\( \ G_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
G_{\mathrm {A}}&=&P_{1}+P_{2}+L_{\mathrm {A}} \\[ 5pt ]
&=&6+2.4+10 \\[ 5pt ]
&=&18.4 \ \mathrm {[p.u.]} \\[ 5pt ]
G_{\mathrm {B}}&=&-P_{1}-P_{3}+L_{\mathrm {B}} \\[ 5pt ]
&=&-6-8.4+46 \\[ 5pt ]
&=&31.6 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん