【問題】
【難易度】★★★★★(難しい)
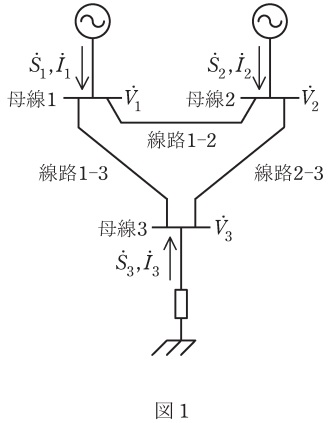
図1の\( \ 3 \ \)母線の電力系統におけるニュートン・ラフソン法を用いた電力潮流計算に関して,次の問に答えよ。
母線\( \ k \ \)から系統に流入する複素電力を\( \ {\dot S}_{k} \ \),母線\( \ k \ \)の電圧を\( \ {\dot V}_{k} \ \)とする。\( \ {\dot S}_{k}=P_{k}+\mathrm {j}Q_{k} \ \)(\( \ P_{k} \ \)は有効電力,\( \ Q_{k} \ \)は無効電力),\( \ {\dot V}_{k}=\left| {\dot V}_{k}\right| \left( \cos \theta _{k}+\mathrm {j}\sin \theta _{k}\right) \ \)である。母線\( \ k \ \)から系統に流入する電流\( \ {\dot I}_{k} \ \)はノードアドミタンス行列\( \ \left[ {\dot Y}_{kl}\right] \ \)を用いて,\( \ {\dot I}_{k}=\displaystyle \sum_{l=1}^3 {\dot Y}_{kl}{\dot V}_{l} \ \)と表すことができる。(\( \ k=1,2,3,l=1,2,3 \ \))
なお,数値は単位法で表し,遅れ無効電力を正とする。
(1) 全ての線路を直列リアクタンス\( \ X_{kl}\left( X_{12},X_{13},X_{23}\right) \ \)のみを考慮した等価回路で表現した場合,\( \ \left[ {\dot Y}_{kl}\right] \ \)を\( \ X_{kl} \ \)で表せ。また,計算過程を簡潔に記せ。
(2) 図1において線路を\( \ \pi \ \)型等価回路で表現し,直列リアクタンス\( \ X_{kl} \ \)に加えて並列キャパシタンス\( \ C_{kl} \ \)を考慮する場合,\( \ \left[ {\dot Y}_{kl}\right] \ \)を表の値を用いて求めよ。なお,\( \ \omega \ \)は系統の角周波数,\( \ C_{kl} / 2 \ \)は線路両端の並列キャパシタンスである。
表
\[
\begin{array}{|c|c|c|}
\hline
k-l & \mathrm {j}X_{kl} & \mathrm {j}\omega C_{kl} / 2 \\
\hline
1-2 & \mathrm {j}0.1 & \mathrm {j}1 \\
1-3 & \mathrm {j}0.1 & \mathrm {j}1 \\
2-3 & \mathrm {j}0.1 & \mathrm {j}1 \\
\hline
\end{array}
\]
(3) 各母線の有効電力,無効電力を電圧の大きさと位相で表す式を電力方程式という。ノードアドミタンス行列の要素を\( \ {\dot Y}_{kl}=G_{kl}+\mathrm {j}B_{kl} \ \)として,\( \ P_{k} \ \),\( \ Q_{k} \ \)を\( \ \left| {\dot V}_{k}\right| \ \),\( \ \left| {\dot V}_{l}\right| \ \),\( \ \theta _{k} \ \),\( \ \theta _{l} \ \),\( \ G_{kl} \ \),\( \ B_{kl} \ \)で表せ。
(4) 小問(2)の\( \ \pi \ \)型等価回路の線路を考える場合,\( \ P_{2} \ \)に関する電力方程式を\( \ \theta _{2} \ \),\( \ \theta _{3} \ \),\( \ \left| {\dot V}_{3}\right| \ \)を用いて示せ。
なお,母線\( \ 1 \ \)では\( \ \theta _{1}=0 \ \),\( \ \left| {\dot V}_{1}\right| =1.0 \ \),母線\( \ 2 \ \)では\( \ P_{2}=0.7 \ \),\( \ \left| {\dot V}_{2}\right| =1.05 \ \)とする。
(5) ニュートン・ラフソン法による潮流計算では,図2のように変数\( \ {\scriptsize {\mathit {\boldsymbol X}}} _{\mathrm {e}} \ \)の推定値を修正し,指定値\( \ {\mathit {\boldsymbol y}} _{\mathrm {s}} \ \)と計算値\( \ {\mathit {\boldsymbol y}} \left( {\scriptsize {\mathit {\boldsymbol X}}} _{\mathrm {e}}\right) \ \)の誤差が十分に小さくなるまで繰り返し計算を行うことで\( \ {\scriptsize {\mathit {\boldsymbol X}}} _{\mathrm {e}} \ \)を求めることができる。ここで,本問において\( \ {\scriptsize {\mathit {\boldsymbol X}}} _{\mathrm {e}} \ \)は,\( \ \theta _{2} \ \),\( \ \theta _{3} \ \),\( \ \left| {\dot V}_{3}\right| \ \)のベクトル,\( \ {\mathit {\boldsymbol y}} \left( {\scriptsize {\mathit {\boldsymbol X}}} _{\mathrm {e}}\right) \ \)は,\( \ {\scriptsize {\mathit {\boldsymbol X}}} _{\mathrm {e}} \ \)によって計算される\( \ P_{2} \ \),\( \ P_{3} \ \),\( \ Q_{3} \ \)のベクトル,\( \ {\mathit {\boldsymbol y}} _{\mathrm {s}} \ \)は,\( \ P_{2} \ \),\( \ P_{3} \ \),\( \ Q_{3} \ \)の与えられた値のベクトルである。\( \ \theta _{2}=0 \ \),\( \ \theta _{3}=0 \ \),\( \ \left| {\dot V}_{3}\right| =1.0 \ \)を初期値とした場合,\( \ 1 \ \)回目の収束計算における\( \ P_{2} \ \)の指定値と計算値との誤差を小問(4)の結果を用いて求めよ。

【ワンポイント解説】
電力の潮流計算に関する問題です。
内容も難しく,解くのにも非常に時間がかかる問題で,多くの受験生を苦しめた問題ではないかと思います。
試験で本問を選択することは現実的ではないため,不要と感じる方は飛ばしてしまっても良いかもしれません。
1.\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路
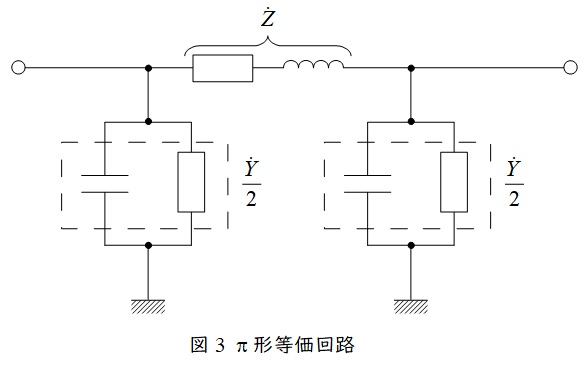
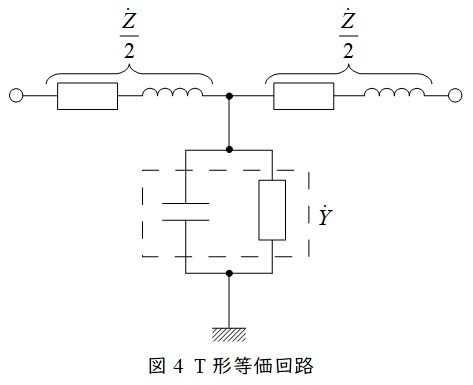
送電線のこう長が大きくなると送電線のリアクタンスや静電容量が無視できなくなるので,\( \ \pi \ \)形等価回路や\( \ \mathrm {T} \ \)形等価回路を適用します。送電線のインピーダンスを\( \ \dot Z \ \),アドミタンスを\( \ \dot Y \ \)とすると,\( \ \pi \ \)形等価回路は図3,\( \ \mathrm {T} \ \)形等価回路は図4のようになります。
電験では送電線の抵抗分やサセプタンス分は無視し,送電線のインダクタンスを\( \ L \ \mathrm {[H]} \ \),静電容量を\( \ C \ \mathrm {[F]} \ \)として,
\[
\begin{eqnarray}
{\dot Z}&=&\mathrm {j}\omega L \\[ 5pt ]
{\dot Y}&=&\mathrm {j}\omega C \\[ 5pt ]
\end{eqnarray}
\]
として扱う問題がほとんどです。
2.複素電力
送電端電圧を\( \ {\dot V}_{\mathrm {s}} \ \),受電端電圧を\( \ {\dot V}_{\mathrm {r}} \ \),送電線電流を\( \ \dot I \ \)とすると,受電端への送電電力\( \ P+\mathrm {j}Q \ \)は遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&{\dot V}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。ただし,\( \ \overline {\dot I} \ \)は\( \ \dot I \ \)の共役複素数であり,\( \ \dot I =I_{\mathrm {r}}+\mathrm {j}I_{\mathrm {i}} \ \)であるとき,\( \ \overline {\dot I}=I_{\mathrm {r}}-\mathrm {j}I_{\mathrm {i}} \ \)となります。
【関連する「電気の神髄」記事】
ニュートン・ラフソン法による潮流計算(理論編)
ニュートン・ラフソン法による潮流計算(実践編)
【解答】
(1)\( \ \left[ {\dot Y}_{kl}\right] \ \)を\( \ X_{kl} \ \)で表す
任意の母線\( \ k \ \)から\( \ l \ \)へ流れる電流を\( \ {\dot I}_{kl} \ \)とする。
題意より,\( \ {\dot I}_{k} \ \)はノードアドミタンス行列\( \ \left[ {\dot Y}_{kl}\right] \ \)を用いて,\( \ {\dot I}_{k}=\displaystyle \sum_{l=1}^3 {\dot Y}_{kl}{\dot V}_{l} \ \)の関係があり,図1より,
\[
\begin{eqnarray}
{\dot I}_{1}&=&{\dot I}_{12}+{\dot I}_{13} \\[ 5pt ]
&=&\frac {{\dot V}_{1}-{\dot V}_{2}}{\mathrm {j}X_{12}}+\frac {{\dot V}_{1}-{\dot V}_{3}}{\mathrm {j}X_{13}} \\[ 5pt ]
&=&\left( \frac {1}{\mathrm {j}X_{12}}+\frac {1}{\mathrm {j}X_{13}}\right) {\dot V}_{1}-\frac {1}{\mathrm {j}X_{12}}{\dot V}_{2}-\frac {1}{\mathrm {j}X_{13}}{\dot V}_{3} \\[ 5pt ]
{\dot I}_{2}&=&{\dot I}_{21}+{\dot I}_{23} \\[ 5pt ]
&=&\frac {{\dot V}_{2}-{\dot V}_{1}}{\mathrm {j}X_{12}}+\frac {{\dot V}_{2}-{\dot V}_{3}}{\mathrm {j}X_{23}} \\[ 5pt ]
&=&-\frac {1}{\mathrm {j}X_{12}}{\dot V}_{1}+\left( \frac {1}{\mathrm {j}X_{12}}+\frac {1}{\mathrm {j}X_{23}}\right) {\dot V}_{2}-\frac {1}{\mathrm {j}X_{23}}{\dot V}_{3} \\[ 5pt ]
{\dot I}_{3}&=&{\dot I}_{31}+{\dot I}_{32} \\[ 5pt ]
&=&\frac {{\dot V}_{3}-{\dot V}_{1}}{\mathrm {j}X_{13}}+\frac {{\dot V}_{3}-{\dot V}_{2}}{\mathrm {j}X_{23}} \\[ 5pt ]
&=&-\frac {1}{\mathrm {j}X_{13}}{\dot V}_{1}-\frac {1}{\mathrm {j}X_{23}}{\dot V}_{2}+\left( \frac {1}{\mathrm {j}X_{13}}+\frac {1}{\mathrm {j}X_{23}}\right) {\dot V}_{3} \\[ 5pt ]
\end{eqnarray}
\]
となり,これを行列式の形に整理すると,
\[
\begin{eqnarray}
\begin{bmatrix}
{\dot I}_{1} \\
{\dot I}_{2} \\
{\dot I}_{3} \\
\end{bmatrix}
&=&
\begin{bmatrix}
\displaystyle \frac {1}{\mathrm {j}X_{12}}+\frac {1}{\mathrm {j}X_{13}} & \displaystyle -\frac {1}{\mathrm {j}X_{12}} & \displaystyle -\frac {1}{\mathrm {j}X_{13}} \\
\displaystyle -\frac {1}{\mathrm {j}X_{12}} & \displaystyle \frac {1}{\mathrm {j}X_{12}}+\frac {1}{\mathrm {j}X_{23}} & \displaystyle -\frac {1}{\mathrm {j}X_{23}} \\
\displaystyle -\frac {1}{\mathrm {j}X_{13}} & \displaystyle -\frac {1}{\mathrm {j}X_{23}} & \displaystyle \frac {1}{\mathrm {j}X_{13}}+\frac {1}{\mathrm {j}X_{23}} \\
\end{bmatrix}
\begin{bmatrix}
{\dot V}_{1} \\
{\dot V}_{2} \\
{\dot V}_{3} \\
\end{bmatrix}
\end{eqnarray}
\]
となるので,ノードアドミタンス行列\( \ \left[ {\dot Y}_{kl}\right] \ \)は,
\[
\begin{eqnarray}
\left[ {\dot Y}_{kl}\right]
&=&
\begin{bmatrix}
\displaystyle \frac {1}{\mathrm {j}X_{12}}+\frac {1}{\mathrm {j}X_{13}} & \displaystyle -\frac {1}{\mathrm {j}X_{12}} & \displaystyle -\frac {1}{\mathrm {j}X_{13}} \\
\displaystyle -\frac {1}{\mathrm {j}X_{12}} & \displaystyle \frac {1}{\mathrm {j}X_{12}}+\frac {1}{\mathrm {j}X_{23}} & \displaystyle -\frac {1}{\mathrm {j}X_{23}} \\
\displaystyle -\frac {1}{\mathrm {j}X_{13}} & \displaystyle -\frac {1}{\mathrm {j}X_{23}} & \displaystyle \frac {1}{\mathrm {j}X_{13}}+\frac {1}{\mathrm {j}X_{23}} \\
\end{bmatrix}
\end{eqnarray}
\]
と求められる。
(2)線路を\( \ \pi \ \)型等価回路で表現し,直列リアクタンス\( \ X_{kl} \ \)に加えて並列キャパシタンス\( \ C_{kl} \ \)を考慮する場合,\( \ \left[ {\dot Y}_{kl}\right] \ \)を表の値を用いて求める
ワンポイント解説「1.\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路」の通り,\( \ \pi \ \)形等価回路においては,線路の端にキャパシタンスが追加されると考えられ,各電流は並列キャパシタンス分の電流が上乗せされるので,(1)と同様に求めると,
\[
\begin{eqnarray}
{\dot I}_{1}&=&{\dot I}_{12}+{\dot I}_{13}+{\dot I}_{\mathrm {C1}} \\[ 5pt ]
&=&\frac {{\dot V}_{1}-{\dot V}_{2}}{\mathrm {j}X_{12}}+\frac {{\dot V}_{1}-{\dot V}_{3}}{\mathrm {j}X_{13}}+\left( \frac {\mathrm {j}\omega C_{12}}{2}+\frac {\mathrm {j}\omega C_{13}}{2}\right) {\dot V}_{1} \\[ 5pt ]
&=&\left( \frac {1}{\mathrm {j}X_{12}}+\frac {1}{\mathrm {j}X_{13}}+\frac {\mathrm {j}\omega C_{12}}{2}+\frac {\mathrm {j}\omega C_{13}}{2}\right) {\dot V}_{1}-\frac {1}{\mathrm {j}X_{12}}{\dot V}_{2}-\frac {1}{\mathrm {j}X_{13}}{\dot V}_{3} \\[ 5pt ]
{\dot I}_{2}&=&{\dot I}_{21}+{\dot I}_{23}+{\dot I}_{\mathrm {C2}} \\[ 5pt ]
&=&\frac {{\dot V}_{2}-{\dot V}_{1}}{\mathrm {j}X_{12}}+\frac {{\dot V}_{2}-{\dot V}_{3}}{\mathrm {j}X_{23}}+\left( \frac {\mathrm {j}\omega C_{12}}{2}+\frac {\mathrm {j}\omega C_{23}}{2}\right) {\dot V}_{2} \\[ 5pt ]
&=&-\frac {1}{\mathrm {j}X_{12}}{\dot V}_{1}+\left( \frac {1}{\mathrm {j}X_{12}}+\frac {1}{\mathrm {j}X_{23}}+\frac {\mathrm {j}\omega C_{12}}{2}+\frac {\mathrm {j}\omega C_{23}}{2}\right) {\dot V}_{2}-\frac {1}{\mathrm {j}X_{23}}{\dot V}_{3} \\[ 5pt ]
{\dot I}_{3}&=&{\dot I}_{31}+{\dot I}_{32}+{\dot I}_{\mathrm {C3}} \\[ 5pt ]
&=&\frac {{\dot V}_{3}-{\dot V}_{1}}{\mathrm {j}X_{13}}+\frac {{\dot V}_{3}-{\dot V}_{2}}{\mathrm {j}X_{23}}+\left( \frac {\mathrm {j}\omega C_{13}}{2}+\frac {\mathrm {j}\omega C_{23}}{2}\right) {\dot V}_{3} \\[ 5pt ]
&=&-\frac {1}{\mathrm {j}X_{13}}{\dot V}_{1}-\frac {1}{\mathrm {j}X_{23}}{\dot V}_{2}+\left( \frac {1}{\mathrm {j}X_{13}}+\frac {1}{\mathrm {j}X_{23}}+\frac {\mathrm {j}\omega C_{13}}{2}+\frac {\mathrm {j}\omega C_{23}}{2}\right) {\dot V}_{3} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ノードアドミタンス行列\( \ \left[ {\dot Y}_{kl}\right] \ \)は,
\[
\begin{eqnarray}
\left[ {\dot Y}_{kl}\right]
&=&
\begin{bmatrix}
\displaystyle \frac {1}{\mathrm {j}X_{12}}+\frac {1}{\mathrm {j}X_{13}}+\frac {\mathrm {j}\omega C_{12}}{2}+\frac {\mathrm {j}\omega C_{13}}{2} & \displaystyle -\frac {1}{\mathrm {j}X_{12}} & \displaystyle -\frac {1}{\mathrm {j}X_{13}} \\
\displaystyle -\frac {1}{\mathrm {j}X_{12}} & \displaystyle \frac {1}{\mathrm {j}X_{12}}+\frac {1}{\mathrm {j}X_{23}}+\frac {\mathrm {j}\omega C_{12}}{2}+\frac {\mathrm {j}\omega C_{23}}{2} & \displaystyle -\frac {1}{\mathrm {j}X_{23}} \\
\displaystyle -\frac {1}{\mathrm {j}X_{13}} & \displaystyle -\frac {1}{\mathrm {j}X_{23}} & \displaystyle \frac {1}{\mathrm {j}X_{13}}+\frac {1}{\mathrm {j}X_{23}}+\frac {\mathrm {j}\omega C_{13}}{2}+\frac {\mathrm {j}\omega C_{23}}{2} \\
\end{bmatrix}
\end{eqnarray}
\]
となり,各値を代入すると,
\[
\begin{eqnarray}
\left[ {\dot Y}_{kl}\right]
&=&
\begin{bmatrix}
\displaystyle \frac {1}{\mathrm {j}0.1}+\frac {1}{\mathrm {j}0.1}+\mathrm {j}1+\mathrm {j}1 & \displaystyle -\frac {1}{\mathrm {j}0.1} & \displaystyle -\frac {1}{\mathrm {j}0.1} \\
\displaystyle -\frac {1}{\mathrm {j}0.1} & \displaystyle \frac {1}{\mathrm {j}0.1}+\frac {1}{\mathrm {j}0.1}+\mathrm {j}1+\mathrm {j}1 & \displaystyle -\frac {1}{\mathrm {j}0.1} \\
\displaystyle -\frac {1}{\mathrm {j}0.1} & \displaystyle -\frac {1}{\mathrm {j}0.1} & \displaystyle \frac {1}{\mathrm {j}0.1}+\frac {1}{\mathrm {j}0.1}+\mathrm {j}1+\mathrm {j}1 \\
\end{bmatrix} \\[ 5pt ]
&=&
\begin{bmatrix}
-\mathrm {j}18 & \mathrm {j}10 & \mathrm {j}10 \\
\mathrm {j}10 & -\mathrm {j}18 & \mathrm {j}10 \\
\mathrm {j}10 & \mathrm {j}10 & -\mathrm {j}18 \\
\end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ P_{k} \ \),\( \ Q_{k} \ \)を\( \ \left| {\dot V}_{k}\right| \ \),\( \ \left| {\dot V}_{l}\right| \ \),\( \ \theta _{k} \ \),\( \ \theta _{l} \ \),\( \ G_{kl} \ \),\( \ B_{kl} \ \)で表す
ワンポイント解説「2.複素電力」の通り,遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P_{k}+\mathrm {j}Q_{k}&=&{\dot V}_{\mathrm {k}}\overline {\dot I_{k}} \\[ 5pt ]
&=&{\dot V}_{\mathrm {k}}\displaystyle \sum_{l=1}^3 \overline {{\dot Y}_{kl}{\dot V}_{l}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,
\[
\begin{eqnarray}
{\dot V}_{k}&=&\left| {\dot V}_{k}\right| \left( \cos \theta _{k}+\mathrm {j}\sin \theta _{k}\right) \\[ 5pt ]
\overline {{\dot V}_{l}}&=&\left| {\dot V}_{l}\right| \left( \cos \theta _{l}-\mathrm {j}\sin \theta _{l}\right) \\[ 5pt ]
\overline {{\dot Y}_{kl}}&=&G_{kl}-\mathrm {j}B_{kl} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
P_{k}+\mathrm {j}Q_{k}&=&\left| {\dot V}_{k}\right| \left( \cos \theta _{k}+\mathrm {j}\sin \theta _{k}\right)\displaystyle \sum_{l=1}^3 \left( G_{kl}-\mathrm {j}B_{kl}\right) \left| {\dot V}_{l}\right| \left( \cos \theta _{l}-\mathrm {j}\sin \theta _{l}\right) \\[ 5pt ]
&=&\displaystyle \sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left( \cos \theta _{k}+\mathrm {j}\sin \theta _{k}\right) \left( \cos \theta _{l}-\mathrm {j}\sin \theta _{l}\right) \left( G_{kl}-\mathrm {j}B_{kl}\right) \\[ 5pt ]
&=&\displaystyle \sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left\{ \cos \theta _{k}\cos \theta _{l}+\sin \theta _{k}\sin \theta _{l}+\mathrm {j}\left( \sin \theta _{k}\cos \theta _{l}-\cos \theta _{k}\sin \theta _{l}\right) \right\} \left( G_{kl}-\mathrm {j}B_{kl}\right) \\[ 5pt ]
&=&\displaystyle \sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left\{ \cos \left( \theta _{k}- \theta _{l}\right) +\mathrm {j} \sin \left( \theta _{k}- \theta _{l}\right) \right\} \left( G_{kl}-\mathrm {j}B_{kl}\right) \\[ 5pt ]
&=&\displaystyle \sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left[ G_{kl} \cos \left( \theta _{k}- \theta _{l}\right) +B_{kl}\sin \left( \theta _{k}- \theta _{l}\right) +\mathrm {j} \left\{ G_{kl} \sin \left( \theta _{k}- \theta _{l}\right) -B_{kl}\cos \left( \theta _{k}- \theta _{l}\right) \right\} \right] \\[ 5pt ]
\end{eqnarray}
\]
と整理できるので,\( \ P_{k} \ \)及び\( \ Q_{k} \ \)は,
\[
\begin{eqnarray}
P_{k}&=&\sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left\{ G_{kl} \cos \left( \theta _{k}- \theta _{l}\right) +B_{kl}\sin \left( \theta _{k}- \theta _{l}\right) \right\} \\[ 5pt ]
Q_{k}&=&\sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left\{ G_{kl} \sin \left( \theta _{k}- \theta _{l}\right) -B_{kl}\cos \left( \theta _{k}- \theta _{l}\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ P_{2} \ \)に関する電力方程式を\( \ \theta _{2} \ \),\( \ \theta _{3} \ \),\( \ \left| {\dot V}_{3}\right| \ \)を用いて示す
(3)解答式に\( \ k=2 \ \)を代入すると,
\[
\begin{eqnarray}
P_{2}&=&\sum_{l=1}^3\left| {\dot V}_{2}\right| \left| {\dot V}_{l}\right| \left\{ G_{2l} \cos \left( \theta _{2}- \theta _{l}\right) +B_{2l}\sin \left( \theta _{2}- \theta _{l}\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より任意の\( \ G_{2l}=0 \ \)であるから,
\[
\begin{eqnarray}
P_{2}&=&\sum_{l=1}^3\left| {\dot V}_{2}\right| \left| {\dot V}_{l}\right| B_{2l}\sin \left( \theta _{2}- \theta _{l}\right) \\[ 5pt ]
&=&\left| {\dot V}_{2}\right| \left| {\dot V}_{1}\right| B_{21}\sin \left( \theta _{2}- \theta _{1}\right) +\left| {\dot V}_{2}\right| ^{2} B_{22}\sin \left( \theta _{2}- \theta _{2}\right) +\left| {\dot V}_{2}\right| \left| {\dot V}_{3}\right| B_{23}\sin \left( \theta _{2}- \theta _{3}\right) \\[ 5pt ]
&=&\left| {\dot V}_{2}\right| \left| {\dot V}_{1}\right| B_{21}\sin \left( \theta _{2}- \theta _{1}\right) +\left| {\dot V}_{2}\right| \left| {\dot V}_{3}\right| B_{23}\sin \left( \theta _{2}- \theta _{3}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,各値を代入すると,
\[
\begin{eqnarray}
0.7&=&1.05\times 1.0 \times 10 \sin \left( \theta _{2}- 0\right) +1.05 \left| {\dot V}_{3}\right| \times 10 \sin \left( \theta _{2}- \theta _{3}\right) \\[ 5pt ]
&=&10.5 \sin \theta _{2} +10.5 \left| {\dot V}_{3}\right| \sin \left( \theta _{2}- \theta _{3}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ \theta _{2}=0 \ \),\( \ \theta _{3}=0 \ \),\( \ \left| {\dot V}_{3}\right| =1.0 \ \)を初期値とした場合,\( \ 1 \ \)回目の収束計算における\( \ P_{2} \ \)の指定値と計算値との誤差を求める
図2に沿って\( \ P_{2} \ \)の計算値\( \ P_{2}\left( {\scriptsize {\mathit {\boldsymbol X}}} _{\mathrm {e}}\right) \ \)を求めると,
\[
\begin{eqnarray}
P_{2}\left( {\scriptsize {\mathit {\boldsymbol X}}} _{\mathrm {e}}\right) &=&10.5 \sin \theta _{2} +10.5 \left| {\dot V}_{3}\right| \sin \left( \theta _{2}- \theta _{3}\right) \\[ 5pt ]
&=&10.5 \sin 0 +10.5 \times 1.0 \sin \left( 0- 0\right) \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ P_{2} \ \)の指定値\( \ P_{2\mathrm {s}}=0.7 \ \)であるから,その誤差\( \ \Delta P_{2} \ \)は,
\[
\begin{eqnarray}
\Delta P_{2} &=&P_{2\mathrm {s}}-P_{2}\left( {\scriptsize {\mathit {\boldsymbol X}}} _{\mathrm {e}}\right) \\[ 5pt ]
&=&0.7-0 \\[ 5pt ]
&=&0.7 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん