【問題】
【難易度】★★☆☆☆(やや易しい)
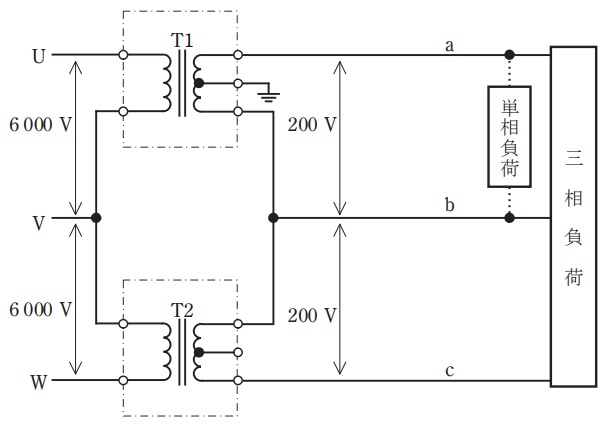
図は,\( \ 1 \ \)次電圧\( \ 6 \ \mathrm {kV} \ \),\( \ 2 \ \)次電圧\( \ 200 \ \mathrm {V} \ \)の単相変圧器\( \ 2 \ \)台を用いて単相負荷及び三相負荷に電力を供給する回路である。次の問に答えよ。ただし,変圧器\( \ 1 \ \)次側電圧は平衡三相\( \ 6 \ \mathrm {kV} \ \)に維持され,三相負荷は平衡であるとする。無効電力の向きは,遅れ消費側を正とする。変圧器のインピーダンスは,無視してよい。相回転の順序は\( \ \mathrm {a} \ \),\( \ \mathrm {b} \ \),\( \ \mathrm {c} \ \)とする。
(1) 三相負荷だけに供給しているとする。三相負荷の容量が\( \ 30 \ \mathrm {kV\cdot A} \ \)であるとき,変圧器\( \ \mathrm {T1} \ \),変圧器\( \ \mathrm {T2} \ \)が供給する皮相電力を求めよ。
(2) 小問(1)で三相負荷の力率角が遅れ\( \ 30° \ \)のとき,変圧器\( \ \mathrm {T1} \ \)が供給する有効電力と無効電力,並びに変圧器\( \ \mathrm {T2} \ \)が供給する有効電力と無効電力をそれぞれ求めよ。
(3) 小問(2)に\( \ 8.66 \ \mathrm {kV\cdot A} \ \),進み力率角\( \ 60° \ \)の単相負荷の需要家が追加となった。そのときの変圧器\( \ \mathrm {T1} \ \)が供給する有効電力と皮相電力をそれぞれ求めよ。
【ワンポイント解説】
異容量\( \ \mathrm {V} \ \)結線方式による三相負荷と単相負荷への電力供給に関する計算問題です。
ベクトル図を描き各変圧器の容量を求める,異容量\( \ \mathrm {V} \ \)結線方式を理解する上ではとても良い問題と言えます。
問3と共に\( \ 1 \ \)種合格に向けてはできれば完答を目指したい問題です。
1.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較
①\( \ \mathrm {\Delta -\Delta } \ \)結線
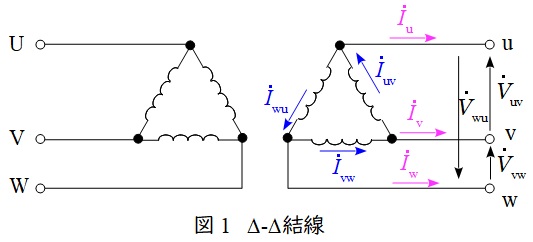
\( \ \mathrm {\Delta -\Delta } \ \)結線の変圧器の回路図とベクトル図を図1及び図2に示します。
図1において,負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \)は,変圧器を流れる電流\( \ {\dot I}_{\mathrm {uv}} \ \mathrm {[A]} \ \)及び\( \ {\dot I}_{\mathrm {wu}} \ \mathrm {[A]} \ \)を用いて,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}}-{\dot I}_{\mathrm {wu}} \\[ 5pt ]
\end{eqnarray}
\]
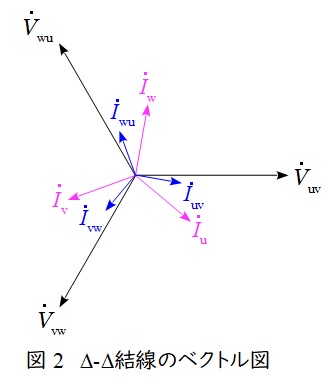
で求められ,ベクトル図上では図2のような関係となり,三相平衡である場合にはそれぞれの大きさの比は,
\[
\begin{eqnarray}
I_{\mathrm {u}}&=& \sqrt {3}I_{\mathrm {uv}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって,各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は,負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \),負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると,
\[
\begin{eqnarray}
S&=& \frac {VI}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
となります。したがって,変圧器全体の送電電力\( \ P \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P&=& 3S\cos \theta \\[ 5pt ]
&=& 3\cdot \frac {VI}{\sqrt {3}}\cdot \cos \theta \\[ 5pt ]
&=&\sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
②\( \ \mathrm {V -V } \ \)結線
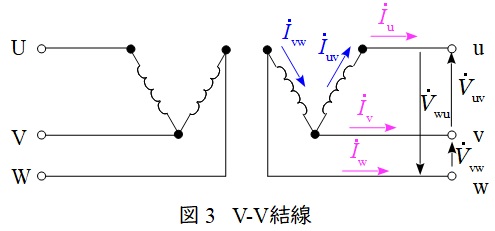
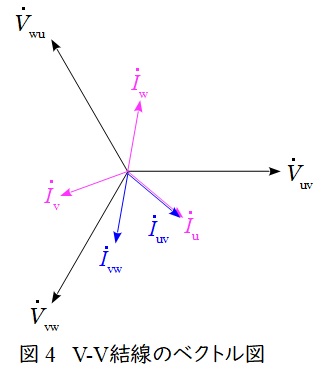
\( \ \mathrm {V -V } \ \)結線の変圧器の回路図とベクトル図を図3及び図4に示します。
図3において,負荷電流\( \ {\dot I}_{\mathrm {u}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {v}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {w}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {u}}&=& {\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {v}}&=& {\dot I}_{\mathrm {vw}}-{\dot I}_{\mathrm {uv}} \\[ 5pt ]
{\dot I}_{\mathrm {w}}&=& -{\dot I}_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
で求められ,ベクトル図上では図4のような関係となり,三相平衡である場合にはそれぞれの大きさの比は,
\[
\begin{eqnarray}
I_{\mathrm {u}}&=&I_{\mathrm {v}}&=&I_{\mathrm {w}}&=&I_{\mathrm {uv}}&=&I_{\mathrm {vw}} \\[ 5pt ]
\end{eqnarray}
\]
であることが分かります。したがって,各変圧器が分担する容量\( \ S \ \mathrm {[V\cdot A]} \ \)は,負荷の線間電圧を\( \ V_{\mathrm {uv}}=V_{\mathrm {vw}}=V_{\mathrm {wu}}=V \ \),負荷電流を\( \ I_{\mathrm {u}}=I_{\mathrm {v}}=I_{\mathrm {w}}=I \ \)とすると,
\[
\begin{eqnarray}
S&=& VI \\[ 5pt ]
\end{eqnarray}
\]
となります。変圧器全体の送電電力\( \ P_{\mathrm {V}} \ \mathrm {[W]} \ \)は力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P_{\mathrm {V}}&=& \sqrt {3}VI \cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \mathrm {V -V } \ \)結線で得られる出力\( \ \mathrm {[V\cdot A]} \ \)は各変圧器の出力の\( \ \sqrt {3} \ \)倍となるため,利用率は,
\[
\begin{eqnarray}
利用率&=& \frac {\sqrt {3}VI}{2VI} \\[ 5pt ]
&=& \frac {\sqrt {3}}{2} → 86.6 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,\( \ \mathrm {V -V } \ \)結線と\( \ \mathrm {\Delta -\Delta } \ \)結線で同じ電力を出力する場合に必要となる変圧器の容量比は,
\[
\begin{eqnarray}
容量比&=& \frac {\displaystyle \frac {VI}{\sqrt {3}}}{VI} \\[ 5pt ]
&=& \frac {1}{\sqrt {3}} → 57.7 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となるため,\( \ \mathrm {V -V } \ \)結線の出力は\( \ \mathrm {\Delta -\Delta } \ \)結線の\( \ 57.7 \ \mathrm {[%]} \ \)程度であることがわかります。
【解答】
(1)変圧器\( \ \mathrm {T1} \ \),変圧器\( \ \mathrm {T2} \ \)が供給する皮相電力
三相負荷の皮相電力\( \ S_{3} \ \mathrm {[V\cdot A]} \ \)は,各変圧器の二次電圧\( \ V \ \mathrm {[V]} \ \),二次電流\( \ I \ \mathrm {[A]} \ \)を用いて,
\[
\begin{eqnarray}
S_{3}&=& \sqrt {3}VI \\[ 5pt ]
\end{eqnarray}
\]
となり,変圧器\( \ \mathrm {T1} \ \),変圧器\( \ \mathrm {T2} \ \)の皮相電力\( \ S_{\mathrm {T}} \ \mathrm {[V\cdot A]} \ \)は,ワンポイント解説「1.\( \ \mathrm {\Delta -\Delta } \ \)結線と\( \ \mathrm {V-V} \ \)結線の比較」の通り,
\[
\begin{eqnarray}
S_{\mathrm {T}}&=& VI \\[ 5pt ]
&=& \frac {S_{3}}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,三相負荷の皮相電力\( \ S_{3}=30 \ \mathrm {[kV\cdot A]} \ \)であるから,皮相電力\( \ S_{\mathrm {T}} \ \mathrm {[kV\cdot A]} \ \)は,
\[
\begin{eqnarray}
S_{\mathrm {T}}&=& \frac {S_{3}}{\sqrt {3}} \\[ 5pt ]
&=& \frac {30}{\sqrt {3}} \\[ 5pt ]
&≒& 17.321 → 17.3 \ \mathrm {[kV\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)三相負荷の力率角が遅れ\( \ 30° \ \)のとき,変圧器\( \ \mathrm {T1} \ \)が供給する有効電力と無効電力,並びに変圧器\( \ \mathrm {T2} \ \)が供給する有効電力と無効電力
力率角が遅れ\( \ 30° \ \)のときの三相負荷のベクトル図は,\( \ \mathrm {a} \ \)相,\( \ \mathrm {b} \ \)相,\( \ \mathrm {c} \ \)相のそれぞれの相電圧\( \ {\dot E}_{\mathrm {a}} \ \mathrm {[V]} \ \),\( \ {\dot E}_{\mathrm {b}} \ \mathrm {[V]} \ \),\( \ {\dot E}_{\mathrm {c}} \ \mathrm {[V]} \ \),それぞれの線電流\( \ {\dot I}_{\mathrm {a}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {b}} \ \mathrm {[A]} \ \),\( \ {\dot I}_{\mathrm {c}} \ \mathrm {[A]} \ \)とすると図5のようになる。変圧器\( \ \mathrm {T1} \ \)の電圧\( \ {\dot V}_{\mathrm {1}} \ \mathrm {[V]} \ \)及び電流\( \ {\dot I}_{\mathrm {1}} \ \mathrm {[A]} \ \),変圧器\( \ \mathrm {T2} \ \)の電圧\( \ {\dot V}_{\mathrm {2}} \ \mathrm {[V]} \ \)及び電流\( \ {\dot I}_{\mathrm {2}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {1}}&=& {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}} \\[ 5pt ]
{\dot I}_{\mathrm {1}}&=& {\dot I}_{\mathrm {a}} \\[ 5pt ]
{\dot V}_{\mathrm {2}}&=& {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}} \\[ 5pt ]
{\dot I}_{\mathrm {2}}&=& -{\dot I}_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
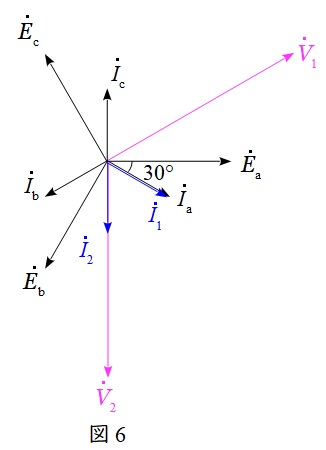
であるから,\( \ {\dot V}_{\mathrm {1}} \ \mathrm {[V]} \ \),\( \ {\dot I}_{\mathrm {1}} \ \mathrm {[A]} \ \),\( \ {\dot V}_{\mathrm {2}} \ \mathrm {[V]} \ \),\( \ {\dot I}_{\mathrm {2}} \ \mathrm {[A]} \ \)を含めたベクトル図は図6のようになる。また,各相の線電流の大きさ\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
S_{3}&=& \sqrt {3}VI \\[ 5pt ]
I&=&\frac {S_{3}}{\sqrt {3}V} \\[ 5pt ]
&=&\frac {30\times 10^{3}}{\sqrt {3}\times 200} \\[ 5pt ]
&=&86.603 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であり,図6より\( \ {\dot V}_{\mathrm {1}} \ \mathrm {[V]} \ \)と\( \ {\dot I}_{\mathrm {1}} \ \mathrm {[A]} \ \)のなす角が\( \ 60° \ \),\( \ {\dot V}_{\mathrm {2}} \ \mathrm {[V]} \ \)と\( \ {\dot I}_{\mathrm {2}} \ \mathrm {[A]} \ \)のなす角が\( \ 0° \ \)であることから,変圧器\( \ \mathrm {T1} \ \)が供給する有効電力\( \ P_{\mathrm {1}} \ \mathrm {[kW]} \ \)と無効電力\( \ Q_{\mathrm {1}} \ \mathrm {[kvar]} \ \),並びに変圧器\( \ \mathrm {T2} \ \)が供給する有効電力\( \ P_{\mathrm {2}} \ \mathrm {[kW]} \ \)及び無効電力\( \ Q_{\mathrm {2}} \ \mathrm {[kvar]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {1}}&=& VI\cos 60° \\[ 5pt ]
&=& 200\times 86.603 \times \frac {1}{2} \\[ 5pt ]
&≒&8 \ 660.3 \ \mathrm {[W]} → 8.66 \ \mathrm {[kW]} \\[ 5pt ]
Q_{\mathrm {1}}&=& VI\sin 60° \\[ 5pt ]
&=& 200\times 86.603 \times \frac {\sqrt {3}}{2} \\[ 5pt ]
&≒&15 \ 000 \ \mathrm {[var]} → 15.0 \ \mathrm {[kvar]} \\[ 5pt ]
P_{\mathrm {2}}&=& VI\cos 0° \\[ 5pt ]
&=& 200\times 86.603 \times 1 \\[ 5pt ]
&≒&17 \ 321 \ \mathrm {[W]} → 17.3 \ \mathrm {[kW]} \\[ 5pt ]
Q_{\mathrm {2}}&=& VI\sin 0° \\[ 5pt ]
&=& 200\times 86.603 \times 0 \\[ 5pt ]
&=&0 \ \mathrm {[var]} → 0 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。

(3)\( \ 8.66 \ \mathrm {kV\cdot A} \ \),進み力率角\( \ 60° \ \)の単相負荷の需要家が追加となったときの変圧器\( \ \mathrm {T1} \ \)が供給する有効電力と皮相電力
\( \ S_{\mathrm {1}}=8.66 \ \mathrm {[kV\cdot A]} \ \)の単相負荷の電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \)の大きさは,
\[
\begin{eqnarray}
S_{\mathrm {1}}&=& VI_{\mathrm {s}} \\[ 5pt ]
I_{\mathrm {s}}&=&\frac {S_{\mathrm {1}}}{V} \\[ 5pt ]
&=&\frac {8.66\times 10^{3}}{200} \\[ 5pt ]
&=&43.3 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
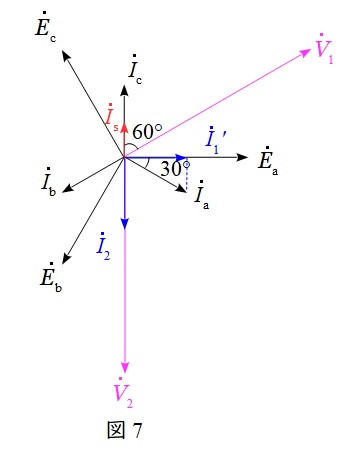
であり,\( \ \displaystyle I_{\mathrm {s}}=\frac {1}{2}I_{\mathrm {a}} \ \)に注意してベクトル図を描くと図7のようになる。よって,このときの変圧器\( \ \mathrm {T1} \ \)の電流\( \ I_{\mathrm {1}}^{\prime } \ \mathrm {[A]} \ \)の大きさは,
\[
\begin{eqnarray}
I_{\mathrm {1}}^{\prime }&=&\sqrt {3}I_{\mathrm {s}} \\[ 5pt ]
&=&\sqrt {3}\times 43.3 \\[ 5pt ]
&≒&74.998 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,変圧器\( \ \mathrm {T1} \ \)が供給する有効電力\( \ P_{\mathrm {1}}^{\prime } \ \mathrm {[kW]} \ \)と皮相電力\( \ S_{\mathrm {1}}^{\prime } \ \mathrm {[kV\cdot A]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {1}}^{\prime }&=& VI_{\mathrm {1}}^{\prime }\cos 30° \\[ 5pt ]
&=& 200\times 74.998 \times \frac {\sqrt {3}}{2} \\[ 5pt ]
&≒&12 \ 990 \ \mathrm {[W]} → 13.0 \ \mathrm {[kW]} \\[ 5pt ]
S_{\mathrm {1}}^{\prime }&=& VI_{\mathrm {1}}^{\prime } \\[ 5pt ]
&=& 200\times 74.998 \\[ 5pt ]
&≒&15 \ 000 \ \mathrm {[V\cdot A]} → 15.0 \ \mathrm {[kV\cdot A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん