【問題】
【難易度】★★★★☆(やや難しい)
図1の抵抗\( \ R \ \)とリアクタンス\( \ X \ \)で表される送電線の特性について電力円線図を用いて考える。なお,本問において単位のない諸量は単位法で表されており,受電端電圧\( \ {\dot E}_{\mathrm {r}} \ \)の位相を零,送電端電圧\( \ {\dot E}_{\mathrm {s}} \ \)の位相を\( \ \delta \ \mathrm {[rad]} \ \left( 0≦\delta ≦\pi -\alpha \right) \ \)とする。次の問に答えよ。
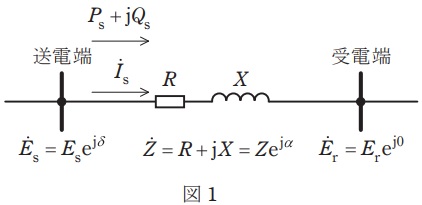
(1) 送電端円線図の式を次の手順で求めよ。
a) 送電端から流れ出す電流\( \ {\dot I}_{\mathrm {s}} \ \)を\( \ {\dot E}_{\mathrm {s}} \ \),\( \ {\dot E}_{\mathrm {r}} \ \),\( \ \dot Z \ \)を用いて表せ。
b) 送電端から流れ出す有効電力\( \ P_{\mathrm {s}} \ \),無効電力\( \ Q_{\mathrm {s}} \ \)を\( \ E_{\mathrm {s}} \ \),\( \ E_{\mathrm {r}} \ \),\( \ Z \ \),\( \ \alpha \ \),\( \ \delta \ \)を用いて表せ。
c) 送電端円線図の式を\( \ P_{\mathrm {s}} \ \),\( \ Q_{\mathrm {s}} \ \)を用いて,\( \ \left( P_{\mathrm {s}}-x_{\mathrm {1}}\right) ^{2} +\left( Q_{\mathrm {s}}-x_{\mathrm {2}}\right) ^{2}={x_{\mathrm {3}}}^{2} \ \)と表したとき,送電端円線図の中心\( \ \left( x_{\mathrm {1}},x_{\mathrm {2}}\right) \ \),半径\( \ x_{3} \ \)を\( \ E_{\mathrm {s}} \ \),\( \ E_{\mathrm {r}} \ \),\( \ Z \ \),\( \ \alpha \ \)を用いて表せ。なお,\( \ \sin ^{2} \left( \delta +\alpha \right) +\cos ^{2} \left( \delta +\alpha \right) =1 \ \)を用いてもよい。
(2) 答案用紙に印刷されている図2に受電端円線図を描き,有効電力損失,無効電力損失を図中で示せ。なお,受電端円線図は,\( \ E_{\mathrm {s}}=E_{\mathrm {r}} \ \)として,二つの円の中心と原点の位置関係,二つの円の交差に留意して描くこと。
(3) 図1の送電線\( \ 1 \ \)相当たりの抵抗が\( \ 5 \ \mathrm {\Omega } \ \),リアクタンスが\( \ 20 \ \mathrm {\Omega } \ \),送電端電圧と受電端電圧が\( \ 500 \ \mathrm {kV} \ \)の場合,単位法の基準容量を\( \ 1 \ 000 \ \mathrm {MV\cdot A} \ \),基準電圧を\( \ 500 \ \mathrm {kV} \ \)として,送電端円線図の中心と半径を単位法で求めよ。
【ワンポイント解説】
送電線の電力円線図に関する問題です。
抵抗分を考慮にいれ,計算量を増やしているのが\( \ 1 \ \)種らしい問題と言えます。
本問自体はかなり難易度が高いので,本番で選択するのは合理的な選択ではない気はしますが,電力円線図の考え方において非常に良い勉強となりますので,ぜひ理解するようにして下さい。
1.オイラーの公式
複素計算で用いるオイラーの公式は以下の通りとなります。こちらは覚えるようにしましょう。
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ]
\mathrm {e}^{\mathrm {-j}\theta }&=&\cos \theta -\mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
2.複素電力
三相線路において,送電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[V]} \ \),受電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {r}} \ \mathrm {[V]} \ \),送電線電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると,受電端への送電電力\( \ P+\mathrm {j}Q \ \mathrm {[V\cdot A]} \ \)は遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&3{\dot E}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。ただし,\( \ \overline {\dot I} \ \)は\( \ \dot I \ \)の共役複素数であり,\( \ \dot I =I_{\mathrm {r}}+\mathrm {j}I_{\mathrm {i}} \ \)であるとき,\( \ \overline {\dot I}=I_{\mathrm {r}}-\mathrm {j}I_{\mathrm {i}} \ \)となります。
ここで,基準容量を\( P_{\mathrm {n}}=3E_{\mathrm {n}}I_{\mathrm {n}} \ \)としたとき,単位法での複素電力は,
\[
\begin{eqnarray}
\frac {P}{3E_{\mathrm {n}}I_{\mathrm {n}}}+\mathrm {j}\frac {Q}{3E_{\mathrm {n}}I_{\mathrm {n}}}&=&\frac {3{\dot E}_{\mathrm {r}}\overline {\dot I}}{3E_{\mathrm {n}}I_{\mathrm {n}}} \\[ 5pt ]
\frac {P}{P_{\mathrm {n}}}+\mathrm {j}\frac {Q}{P_{\mathrm {n}}}&=&\frac {{\dot E}_{\mathrm {r}}}{E_{\mathrm {n}}}\frac {\overline {\dot I}}{I_{\mathrm {n}}} \\[ 5pt ]
P+\mathrm {j}Q &=&{\dot E}_{\mathrm {r}} \overline {\dot I} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となります。単位法で表す場合,\( \ 3 \ \)倍する必要がないことに注意して下さい。
3.電力円線図
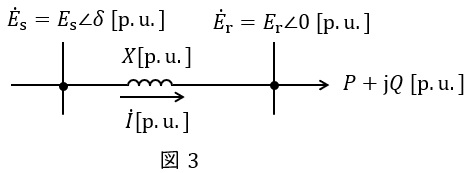
図3に示すような送電線路について電力円線図を考えます。図3において,送電端電圧\( \ {\dot E}_{\mathrm {s}}=E_{\mathrm {s}}∠\delta \ \mathrm {[p.u.]} \ \),受電端電圧\( \ {\dot E}_{\mathrm {r}}=E_{\mathrm {r}}∠0 \ \mathrm {[p.u.]} \ \),送電線を流れる電流\( \ \dot I \ \mathrm {[p.u.]} \ \),送電線のリアクタンス\( \ X \ \mathrm {[p.u.]} \ \)とし,送電線の抵抗分は無視できるとすると,ベクトル図は図4のようになります。ただし,\( \ \theta \ \mathrm {[rad]} \ \)は力率角です。ここで,送電線を流れる電流\( \ \dot I \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}&=&{\dot E}_{\mathrm {r}}+\mathrm {j}X\dot I \\[ 5pt ]
\end{eqnarray}
\]
の関係から,
\[
\begin{eqnarray}
\dot I&=&\frac {{\dot E}_{\mathrm {s}}-{\dot E}_{\mathrm {r}}}{\mathrm {j}X} \\[ 5pt ]
\end{eqnarray}
\]
となります。
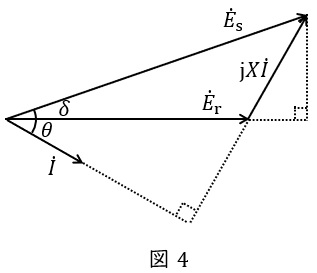
遅れ無効電力を正とすると,負荷への供給電力\( \ P+\mathrm {j}Q \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&{\dot E}_{\mathrm {r}} \overline {\dot I} \\[ 5pt ]
&=&{\dot E}_{\mathrm {r}}\cdot {\frac {\overline {{\dot E}_{\mathrm {s}}-{\dot E}_{\mathrm {r}}}}{\overline {\mathrm {j}X}}} \\[ 5pt ]
&=&E_{\mathrm {r}}\cdot \frac {E_{\mathrm {s}}\mathrm {e}^{-\mathrm {j}\delta }-E_{\mathrm {r}}}{-\mathrm {j}X} \\[ 5pt ]
&=&\mathrm {j}\frac {E_{\mathrm {s}}E_{\mathrm {r}}\mathrm {e}^{-\mathrm {j}\delta }-{E_{\mathrm {r}}}^{2}}{X} \\[ 5pt ]
&=&\mathrm {j}\frac {E_{\mathrm {s}}E_{\mathrm {r}}\left( \cos \delta -\mathrm {j}\sin \delta \right) -{E_{\mathrm {r}}}^{2}}{X} \\[ 5pt ]
&=&\frac {E_{\mathrm {s}}E_{\mathrm {r}}\sin \delta }{X}+\mathrm {j}\frac {E_{\mathrm {s}}E_{\mathrm {r}}\cos \delta -{E_{\mathrm {r}}}^{2}}{X} \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
P&=&\frac {E_{\mathrm {s}}E_{\mathrm {r}}\sin \delta }{X} \\[ 5pt ]
Q&=&\frac {E_{\mathrm {s}}E_{\mathrm {r}}\cos \delta -{E_{\mathrm {r}}}^{2}}{X} \\[ 5pt ]
\end{eqnarray}
\]
となります。上式を\( \ \sin \delta \ \)及び\( \ \cos \delta \ \)について整理すると,
\[
\begin{eqnarray}
\sin \delta &=&\frac {XP}{E_{\mathrm {s}}E_{\mathrm {r}}} \\[ 5pt ]
\cos \delta &=&\frac {XQ+{E_{\mathrm {r}}}^{2}}{E_{\mathrm {s}}E_{\mathrm {r}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \sin ^{2} \delta +\cos ^{2}\delta =1 \ \)の関係から,
\[
\begin{eqnarray}
\left( \frac {XP}{E_{\mathrm {s}}E_{\mathrm {r}}}\right) ^{2}+\left( \frac {XQ+{E_{\mathrm {r}}}^{2}}{E_{\mathrm {s}}E_{\mathrm {r}}}\right) ^{2} &=&1 \\[ 5pt ]
\left( XP\right) ^{2}+\left( XQ+{E_{\mathrm {r}}}^{2}\right) ^{2}&=&\left( E_{\mathrm {s}}E_{\mathrm {r}}\right) ^{2} \\[ 5pt ]
P^{2}+\left( Q+\frac {{E_{\mathrm {r}}}^{2}}{X}\right) ^{2}&=&\left( \frac {E_{\mathrm {s}}E_{\mathrm {r}}}{X}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
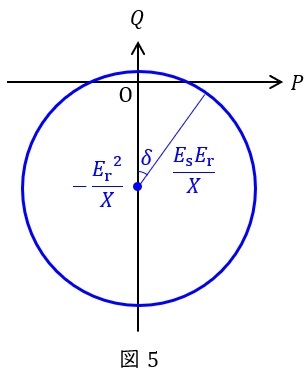
と整理でき,これにより図5に示すような中心が\( \ \displaystyle \left( 0, -\frac {{E_{\mathrm {r}}}^{2}}{X}\right) \ \)で半径\( \ \displaystyle \frac {E_{\mathrm {s}}E_{\mathrm {r}}}{X} \ \)の電力円線図を描くことができます。ただし,図5は\( \ E_{\mathrm {s}}>E_{\mathrm {r}} \ \)を前提としています。
【解答】
(1)a)送電端から流れ出す電流\( \ {\dot I}_{\mathrm {s}} \ \)
図1より,\( \ {\dot E}_{\mathrm {s}}={\dot E}_{\mathrm {r}}+\dot Z {\dot I}_{\mathrm {s}} \ \)であるから,これを\( \ {\dot I}_{\mathrm {s}} \ \)について整理すると,
\[
\begin{eqnarray}
\dot Z {\dot I}_{\mathrm {s}} &=&{\dot E}_{\mathrm {s}}-{\dot E}_{\mathrm {r}} \\[ 5pt ]
{\dot I}_{\mathrm {s}} &=&\frac {{\dot E}_{\mathrm {s}}-{\dot E}_{\mathrm {r}}}{\dot Z} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(1)b)送電端から流れ出す有効電力\( \ P_{\mathrm {s}} \ \),無効電力\( \ Q_{\mathrm {s}} \ \)
ワンポイント解説「3.電力円線図」と同様に計算していくと,
\[
\begin{eqnarray}
P_{\mathrm {s}}+\mathrm {j}Q_{\mathrm {s}}&=&{\dot E}_{\mathrm {s}}\overline {{\dot I}_{\mathrm {s}}} \\[ 5pt ]
&=&{\dot E}_{\mathrm {s}}\frac {\overline {{\dot E}_{\mathrm {s}}-{\dot E}_{\mathrm {r}}}}{\overline {\dot Z}} \\[ 5pt ]
&=&E_{\mathrm {s}}\mathrm {e}^{\mathrm {j}\delta }\frac {E_{\mathrm {s}}\mathrm {e}^{-\mathrm {j}\delta }-E_{\mathrm {r}}}{Z\mathrm {e}^{-\mathrm {j}\alpha }} \\[ 5pt ]
&=&\frac {{E_{\mathrm {s}}}^{2}-E_{\mathrm {s}}E_{\mathrm {r}}\mathrm {e}^{\mathrm {j}\delta }}{Z\mathrm {e}^{-\mathrm {j}\alpha }} \\[ 5pt ]
&=&\frac {{E_{\mathrm {s}}}^{2}}{Z}\mathrm {e}^{\mathrm {j}\alpha }-\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\mathrm {e}^{\mathrm {j}\left( \delta +\alpha \right) } \\[ 5pt ]
&=&\frac {{E_{\mathrm {s}}}^{2}}{Z}\left( \cos \alpha +\mathrm {j}\sin \alpha \right) -\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\left\{ \cos \left( \delta +\alpha \right) +\mathrm {j}\sin \left( \delta +\alpha \right) \right\} \\[ 5pt ]
&=&\frac {{E_{\mathrm {s}}}^{2}}{Z}\cos \alpha -\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\cos \left( \delta +\alpha \right) +\mathrm {j}\left\{ \frac {{E_{\mathrm {s}}}^{2}}{Z}\sin \alpha -\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\sin \left( \delta +\alpha \right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺の実部虚部を比較すると,
\[
\begin{eqnarray}
P_{\mathrm {s}}&=&\frac {{E_{\mathrm {s}}}^{2}}{Z}\cos \alpha -\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\cos \left( \delta +\alpha \right) \\[ 5pt ]
Q_{\mathrm {s}}&=&\frac {{E_{\mathrm {s}}}^{2}}{Z}\sin \alpha -\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\sin \left( \delta +\alpha \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(1)c)送電端円線図の中心\( \ \left( x_{\mathrm {1}},x_{\mathrm {2}}\right) \ \),半径\( \ x_{3} \ \)
(1)b)解答式を変形すると,
\[
\begin{eqnarray}
P_{\mathrm {s}}-\frac {{E_{\mathrm {s}}}^{2}}{Z}\cos \alpha &=&-\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\cos \left( \delta +\alpha \right) \\[ 5pt ]
Q_{\mathrm {s}}-\frac {{E_{\mathrm {s}}}^{2}}{Z}\sin \alpha &=&-\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\sin \left( \delta +\alpha \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺\( \ 2 \ \)乗すれば,
\[
\begin{eqnarray}
\left( P_{\mathrm {s}}-\frac {{E_{\mathrm {s}}}^{2}}{Z}\cos \alpha \right) ^{2}&=&\left( \frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\right) ^{2}\cos ^{2}\left( \delta +\alpha \right) \\[ 5pt ]
\left( Q_{\mathrm {s}}-\frac {{E_{\mathrm {s}}}^{2}}{Z}\sin \alpha \right) ^{2}&=&\left( \frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\right) ^{2}\sin ^{2}\left( \delta +\alpha \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,両式の両辺をそれぞれ加えると,
\[
\begin{eqnarray}
\left( P_{\mathrm {s}}-\frac {{E_{\mathrm {s}}}^{2}}{Z}\cos \alpha \right) ^{2}+\left( Q_{\mathrm {s}}-\frac {{E_{\mathrm {s}}}^{2}}{Z}\sin \alpha \right) ^{2}&=&\left( \frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\right) ^{2}\left\{ \cos ^{2}\left( \delta +\alpha \right) + \sin ^{2}\left( \delta +\alpha \right) \right\} \\[ 5pt ]
\left( P_{\mathrm {s}}-\frac {{E_{\mathrm {s}}}^{2}}{Z}\cos \alpha \right) ^{2}+\left( Q_{\mathrm {s}}-\frac {{E_{\mathrm {s}}}^{2}}{Z}\sin \alpha \right) ^{2}&=&\left( \frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,中心\( \ \displaystyle \left( x_{\mathrm {1}},x_{\mathrm {2}}\right) =\left( \frac {{E_{\mathrm {s}}}^{2}}{Z}\cos \alpha ,\frac {{E_{\mathrm {s}}}^{2}}{Z}\sin \alpha \right) \ \)及び半径\( \ \displaystyle x_{3}=\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z} \ \)と求められる。
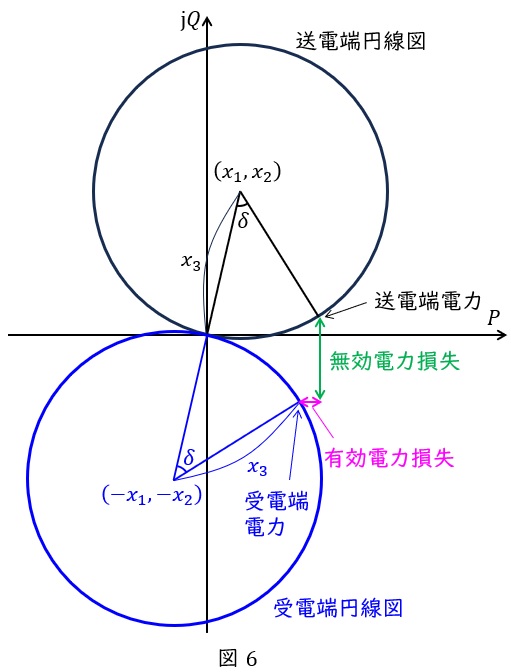
(2)受電端円線図を描き,有効電力損失,無効電力損失を図中に示す
(1)b)と同様に受電端での有効電力\( \ P_{\mathrm {r}} \ \)及び無効電力\( \ Q_{\mathrm {r}} \ \)とすると,\( \ {\dot I}_{\mathrm {s}}={\dot I}_{\mathrm {r}} \ \)であることに注意すれば
\[
\begin{eqnarray}
P_{\mathrm {r}}+\mathrm {j}Q_{\mathrm {r}}&=&{\dot E}_{\mathrm {r}}\overline {{\dot I}_{\mathrm {r}}} \\[ 5pt ]
&=&{\dot E}_{\mathrm {r}}\frac {\overline {{\dot E}_{\mathrm {s}}-{\dot E}_{\mathrm {r}}}}{\overline {\dot Z}} \\[ 5pt ]
&=&E_{\mathrm {r}}\frac {E_{\mathrm {s}}\mathrm {e}^{-\mathrm {j}\delta }-E_{\mathrm {r}}}{Z\mathrm {e}^{-\mathrm {j}\alpha }} \\[ 5pt ]
&=&\frac {E_{\mathrm {s}}E_{\mathrm {r}}\mathrm {e}^{-\mathrm {j}\delta }-{E_{\mathrm {r}}}^{2}}{Z\mathrm {e}^{-\mathrm {j}\alpha }} \\[ 5pt ]
&=&\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\mathrm {e}^{-\mathrm {j}\left( \delta -\alpha \right) }-\frac {{E_{\mathrm {r}}}^{2}}{Z}\mathrm {e}^{\mathrm {j}\alpha } \\[ 5pt ]
&=&\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\left\{ \cos \left( \delta -\alpha \right) -\mathrm {j}\sin \left( \delta -\alpha \right) \right\}-\frac {{E_{\mathrm {r}}}^{2}}{Z}\left( \cos \alpha +\mathrm {j}\sin \alpha \right) \\[ 5pt ]
&=&\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\cos \left( \delta -\alpha \right) -\frac {{E_{\mathrm {r}}}^{2}}{Z}\cos \alpha -\mathrm {j}\left\{ \frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\sin \left( \delta -\alpha \right) +\frac {{E_{\mathrm {r}}}^{2}}{Z}\sin \alpha \right\} \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺の実部虚部を比較すると,
\[
\begin{eqnarray}
P_{\mathrm {r}}&=&\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\cos \left( \delta -\alpha \right) -\frac {{E_{\mathrm {r}}}^{2}}{Z}\cos \alpha \\[ 5pt ]
Q_{\mathrm {r}}&=&-\left\{ \frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\sin \left( \delta -\alpha \right) +\frac {{E_{\mathrm {r}}}^{2}}{Z}\sin \alpha \right\} \\[ 5pt ]
\end{eqnarray}
\]
となる。(1)c)と同様に変形すると,
\[
\begin{eqnarray}
P_{\mathrm {r}}+\frac {{E_{\mathrm {r}}}^{2}}{Z}\cos \alpha &=&\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\cos \left( \delta -\alpha \right) \\[ 5pt ]
Q_{\mathrm {r}}+\frac {{E_{\mathrm {r}}}^{2}}{Z}\sin \alpha &=&-\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\sin \left( \delta -\alpha \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺\( \ 2 \ \)乗して加えると,
\[
\begin{eqnarray}
\left( P_{\mathrm {r}}+\frac {{E_{\mathrm {r}}}^{2}}{Z}\cos \alpha \right) ^{2}+\left( Q_{\mathrm {r}}+\frac {{E_{\mathrm {r}}}^{2}}{Z}\sin \alpha \right) ^{2}&=&\left( \frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\right) ^{2}\left\{ \cos ^{2}\left( \delta -\alpha \right) + \sin ^{2}\left( \delta -\alpha \right) \right\} \\[ 5pt ]
\left( P_{\mathrm {r}}+\frac {{E_{\mathrm {r}}}^{2}}{Z}\cos \alpha \right) ^{2}+\left( Q_{\mathrm {r}}+\frac {{E_{\mathrm {r}}}^{2}}{Z}\sin \alpha \right) ^{2}&=&\left( \frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z}\right) ^{2} \\[ 5pt ]
\left( P_{\mathrm {r}}+x_{1} \right) ^{2}+\left( Q_{\mathrm {r}}+x_{2} \right) ^{2}&=&{x_{3}}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,\( \ E_{\mathrm {s}}=E_{\mathrm {r}} \ \)に注意して,受電端円線図を描くと図6のようになり,位相差\( \ \delta \ \)での送電端及び受電端電力,有効電力損失及び無効電力損失は図6に示す通りとなる。
(3)送電端円線図の中心と半径を単位法で求める
送電線の抵抗\( \ R=5 \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X=20 \ \mathrm {[\Omega ]} \ \)を基準容量\( \ P_{\mathrm {n}}=1 \ 000 \ \mathrm {[MV\cdot A]} \ \),基準電圧\( \ E_{\mathrm {n}}=500 \ \mathrm {[kV]} \ \)の単位法に換算すると,
\[
\begin{eqnarray}
R \ \mathrm {[p.u.]}&=&\frac {RP_{\mathrm {n}}}{{E_{\mathrm {n}}}^{2}} \\[ 5pt ]
&=&\frac {5\times 1 \ 000\times 10^{6}}{\left( 500\times 10^{3}\right) ^{2}} \\[ 5pt ]
&=&0.02 \ \mathrm {[p.u.]} \\[ 5pt ]
X \ \mathrm {[p.u.]}&=&\frac {XP_{\mathrm {n}}}{{E_{\mathrm {n}}}^{2}} \\[ 5pt ]
&=&\frac {20\times 1 \ 000\times 10^{6}}{\left( 500\times 10^{3}\right) ^{2}} \\[ 5pt ]
&=&0.08 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であり,これより,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]}&=&\sqrt {R^{2}+X^{2}} \\[ 5pt ]
&=&\sqrt {0.02^{2}+0.08^{2}} \\[ 5pt ]
&≒&0.082 \ 462 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
\cos \alpha &=&\frac {R}{Z} \\[ 5pt ]
&=&\frac {0.02}{0.082 \ 462} \\[ 5pt ]
&≒&0.242 \ 54 \ \mathrm {[p.u.]} \\[ 5pt ]
\sin \alpha &=&\frac {X}{Z} \\[ 5pt ]
&=&\frac {0.08}{0.082 \ 462} \\[ 5pt ]
&≒&0.970 \ 14 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,(1)c)の通り送電端円線図の中心\( \ \left( x_{\mathrm {1}},x_{\mathrm {2}}\right) \ \),半径\( \ x_{3} \ \)は,
\[
\begin{eqnarray}
x_{\mathrm {1}} &=&\frac {{E_{\mathrm {s}}}^{2}}{Z}\cos \alpha \\[ 5pt ]
&=&\frac {1.0^{2}}{0.082 \ 462}\times 0.242 \ 54 \\[ 5pt ]
&≒&2.9412 → 2.94 \ \mathrm {[p.u.]} \\[ 5pt ]
x_{\mathrm {2}} &=&\frac {{E_{\mathrm {s}}}^{2}}{Z}\sin \alpha \\[ 5pt ]
&=&\frac {1.0^{2}}{0.082 \ 462}\times 0.970 \ 14 \\[ 5pt ]
&≒&11.765 → 11.8 \ \mathrm {[p.u.]} \\[ 5pt ]
x_{\mathrm {3}} &=&\frac {E_{\mathrm {s}}E_{\mathrm {r}}}{Z} \\[ 5pt ]
&=&\frac {1.0\times 1.0}{0.082 \ 462} \\[ 5pt ]
&≒&12.127 → 12.1 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
すなわち,送電端円線図の中心\( \ \left( x_{\mathrm {1}},x_{\mathrm {2}}\right) =\left( 2.94,11.8 \right) \ \),半径\( \ x_{3}=12.1 \ \),と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん