【問題】
【難易度】★★★★☆(やや難しい)
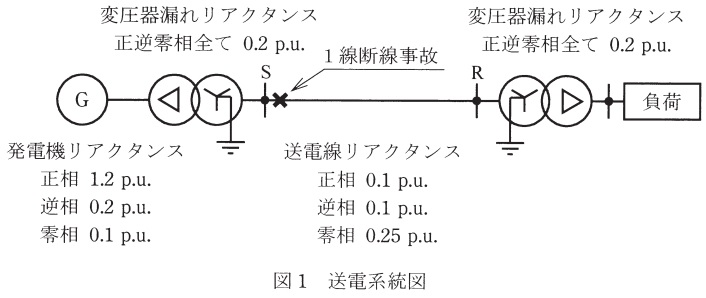
図1は1回線送電線を介して同期発電機,昇圧変圧器から三相平衡負荷へ送電している状況を示す。1線断線事故に関して,次の問に答えよ。ただし,送電線の作用静電容量は無視できるものとし,数値は全て\(100 \ \mathrm {MV\cdot A}\)基準の単位法で表現するものとする。
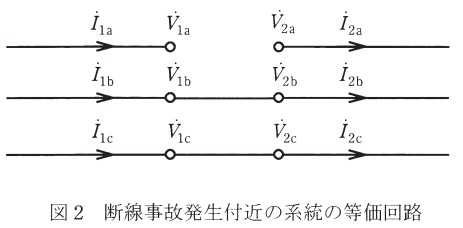
(1) 図1の送電線の送電端(昇圧変圧器高圧側母線\(\mathrm {S}\))近傍で1線断線が発生した回路の対称分等価回路を導出するために,図2のように元の系統を断線事故発生地点で二分割する。1線断線が発生したとき,図2の\({\dot I}_{\mathrm {1a}}\),\({\dot I}_{\mathrm {1b}}\),\({\dot I}_{\mathrm {1c}}\),\({\dot I}_{\mathrm {2a}}\),\({\dot I}_{\mathrm {2b}}\),\({\dot I}_{\mathrm {2c}}\),\({\dot V}_{\mathrm {1a}}\),\({\dot V}_{\mathrm {1b}}\),\({\dot V}_{\mathrm {1c}}\),\({\dot V}_{\mathrm {2a}}\),\({\dot V}_{\mathrm {2b}}\),\({\dot V}_{\mathrm {2c}}\)の間に成立する関係式(1線断線条件)を示せ。ただし,断線事故が発生した相を\(\mathrm {a}\)相とすること。
(2) 上記(1)で得られた関係式を対称座標変換すると1線断線条件が得られる。これを表現する図3の対称分等価回路の各\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に入るべき数値をそれぞれ答えよ。ただし,同じ文字をもつ\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)には同じ数値が入る。負荷を除く各回路要素のインピーダンスは全て\([\mathrm {p.u.}]\)で表現すること。
(3) 事故発生前の送電端(母線\(\mathrm {S}\))電圧を\(1.0 \ \mathrm {p.u.}\),ここからの送電電力を\(90 \ \mathrm {MW} +\mathrm {j} 10 \ \mathrm {Mvar}\)とする。以下の各問に答えよ。
a.事故発生前の発電機内部電圧(正相リアクタンス背後電圧)の大きさを計算せよ。
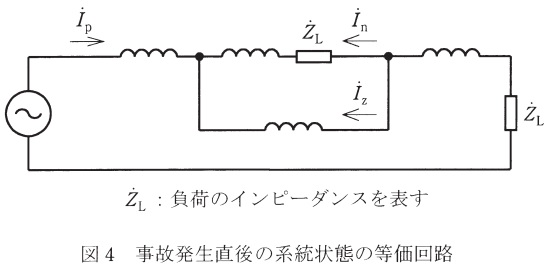
b.1線断線直後には発電機内部電圧(正相リアクタンス背後電圧)が変化しないものとして,事故発生直後の系統状態を図4で表現したときの電流\({\dot I}_{\mathrm {p}}\)を計算せよ。ただし,発電機内部電圧の位相を基準にすること。
c.1線断線直後の母線\(\mathrm {S}\)の事故相電圧の大きさを計算せよ。

【ワンポイント解説】
対称座標法による故障計算の問題です。対称座標法を用いた方法はパターン化されているため,慣れてしまうと取り組みやすい問題となりますが,計算がどうしても複雑になる傾向があるため,試験本番で選択するかどうかよく判断する必要があります。
1.対称座標法
故障計算をする際に,非常に便利な方法で,以下のように定義されます。
零相電圧\({\dot V}_{0}\),正相電圧\({\dot V}_{1}\),逆相電圧\({\dot V}_{2}\)とすると,各相の電圧\({\dot V}_{\mathrm {a}}\),\({\dot V}_{\mathrm {b}}\),\({\dot V}_{\mathrm {c}}\)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2}
\end{eqnarray}
\]
零相電流\({\dot I}_{0}\),正相電流\({\dot I}_{1}\),逆相電流\({\dot I}_{2}\)とすると,各相の電流\({\dot I}_{\mathrm {a}}\),\({\dot I}_{\mathrm {b}}\),\({\dot I}_{\mathrm {c}}\)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}
\end{eqnarray}
\]
また,対称座標法における発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-Z_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-Z_{2}{\dot I}_{2}
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)各電圧-電流間に成立する関係式(1線断線条件)
図2より各相の電圧及び電流に成立する関係式は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {1a}} &=&{\dot I}_{\mathrm {2a}}=0 \\[ 5pt ]
{\dot I}_{\mathrm {1b}} &=&{\dot I}_{\mathrm {2b}} \\[ 5pt ]
{\dot I}_{\mathrm {1c}} &=&{\dot I}_{\mathrm {2c}} \\[ 5pt ]
{\dot V}_{\mathrm {1b}} &=&{\dot V}_{\mathrm {2b}} \\[ 5pt ]
{\dot V}_{\mathrm {1c}} &=&{\dot V}_{\mathrm {2c}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)対称分等価回路の各\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に入るべき数値
題意で与えられた条件より,\(a~g\)に入る数値は,
\[
\begin{eqnarray}
a &=&\mathrm {j}1.2 \\[ 5pt ]
b &=&\mathrm {j}0.2 \\[ 5pt ]
c &=&\mathrm {j}0.1 \\[ 5pt ]
d &=&\mathrm {j}0.2 \\[ 5pt ]
e &=&\mathrm {j}0.1 \\[ 5pt ]
f &=&\mathrm {j}0.25 \\[ 5pt ]
g &=&\mathrm {j}0.2 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)a.事故発生前の発電機内部電圧(正相リアクタンス背後電圧)の大きさ
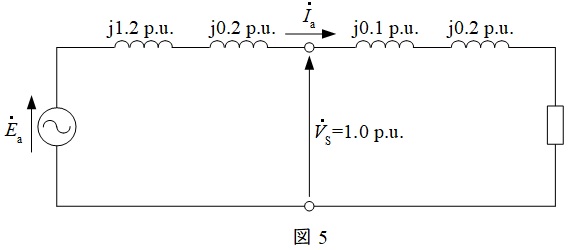
事故発生前の等価回路は図5のようになる。
送電電力\(P+\mathrm {j}Q\)から,\(100 \ \mathrm {MV\cdot A}\)基準の単位法で表すと,
\[
\begin{eqnarray}
P+\mathrm {j}Q &=&\frac {90}{100}+\mathrm {j}\frac {10}{100} \\[ 5pt ]
&=&0.9+\mathrm {j}0.1 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,事故発生前電流\({\dot I}_{\mathrm {a}}\)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&\frac {\overline {P+\mathrm {j}Q}}{\overline {{\dot V}_{\mathrm {s}}}} \\[ 5pt ]
&=&\frac {0.9-\mathrm {j}0.1}{1} \\[ 5pt ]
&=&0.9-\mathrm {j}0.1 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。以上と図3より発電機内部電圧\( \ {\dot E}_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {a}} &=&{\dot V}_{\mathrm {1p}}+\mathrm {j}X_{\mathrm {1p}}{\dot I}_{\mathrm {p}} \\[ 5pt ]
&=&1+\mathrm {j}1.4\times \left( 0.9-\mathrm {j}0.1 \right) \\[ 5pt ]
&=&1.14+\mathrm {j}1.26 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となりその大きさ\( \ E_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
\left| {\dot E}_{\mathrm {a}}\right| &=&\sqrt {1.14^{2}+1.26^{2}} \\[ 5pt ]
&=&1.6992 → 1.70 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)b.事故発生直後の正相電流\({\dot I}_{\mathrm {p}}\)
図5より,事故発生前の送電線からみた負荷側のインピーダンスは,負荷のインピーダンスを\(Z_{\mathrm {L}}\)とすると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s}} &=&\left( \mathrm {j}0.1 +\mathrm {j}0.2 +Z_{\mathrm {L}}\right) {\dot I}_{\mathrm {a}} \\[ 5pt ]
1 &=&\left( \mathrm {j}0.1 +\mathrm {j}0.2 +Z_{\mathrm {L}}\right) \times \left( 0.9-\mathrm {j}0.1 \right) \\[ 5pt ]
Z_{\mathrm {L}}&=&\frac {1}{0.9-\mathrm {j}0.1}-\mathrm {j}0.3 \\[ 5pt ]
&=&\frac {0.9+\mathrm {j}0.1}{0.81+0.01}-\mathrm {j}0.3 \\[ 5pt ]
&=&1.0976 -\mathrm {j}0.17805 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
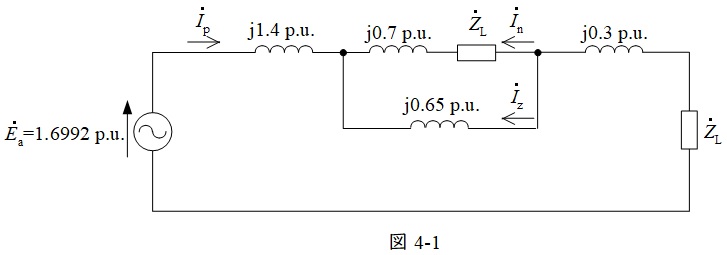
となる。よって,図4の等価回路の各値は図4-1のようになる。図4-1より,正相電流\({\dot I}_{\mathrm {p}}\)の大きさは,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {p}} &=&\frac {1.6992}{\mathrm {j}1.4+\mathrm {j}0.3+\frac {\mathrm {j}0.65\times \left( \mathrm {j}0.7+1.0976 -\mathrm {j}0.17805\right) }{\mathrm {j}0.65+ \left( \mathrm {j}0.7+1.0976 -\mathrm {j}0.17805\right) }+1.0976-\mathrm {j}0.17805} \\[ 5pt ]
&≒&\frac {1.6992}{1.0976+\mathrm {j}1.5220+\frac {-0.33927+\mathrm {j}0.71344 }{1.0976+\mathrm {j}1.1720 }} \\[ 5pt ]
&≒&\frac {1.6992}{1.0976+\mathrm {j}1.5220+\frac {-0.37238+\mathrm {j}0.78307+0.83615+\mathrm {j}0.39762 }{1.2047+1.3736 }} \\[ 5pt ]
&≒&\frac {1.6992}{1.2775+\mathrm {j}1.9799} \\[ 5pt ]
&≒&\frac {2.1707-\mathrm {j}3.3642}{1.6320+3.9200} \\[ 5pt ]
&≒&0.39098 -\mathrm {j}0.60594 → 0.391 -\mathrm {j}0.606\ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)c.1線断線直後の母線\(\mathrm {S}\)の事故相電圧の大きさ
図4-1より,逆相電流\({\dot I}_{\mathrm {n}}\)及び零相電流\({\dot I}_{\mathrm {z}}\)の大きさは,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {n}} &=&\frac {\mathrm {j}0.65}{\mathrm {j}0.65+ \left( \mathrm {j}0.7+1.0976 -\mathrm {j}0.17805\right) }\times \left( -{\dot I}_{\mathrm {p}}\right) \\[ 5pt ]
&=&\frac {\mathrm {j}0.65}{1.0976+\mathrm {j}1.1720 }\times \left\{ -\left( 0.39098 -\mathrm {j}0.60594\right) \right\} \\[ 5pt ]
&≒&\frac {-0.39386-\mathrm {j}0.25414}{2.5783}\times \left( 1.0976 -\mathrm {j}1.1720\right) \\[ 5pt ]
&≒&-0.28319+\mathrm {j}0.070845 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
{\dot I}_{\mathrm {z}} &=&\frac {\mathrm {j}0.7+1.0976 -\mathrm {j}0.17805}{\mathrm {j}0.65+ \left( \mathrm {j}0.7+1.0976 -\mathrm {j}0.17805\right) }\times \left( -{\dot I}_{\mathrm {p}}\right) \\[ 5pt ]
&=&\frac {\mathrm {j}0.7+1.0976 -\mathrm {j}0.17805}{1.0976+\mathrm {j}1.1720 }\times \left\{ -\left( 0.39098 -\mathrm {j}0.60594\right) \right\} \\[ 5pt ]
&≒&\frac {-0.74541+\mathrm {j}0.46101}{2.5783}\times \left( 1.0976 -\mathrm {j}1.1720\right) \\[ 5pt ]
&≒&-0.10777+\mathrm {j}0.53509 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。図3及びワンポイント解説「1.対称座標法」より,事故相電圧\({\dot V}_{\mathrm {1a}}\)の大きさは,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {1a}} &=&{\dot V}_{\mathrm {1p}}+{\dot V}_{\mathrm {1n}}+{\dot V}_{\mathrm {1z}} \\[ 5pt ]
&=&{\dot E}_{\mathrm {a}}-\mathrm {j}1.4{\dot I}_{\mathrm {p}}-\mathrm {j}0.4{\dot I}_{\mathrm {n}}-\mathrm {j}0.2{\dot I}_{\mathrm {z}} \\[ 5pt ]
&=&1.6992-\mathrm {j}1.4\times \left( 0.39098 -\mathrm {j}0.60594\right) -\mathrm {j}0.4\times \left( -0.28319+\mathrm {j}0.070845\right) -\mathrm {j}0.2\times \left( -0.10777+\mathrm {j}0.53509\right) \\[ 5pt ]
&≒&0.98624-\mathrm {j}0.41254 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\left| {\dot V}_{\mathrm {1a}}\right| &=&\sqrt {0.98624^{2}+0.41254^{2}} \\[ 5pt ]
&≒&1.0690 → 1.07 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん