【問題】
【難易度】★★★☆☆(普通)
距離リレーはその設置箇所の電圧,電流の測定値を用いて事故点までの距離を測定し,事故点が保護区間内にあるかどうかを判定している。図のような\( \ \mathrm {A} \ \)変電所に距離リレーを設置した系統を考える。送電線に二相短絡が発生した場合の距離リレーの動作について,次の問に答えよ。ただし,短絡のアーク抵抗と負荷電流は無視するものとし,\( \ \mathrm {b} \ \),\( \ \mathrm {c} \ \)相二相短絡事故発生時に図の距離リレーがみるインピーダンスは\( \ \displaystyle \frac {{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}}}{{\dot I}_{\mathrm {b1}}-{\dot I}_{\mathrm {c1}}} \ \)を二次側に換算した値であるものとする。また,各インピーダンスは正相,逆相共に同じであるとし,図の計算諸元は次のとおりとする。
・\( \ \mathrm {A} \ \)変電所母線の事故発生前の線間電圧\( \ 77 \ \mathrm {[kV]} \ \)
・\( \ \mathrm {A} \ \)変電所母線から電源側をみたインピーダンス\( \ {\dot Z}_{1}=\mathrm {j}0.5 \ \mathrm {[\Omega ]} \ \)
・各変電所間の送電線インピーダンス
\( \ {\dot Z}_{2}=\mathrm {j}3.5 \ \mathrm {[\Omega ]} \ \),\( \ {\dot Z}_{3}=\mathrm {j}2.0 \ \mathrm {[\Omega ]} \ \),\( \ {\dot Z}_{4}=\mathrm {j}1.0 \ \mathrm {[\Omega ]} \ \),\( \ {\dot Z}_{5}=\mathrm {j}4.0 \ \mathrm {[\Omega ]} \ \)
・\( \ \mathrm {A} \ \)変電所母線から事故点\( \ \mathrm {F_{1}} \ \),\( \ \mathrm {B} \ \)変電所母線から事故点\( \ \mathrm {F_{2}} \ \)までの送電線のインピーダンスをそれぞれ,\( \ {\dot Z}_{\mathrm {f1}}=\mathrm {j}3.0 \ \mathrm {[\Omega ]} \ \),\( \ {\dot Z}_{\mathrm {f2}}=\mathrm {j}2.5 \ \mathrm {[\Omega ]} \ \)
・\( \ \mathrm {CT}_{1} \ \)の\( \ \mathrm {CT} \ \)比 \( \ 600/5 \ \)
・送電線\( \ 1 \ \)を流れる\( \ \mathrm {b} \ \),\( \ \mathrm {c} \ \)相それぞれの電流(一次側) \( \ {\dot I}_{\mathrm {b1}} \ \),\( \ {\dot I}_{\mathrm {c1}} \ \)
・送電線\( \ 2 \ \)を流れる\( \ \mathrm {b} \ \),\( \ \mathrm {c} \ \)相それぞれの電流(一次側) \( \ {\dot I}_{\mathrm {b2}} \ \),\( \ {\dot I}_{\mathrm {c2}} \ \)
・\( \ \mathrm {VT}_{1} \ \)の\( \ \mathrm {VT} \ \)比 \( \ 77 \ 000/110 \ \)
・\( \ \mathrm {VT}_{1} \ \)における\( \ \mathrm {b} \ \),\( \ \mathrm {c} \ \)相それぞれの相電圧(一次側) \( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)
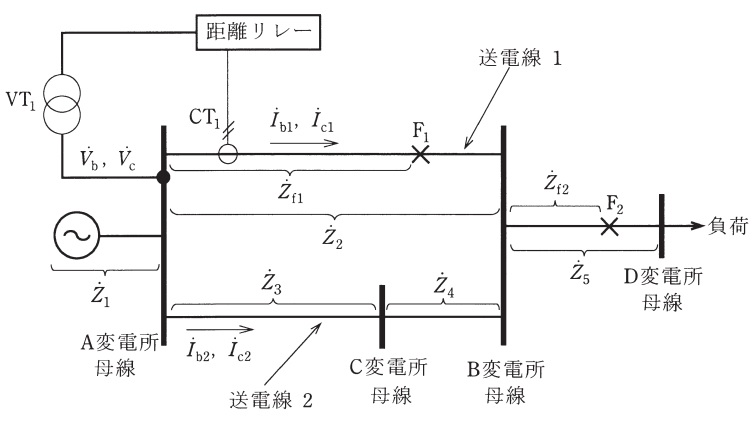
(1) 図の\( \ \mathrm {F_{1}} \ \)点において\( \ \mathrm {b} \ \),\( \ \mathrm {c} \ \)相二相短絡事故が発生したとする。事故発生中に距離リレーに入力される電圧\( \ {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} \ \)(一次側換算値)を\( \ {\dot I}_{\mathrm {b1}} \ \),\( \ {\dot Z}_{\mathrm {f1}} \ \)を用いて表し,距離リレーがみるインピーダンス(一次側換算値)を,\( \ {\dot Z}_{\mathrm {f1}} \ \)を用いて表せ。
(2) 図の\( \ \mathrm {F_{2}} \ \)点において\( \ \mathrm {b} \ \),\( \ \mathrm {c} \ \)相二相短絡事故が発生したとする。事故発生中に距離リレーに入力される電圧\( \ {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} \ \)(一次側換算値)を,\( \ {\dot I}_{\mathrm {b1}} \ \),\( \ {\dot I}_{\mathrm {b2}} \ \),\( \ {\dot Z}_{\mathrm {f2}} \ \),\( \ {\dot Z}_{\mathrm {2}} \ \)を用いて表し,距離リレーがみるインピーダンス(一次側換算値)を,\( \ {\dot Z}_{\mathrm {f2}} \ \)と\( \ {\dot Z}_{\mathrm {2}}~{\dot Z}_{\mathrm {4}} \ \)を用いて表せ。
(3) (2)の事故が発生したときに,距離リレーは動作域にあるかどうかを,根拠と共に示せ。ただし,距離リレーは\( \ \displaystyle \left| \frac {{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}}}{{\dot I}_{\mathrm {b1}}-{\dot I}_{\mathrm {c1}}} \right| \ \)を二次側換算した値を整定値とする仕様となっており,\( \ 5.0 \ \mathrm {[\Omega ]} \ \)以下で動作するものとする。
【ワンポイント解説】
対称座標法を用いた二相短絡事故に関する問題です。対称座標法を用いた計算問題はパターンがあり,この問題の場合,対称座標法の定義を理解しておくことと図1のような対称分等価回路の描き方を理解してしまえば比較的取り組みやすい問題となります。
1.対称座標法
故障計算をする際に,非常に便利な方法で,以下のように定義されます。
零相電圧\({\dot V}_{0}\),正相電圧\({\dot V}_{1}\),逆相電圧\({\dot V}_{2}\)とすると,各相の電圧\({\dot V}_{\mathrm {a}}\),\({\dot V}_{\mathrm {b}}\),\({\dot V}_{\mathrm {c}}\)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2}
\end{eqnarray}
\]
零相電流\({\dot I}_{0}\),正相電流\({\dot I}_{1}\),逆相電流\({\dot I}_{2}\)とすると,各相の電流\({\dot I}_{\mathrm {a}}\),\({\dot I}_{\mathrm {b}}\),\({\dot I}_{\mathrm {c}}\)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}
\end{eqnarray}
\]
また,対称座標法における発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-Z_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-Z_{2}{\dot I}_{2}
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)\( \ \mathrm {F_{1}} \ \)点にて二相短絡事故が発生した際に入力される電圧\( \ {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} \ \)(一次側換算値)及び距離リレーがみるインピーダンス(一次側換算値)
題意に沿って\( \ \mathrm {F_{1}} \ \)点にて二相短絡事故が発生した際の対称分等価回路は図1のようになる。二相短絡事故においては零相回路には電流は流れない。各電圧電流はそれぞれ図1の通りとする。
図1より,\( \ \mathrm {F_{1}} \ \)点の各電圧電流に関して,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {1f1}}&=&{\dot V}_{\mathrm {2f1}} & ・・・・・・・・・ ①& \\[ 5pt ]
{\dot I}_{\mathrm {1f1}}&=&-{\dot I}_{\mathrm {2f1}} & ・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかる。各インピーダンスが正相,逆相共に同じであることから,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {11}}&=&-{\dot I}_{\mathrm {21}} & ・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となる。
ワンポイント解説「1.対称座標法」より,距離リレーにかかる電圧\( \ {\dot V}_{\mathrm {b}} \ \)及び\( \ {\dot V}_{\mathrm {c}} \ \)は,零相電圧が零であるので,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {b}} &=& a^{2}{\dot V}_{1} + a{\dot V}_{2} & ・・・・・・・・・ ④& \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=& a{\dot V}_{1} + a^{2}{\dot V}_{2} & ・・・・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} &=& \left( a^{2}-a\right) \left( {\dot V}_{1} – {\dot V}_{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,図1より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {1}}&=&{\dot V}_{\mathrm {1f1}}+{\dot Z}_{\mathrm {f1}}{\dot I}_{\mathrm {11}} \\[ 5pt ]
{\dot V}_{\mathrm {2}}&=&{\dot V}_{\mathrm {2f1}}+{\dot Z}_{\mathrm {f1}}{\dot I}_{\mathrm {21}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを代入すると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} &=& \left( a^{2}-a\right) \left( {\dot V}_{\mathrm {1f1}}+{\dot Z}_{\mathrm {f1}}{\dot I}_{\mathrm {11}} – {\dot V}_{\mathrm {2f1}}-{\dot Z}_{\mathrm {f1}}{\dot I}_{\mathrm {21}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,①及び③の関係を用いると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} &=& \left( a^{2}-a\right) \left( {\dot V}_{\mathrm {1f1}}+{\dot Z}_{\mathrm {f1}}{\dot I}_{\mathrm {11}} – {\dot V}_{\mathrm {1f1}}+{\dot Z}_{\mathrm {f1}}{\dot I}_{\mathrm {11}}\right) \\[ 5pt ]
&=& 2\left( a^{2}-a\right){\dot Z}_{\mathrm {f1}}{\dot I}_{\mathrm {11}} \\[ 5pt ]
\end{eqnarray}
\]
となる。距離リレーの電流\( \ {\dot I}_{\mathrm {b1}} \ \)及び\( \ {\dot I}_{\mathrm {c1}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {b1}} &=&a^{2}{\dot I}_{11} + a{\dot I}_{21}&=&\left( a^{2}-a\right) {\dot I}_{11} & ・・・・・・・・・ ⑥& \\[ 5pt ]
{\dot I}_{\mathrm {c1}} &=&a{\dot I}_{11} + a^{2}{\dot I}_{21}&=&-\left( a^{2}-a\right) {\dot I}_{11} & ・・・・・・・・・ ⑦& \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} &=& 2{\dot Z}_{\mathrm {f1}}{\dot I}_{\mathrm {b1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,距離リレーが見るインピーダンス\( \ {\dot Z}_{\mathrm {R}} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}} &=& \frac {{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}}}{{\dot I}_{\mathrm {b1}}-{\dot I}_{\mathrm {c1}}} \\[ 5pt ]
&=& \frac {2{\dot Z}_{\mathrm {f1}}{\dot I}_{\mathrm {b1}}}{2{\dot I}_{\mathrm {b1}}} \\[ 5pt ]
&=& {\dot Z}_{\mathrm {f1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
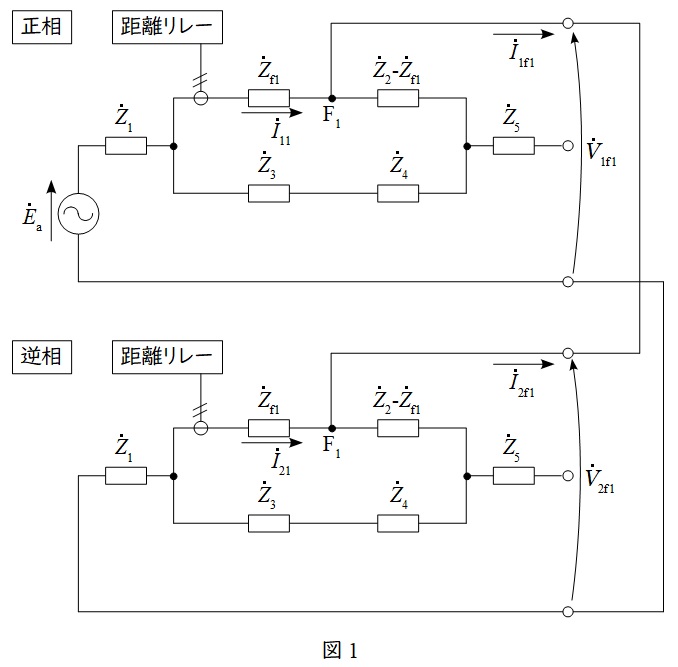
(2)\( \ \mathrm {F_{2}} \ \)点にて二相短絡事故が発生した際に入力される電圧\( \ {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} \ \)(一次側換算値)及び距離リレーがみるインピーダンス(一次側換算値)
題意に沿って\( \ \mathrm {F_{2}} \ \)点にて二相短絡事故が発生した際の対称分等価回路は図2のようになる。各電圧電流はそれぞれ図2の通りとする。
図2より,\( \ \mathrm {F_{2}} \ \)点の各電圧電流に関する関係式は(1)と同様となる。すなわち,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {1f2}}&=&{\dot V}_{\mathrm {2f2}} & ・・・・・・・・・ ①^{\prime }& \\[ 5pt ]
{\dot I}_{\mathrm {1f2}}&=&-{\dot I}_{\mathrm {2f2}} & ・・・・・・・・・ ②^{\prime }& \\[ 5pt ]
{\dot I}_{\mathrm {11}}&=&-{\dot I}_{\mathrm {21}} & ・・・・・・・・・ ③^{\prime }& \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=& a^{2}{\dot V}_{1} + a{\dot V}_{2} & ・・・・・・・・・ ④^{\prime }& \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=& a{\dot V}_{1} + a^{2}{\dot V}_{2} & ・・・・・・・・・ ⑤^{\prime }& \\[ 5pt ]
{\dot I}_{\mathrm {b1}}&=&\left( a^{2}-a\right) {\dot I}_{11} & ・・・・・・・・・ ⑥^{\prime }& \\[ 5pt ]
{\dot I}_{\mathrm {c1}}&=&-\left( a^{2}-a\right) {\dot I}_{11} & ・・・・・・・・・ ⑦^{\prime }& \\[ 5pt ]
\end{eqnarray}
\]
となる。また,図2の等価回路より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {1}}&=&{\dot V}_{\mathrm {1f2}}+{\dot Z}_{\mathrm {2}}{\dot I}_{\mathrm {11}}+{\dot Z}_{\mathrm {f2}}{\dot I}_{\mathrm {1f2}} & ・・・・・・・・・ ⑧& \\[ 5pt ]
{\dot V}_{\mathrm {2}}&=&{\dot V}_{\mathrm {2f2}}+{\dot Z}_{\mathrm {2}}{\dot I}_{\mathrm {21}}+{\dot Z}_{\mathrm {f2}}{\dot I}_{\mathrm {2f2}} & ・・・・・・・・・ ⑨& \\[ 5pt ]
\end{eqnarray}
\]
となる。\(④^{\prime }\),\(⑤^{\prime }\),⑧,⑨の関係式より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}} &=& \left( a^{2}-a\right) \left( {\dot V}_{1}- {\dot V}_{2}\right) \\[ 5pt ]
&=& \left( a^{2}-a\right) \left( {\dot V}_{\mathrm {1f2}}+{\dot Z}_{\mathrm {2}}{\dot I}_{\mathrm {11}}+{\dot Z}_{\mathrm {f2}}{\dot I}_{\mathrm {1f2}}- {\dot V}_{\mathrm {2f2}}-{\dot Z}_{\mathrm {2}}{\dot I}_{\mathrm {21}}-{\dot Z}_{\mathrm {f2}}{\dot I}_{\mathrm {2f2}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,\(①^{\prime }\),\(②^{\prime }\),\(③^{\prime }\)の関係式より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}}&=& \left( a^{2}-a\right) \left( 2{\dot Z}_{\mathrm {2}}{\dot I}_{\mathrm {11}}+2{\dot Z}_{\mathrm {f2}}{\dot I}_{\mathrm {1f2}}\right) \\[ 5pt ]
\end{eqnarray}
\]
と整理され,さらに分流の法則により,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {11}}&=& \frac {{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}}{{\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}}{\dot I}_{\mathrm {1f2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}}&=& 2\left( a^{2}-a\right) \left( {\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {f2}}\frac {{\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}}{{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}}\right) {\dot I}_{\mathrm {11}} \\[ 5pt ]
\end{eqnarray}
\]
となり,さらに\(⑥^{\prime }\)の関係式より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}}&=& 2 \left( {\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {f2}}\frac {{\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}}{{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}}\right) {\dot I}_{\mathrm {b1}} \\[ 5pt ]
&=& 2 \left( {\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {f2}}\right) {\dot I}_{\mathrm {b1}}+2{\dot Z}_{\mathrm {f2}}\frac {{\dot Z}_{\mathrm {2}}}{{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}}{\dot I}_{\mathrm {b1}} \\[ 5pt ]
&=& 2 \left\{ \left( {\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {f2}}\right) {\dot I}_{\mathrm {b1}}+{\dot Z}_{\mathrm {f2}}{\dot I}_{\mathrm {b2}}\right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,距離リレーが見るインピーダンス\( \ {\dot Z}_{\mathrm {R}} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}} &=& \frac {{\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {c}}}{{\dot I}_{\mathrm {b1}}-{\dot I}_{\mathrm {c1}}} \\[ 5pt ]
&=& \frac {\displaystyle 2 \left( {\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {f2}}\frac {{\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}}{{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}}\right) {\dot I}_{\mathrm {b1}}}{2{\dot I}_{\mathrm {b1}}} \\[ 5pt ]
&=& {\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {f2}}\frac {{\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}}{{\dot Z}_{\mathrm {3}}+{\dot Z}_{\mathrm {4}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)(2)の事故が発生したときに,距離リレーは動作域にあるかどうか
(2)の解答式に各値を代入すると,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=& \mathrm {j}3.5+\mathrm {j}2.5\times \frac {\mathrm {j}3.5+\mathrm {j}2.0+\mathrm {j}1.0}{\mathrm {j}2.0+\mathrm {j}1.0} \\[ 5pt ]
&≒& \mathrm {j}8.9167 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となり,二次側に換算すると,
\[
\begin{eqnarray}
\mathrm {j}8.9167\times \frac {110}{77000}\times \frac {600}{5}&≒& \mathrm {j}1.5286 → 1.53 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,整定値\( \ 5.0 \ \mathrm {[\Omega ]} \ \)以下なので動作域にある。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん