《電力・管理》〈送電〉[R06:問3]地中送電線路の電力用ケーブルの送電特性に関する論説問題

【問題】

【難易度】★★★★☆（やや難しい）

地中送電線路の電力用ケーブルの送電特性について，次の問に答えよ。

(1)　電力用ケーブルにおける抵抗損以外の電力損失について\( \ 2 \ \)点あげ，その電力損失が大きくなり留意が必要となる状況と理由について各々\( \ 50 \ \)字程度以内で述べよ。

(2)　許容送電電力\( \ \mathrm {[MV\cdot A]} \ \)が決まる要因及び増大させる方策について\( \ 200 \ \)字程度以内で述べよ。

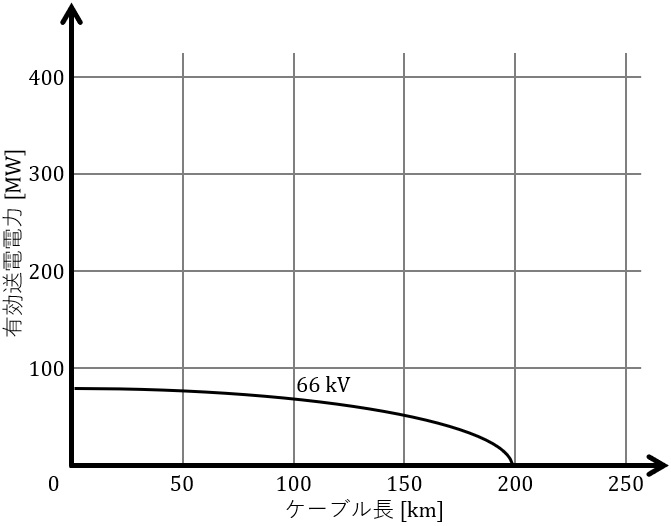
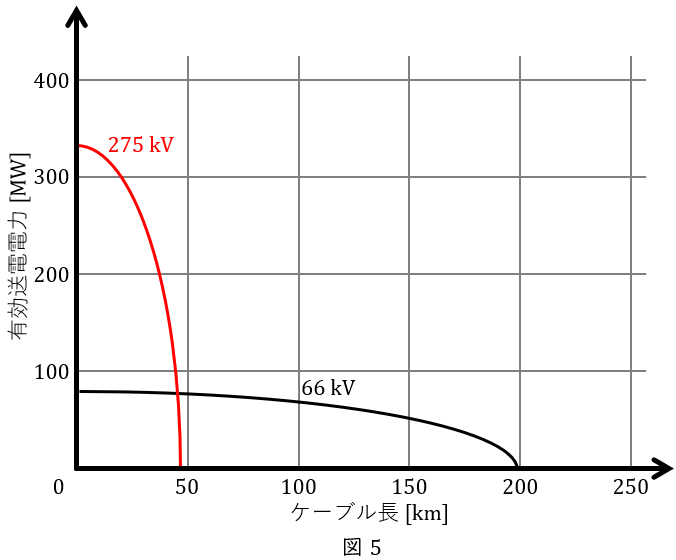
(3)　有効送電電力\( \ \mathrm {[MW]} \ \)と限界のケーブル長の相関性について電圧が高くなるとどうなるか理由を含め\( \ 50 \ \)字程度以内で述べよ。また，図の線間電圧\( \ V \ \)が\( \ 66 \ \mathrm {kV} \ \)のケーブル長と有効送電電力の関係を踏まえて，答案用紙に印刷されている図中に\( \ V \ \)が\( \ 275 \ \mathrm {kV} \ \)の線路の特性を概略で記載せよ。なお，どちらも許容送電電流\( \ I=700 \ \mathrm {A} \ \)，静電容量\( \ C=0.3 \ \mathrm {\mu F/km} \ \)，周波数\( \ f=50 \ \mathrm {Hz} \ \)として，単位長当たりの充電電流\( \ \displaystyle I_{\mathrm {C}}=\frac {2}{\sqrt {3}}\pi f CV \ \mathrm {[A]} \ \)とする。

【ワンポイント解説】

ケーブルの損失と許容送電電力に関する問題です。
ケーブルの損失は許容電力と関連性も深く検討する上で重要な内容ですが，(3)の内容はあまり電験では出題されたのを見たことがないので，受験生には少し厳しい問題であったかなと思います。

1.ケーブルに発生する損失
①抵抗損
導体部の抵抗により発生する損失で，導体電流の\( \ 2 \ \)乗に比例します。

②誘電体損
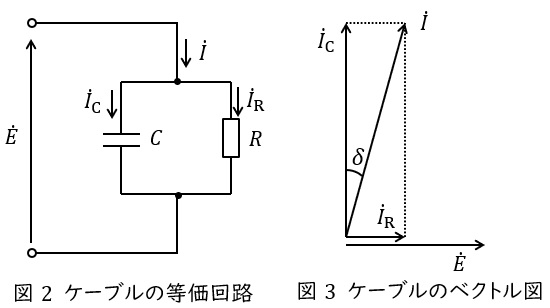
ケーブルの絶縁体部に流れる電流のうち，抵抗成分に流れる電流による損失です。ケーブルは誘電体を金属で挟んだコンデンサのような構造をしているため，損失分も合わせ一相分等価回路は図2のように抵抗\( \ R \ \mathrm {[\Omega ]} \ \)と静電容量\( \ C \ \mathrm {[F]} \ \)の並列回路となり，図3のベクトル図に示すような電流が流れます。ただし，\( \ \dot E \ \mathrm {[V]} \ \)はケーブルに加わる電圧の相電圧となります。
この時のコンデンサ分に流れる電流\( \ I_{\mathrm {C}} \ \mathrm {[A]} \ \)に対する抵抗分に流れる電流\( \ I_{\mathrm {R}} \ \mathrm {[A]} \ \)の割合\( \ \displaystyle \frac {I_{\mathrm {R}}}{I_{\mathrm {C}}}=\tan \delta \ \)を誘電正接と呼び，ケーブルが劣化してくると大きくなります。
ケーブルの誘電体損\( \ W_{\mathrm {d}} \ \mathrm {[W]} \ \)は，ケーブルに加わる電圧（線間電圧）を\( \ V \ \mathrm {[V]} \ \)，周波数を\( \ f \ \mathrm {[Hz]} \ \)，角周波数を\( \ \omega =2\pi f \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
W_{\mathrm {d}}&=&3\frac {V}{\sqrt {3}}I_{\mathrm {R}} \\[ 5pt ] &=&3\frac {V}{\sqrt {3}}I_{\mathrm {C}}\tan \delta \\[ 5pt ] &=&3\frac {V}{\sqrt {3}}\left( \omega C\frac {V}{\sqrt {3}}\right) \tan \delta \\[ 5pt ] &=&\omega CV^{2}\tan \delta \\[ 5pt ] &=&2\pi f CV^{2}\tan \delta \\[ 5pt ] \end{eqnarray}
\] となり，誘電体損は電圧\( \ V \ \mathrm {[V]} \ \)の\( \ 2 \ \)乗に比例し，周波数\( \ f \ \mathrm {[Hz]} \ \)，誘電正接\( \ \tan \delta \ \)に比例することがわかります。

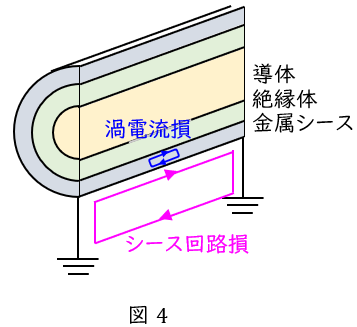
③シース損
ケーブルの絶縁体部の外側に巻く金属（シース）に発生する損失で，図4に示すようにシースを流れる循環電流によるシース回路損と渦電流による渦電流損があります。ケーブル導体を流れる電流から発生する磁束により電圧が誘起され損失が発生します。

2.許容電流の種類
電線の断面積を選定する際に検討する許容電流には大きく分けて以下の\( \ 3 \ \)種類があります。

①常時許容電流
　常時供給する負荷の容量もしくは将来の増設を見越し，連続して使用しても電線に問題の発生しない電流値の限度を考慮するものです。

②短時間許容電流
　送電の系統切換え時に一時的に流れる電流，並行\( \ 2 \ \)回線の送電線で\( \ 1 \ \)回線で事故が発生し停止した際に健全な送電線に流れる電流，隣接の電線で事故が発生した際に健全な電線路から電力を融通する場合において健全な電線路に流れる電流，等の数分～数時間程度流れても電線に問題が発生しない電流値の限度をいいます。

③瞬時許容電流
　短絡事故等の事故時に発生する数秒程度の大きな電流において，許容できる電流値のことをいいます。

3.地中送電の送電容量上昇対策
地中送電は架空送電と比較して放熱性が低いため，一般に導体の太さが同じ場合，送電容量が小さくなります。したがって，以下に示すような送電容量上昇対策を行うことがあります。

①熱損失抑制
　導体サイズを大きくする，誘電正接の小さい絶縁材料を使用する，等により発生する熱損失自体を小さくします。

②強制冷却
　ケーブルに直接冷却媒体を循環させる内部冷却，及び外部冷却としてケーブルの管路に冷却水を通水する直接冷却，ケーブルの管路と並行して布設した冷却水の管路に通水する間接冷却があります。

③耐熱性の高い絶縁材料の使用
　許容温度が比較的高い絶縁材料を使用します。

【解答】

(1)ケーブルにおける抵抗損以外の電力損失\( \ 2 \ \)点とその電力損失が大きくなり留意が必要となる状況と理由
(ポイント)
・ワンポイント解説「1.ケーブルに発生する損失」の通りです。
・シース内に三相導体が収納されている三心ケーブルに比べ，単心ケーブルではシース電圧が大きくなる傾向にあります。

(試験センター解答)
誘電体損：超高圧以上では，誘電体損が電圧の\( \ 2 \ \)乗に比例して大きくなるため，問題となる。
シース損：三相回路に単相ケーブルを用いると，それぞれに大きなシース損が発生し，三条合わせて用いるとさらに大きくなるため，問題となる。

(2)許容送電電力\( \ \mathrm {[MV\cdot A]} \ \)が決まる要因及び増大させる方策
(ポイント)
・ワンポイント解説「2.許容電流の種類」及び「3.地中送電の送電容量上昇対策」の通りです。
・ケーブルの送電電力は最終的に絶縁体の許容温度で決まり，その対策を定性的に説明すれば高得点が得られるかと思います。

(試験センター解答)
電力用ケーブルは，熱的限界からくる許容電流以上に電流を流せないことから，許容送電電力は許容電流によって決まる。許容電流は絶縁体に影響を及ぼさない導体の最高許容温度によって決められ，常時許容電流，短時間許容電流，瞬時許容電流等を考慮して決められる。許容送電電力を増大させる方策は，許容電流を増やすために導体を太くする，条数を増やす，強制冷却（内部冷却，外部冷却，間接冷却）する方法がある。

(3)有効送電電力\( \ \mathrm {[MW]} \ \)と限界のケーブル長の相関性について電圧が高くなるとどうなるか，また図中に\( \ V \ \)が\( \ 275 \ \mathrm {kV} \ \)の線路の特性を概略で記載
(ポイント)
・論述問題の回答は本番の試験では，有効送電電力とケーブル長の関係を式にして最後に記載すると良いかと思います。

(試験センター解答)
ある有効送電電力を送ることができる限界のケーブル長（臨界ケーブル長）が存在し，電圧が高くなるにつれて著しく短くなる。

題意より，\( \ V_{1}=66 \ \mathrm {[kV]} \ \)及び\( \ V_{2}=275 \ \mathrm {[kV]} \ \)のときの単位長当たりの充電電流\( \ I_{\mathrm {C1}} \ \mathrm {[A]} \ \)及び\( \ I_{\mathrm {C2}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {C1}}&=&\frac {2}{\sqrt {3}}\pi f CV_{1} \\[ 5pt ] &=&\frac {2}{\sqrt {3}}\pi \times 50 \times 0.3\times 10^{-6}\times 66 \times 10^{3} \\[ 5pt ] &≒&3.5913 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {C2}}&=&\frac {2}{\sqrt {3}}\pi f CV_{2} \\[ 5pt ] &=&\frac {2}{\sqrt {3}}\pi \times 50 \times 0.3\times 10^{-6}\times 275 \times 10^{3} \\[ 5pt ] &≒&14.964 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] なので，それぞれの無効電力\( \ Q_{1} \ \mathrm {[Mvar]} \ \)及び\( \ Q_{2} \ \mathrm {[Mvar]} \ \)は，
\[
\begin{eqnarray}
Q_{1}&=&3\times \frac {V_{1}}{\sqrt {3}}I_{\mathrm {C1}}L \\[ 5pt ] &=&3\times \frac {66 \times 10^{3}}{\sqrt {3}}\times 3.5913L \\[ 5pt ] &≒&410 \ 540L \ \mathrm {[var]}　→　0.410 \ 54L \ \mathrm {[Mvar]} \\[ 5pt ] Q_{2}&=&3\times \frac {V_{2}}{\sqrt {3}}I_{\mathrm {C2}}L \\[ 5pt ] &=&3\times \frac {275 \times 10^{3}}{\sqrt {3}}\times 14.964L \\[ 5pt ] &≒&7 \ 127 \ 600L \ \mathrm {[var]}　→　7.127 \ 6L \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
\] となる。一方，許容皮相電力\( \ S_{1} \ \mathrm {[MV\cdot A]} \ \)及び\( \ S_{2} \ \mathrm {[MV\cdot A]} \ \)は，
\[
\begin{eqnarray}
S_{1}&=&3\times \frac {V_{1}}{\sqrt {3}}I \\[ 5pt ] &=&3\times \frac {66 \times 10^{3}}{\sqrt {3}}\times 700 \\[ 5pt ] &≒&80 \ 021 \ 000 \ \mathrm {[V\cdot A]}　→　80.021 \ \mathrm {[MV\cdot A]} \\[ 5pt ] S_{2}&=&3\times \frac {V_{2}}{\sqrt {3}}I \\[ 5pt ] &=&3\times \frac {275 \times 10^{3}}{\sqrt {3}}\times 700 \\[ 5pt ] &≒&333 \ 420 \ 000 \ \mathrm {[V\cdot A]}　→　333.42 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，有効送電電力\( \ P_{1} \ \mathrm {[MW]} \ \)及び\( \ P_{2} \ \mathrm {[MW]} \ \)と無効電力\( \ Q_{1} \ \mathrm {[Mvar]} \ \)及び\( \ Q_{2} \ \mathrm {[Mvar]} \ \)の関係は，三平方の定理より，
\[
\begin{eqnarray}
P_{1}^{2}+Q_{1}^{2}&=&S_{1}^{2} \\[ 5pt ] P_{1}^{2}+\left( 0.410 \ 54L\right) ^{2}&=&80.021^{2} \\[ 5pt ] P_{2}^{2}+Q_{2}^{2}&=&S_{2}^{2} \\[ 5pt ] P_{2}^{2}+\left( 7.127 \ 6L\right) ^{2}&=&333.42^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。これより，線路の特性は原点を中心とする楕円形を描くことがわかり，\( \ P_{1}=0 \ \)及び\( \ P_{2}=0 \ \)のとき，
\[
\begin{eqnarray}
\left( 0.410 \ 54L\right) ^{2}&=&80.021^{2} \\[ 5pt ] 0.410 \ 54L&=&80.021 \\[ 5pt ] L&≒&194.92 \ \mathrm {[km]} \\[ 5pt ] \left( 7.127 \ 6L\right) ^{2}&=&333.42^{2} \\[ 5pt ] 7.127 \ 6L&=&333.42 \\[ 5pt ] L&≒&46.783 \ \mathrm {[km]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ L=0 \ \)のとき，
\[
\begin{eqnarray}
P_{1}^{2}&=&80.021^{2}\\[ 5pt ] P_{1}&=&80.021 \ \mathrm {[MW]} \\[ 5pt ] P_{2}^{2}&=&333.42^{2} \\[ 5pt ] P_{2}&=&333.42 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}
\] となるので，特性図は図5のようになる。