【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,電力系統の潮流計算に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
電力系統の構成を,変圧器や送電線などの電力輸送設備を表す「ブランチ」と,発電機や負荷端子などの母線を表す「ノード」の組み合わせにより表すことを考える。
図の電力系統において,全ての変数は共通の基準値による単位法表現とする。ノード\( \ i\left( i=1,2,3\right) \ \)の電圧を\( \ {\dot V}_{i} \ \),ノード\( \ i – j\left( j=1,2,3\right) \ \)間のブランチのアドミタンスを\( \ {\dot y}_{ij}=g_{ij}-\mathrm {j}b_{ij} \ \)とし,ブランチの対地アドミタンスは無視できる場合,ノード\( \ i \ \)に注入される電流\( \ {\dot I}_{i} \ \)は次式で表される。
\[
\begin{eqnarray}
\begin{bmatrix}
{\dot I}_{1} \\
{\dot I}_{2} \\
{\dot I}_{3} \\
\end{bmatrix} &=& \dot Y\begin{bmatrix}
{\dot V}_{1} \\
{\dot V}_{2} \\
{\dot V}_{3} \\
\end{bmatrix} \left( \dot Y=\begin{bmatrix}
{\dot Y}_{11} & {\dot Y}_{12} & {\dot Y}_{13} \\
{\dot Y}_{21} & {\dot Y}_{22} & {\dot Y}_{23} \\
{\dot Y}_{31} & {\dot Y}_{32} & {\dot Y}_{33} \\
\end{bmatrix}\right) \\[ 5pt ]
\end{eqnarray}
\]
ここで,アドミタンス行列\( \ \dot Y \ \)は\( \ {\dot y}_{ij} \ \)を用いると\( \ \fbox { (1) } \ \)により表される。
また,ノード\( \ i- j \ \)間の電圧の位相差\( \ \delta _{ij} \ \)を\( \ \delta _{ij}=\delta _{i}-\delta _{j} \ \),アドミタンス\( \ {\dot Y}_{ij}=Y_{ij}∠\theta _{ij} \ \)を\( \ \dot Y \ \)の\( \ i \ \)行目\( \ j \ \)列目の成分とすると,ノード\( \ i \ \)に注入される有効電力\( \ P _{i} \ \)と無効電力\( \ Q _{i} \ \)は,遅れの無効電力を正と定義すると\( \ \fbox { (2) } \ \)と定式化でき,これを電力方程式と呼ぶ。ブランチの抵抗成分を無視できる場合,\( \ \theta _{12} =\theta _{23} =\fbox { (3) } \ \)となる。さらに,\( \ \sin \delta _{12}= \delta _{12} \ \),\( \ \sin \delta _{23}= \delta _{23} \ \),\( \ V_{1}=V_{2}=V_{3}=1.0 \ \)の近似がそれぞれ成立する場合,\( \ P_{2} \ \)の近似式は\( \ \fbox { (4) } \ \)と表すことができる。
ノードの種別に応じた拘束条件の下で電力方程式を解くことを,一般に潮流計算と呼ぶ。\( \ \fbox { (5) } \ \)機能を有する発電機が接続するノードでは,有効電力出力並びに\( \ \fbox { (6) } \ \)の目標値を拘束条件として与える。負荷の接続するノードでは,負荷の有効電力と無効電力が拘束条件となる。また,スラックノードは解析対象の電力系統全体での\( \ \fbox { (7) } \ \)を補償する役割を担う。
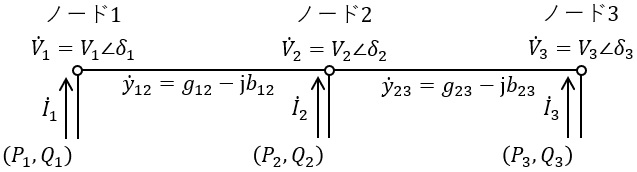
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \begin{bmatrix}
{\dot y}_{12} & -{\dot y}_{12} & 0 \\
-{\dot y}_{12} & {\dot y}_{12}+{\dot y}_{23} & -{\dot y}_{23} \\
0 & -{\dot y}_{23} & {\dot y}_{23} \\
\end{bmatrix} &(ロ)& \begin{bmatrix}
-{\dot y}_{12} & {\dot y}_{12} & 0 \\
{\dot y}_{12} & -{\dot y}_{12}-{\dot y}_{23} & {\dot y}_{23} \\
0 & {\dot y}_{23} & -{\dot y}_{23} \\
\end{bmatrix} \\[ 5pt ]
&(ハ)& \begin{bmatrix}
{\dot y}_{12} & {\dot y}_{12} & 0 \\
{\dot y}_{12} & {\dot y}_{12}+{\dot y}_{23} & {\dot y}_{23} \\
0 & {\dot y}_{23} & {\dot y}_{23} \\
\end{bmatrix} &(ニ)& \left\{
\begin{array}{l}
P_{i} = \displaystyle \sum_{j=1}^{3} Y_{ij}V_{i}V_{j}\sin \left( \delta _{ij}-\theta _{ij}\right) \\
Q_{i} = \displaystyle \sum_{j=1}^{3} Y_{ij}V_{i}V_{j}\cos \left( \delta _{ij}-\theta _{ij}\right) \\
\end{array}
\right. \\[ 5pt ]
&(ホ)& \left\{
\begin{array}{l}
P_{i} = \displaystyle \sum_{j=1}^{3} Y_{ij}V_{i}V_{j}\cos \left( \delta _{ij}-\theta _{ij}\right) \\
Q_{i} = \displaystyle \sum_{j=1}^{3} Y_{ij}V_{i}V_{j}\sin \left( \delta _{ij}-\theta _{ij}\right) \\
\end{array}
\right. &(ヘ)& \left\{
\begin{array}{l}
P_{i} = \displaystyle \sum_{j=1}^{3} Y_{ij}V_{i}V_{j}\sin \left( \delta _{ij}+\theta _{ij}\right) \\
Q_{i} = \displaystyle \sum_{j=1}^{3} Y_{ij}V_{i}V_{j}\cos \left( \delta _{ij}+\theta _{ij}\right) \\
\end{array}
\right. \\[ 5pt ]
&(ト)& \mathrm {LFC} &(チ)& 0 \\[ 5pt ]
&(リ)& -b_{12}\delta _{21}-b_{23}\delta _{23} &(ヌ)& ノード電圧の位相 \\[ 5pt ]
&(ル)& \frac {\pi }{2} &(ヲ)& 電圧降下 \\[ 5pt ]
&(ワ)& \mathrm {GOV} &(カ)& b_{12}\delta _{21}+b_{23}\delta _{23} \\[ 5pt ]
&(ヨ)& -\frac {\pi }{2} &(タ)& 送電損失 \\[ 5pt ]
&(レ)& 無効電力出力 &(ソ)& \mathrm {AVR} \\[ 5pt ]
&(ツ)& ノード電圧の大きさ && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電力系統の潮流計算に関する問題です。
潮流計算の知識も必要であり,文章を読解しながらやや複雑な計算をこなさなければならない難問です。
\( \ \mathrm {B} \ \)問題は配点も高く,合格のためには逃げることが許されない問題ですので,じっくりと読解し解いていくようにして下さい。
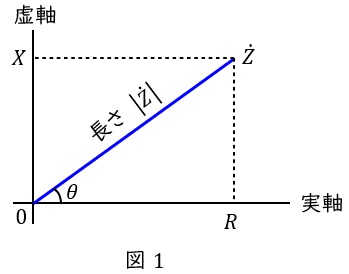
1.複素平面における複素数の表記方法
図1のような複素空間上の値\( \ \dot Z =R+\mathrm {j}X \ \)において,以下のような表記方法が定義されます。
ただし,\( \ \dot Z \ \)の絶対値\( \ \left| \dot Z\right| = \sqrt {R^{2}+X^{2}} \ \),\( \ \dot Z \ \)と実軸となす角を\( \ \theta \ \)とします。
①直交座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \left( \cos \theta +\mathrm {j}\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
②指数表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \mathrm {e}^{\mathrm {j}\theta } \\[ 5pt ]
\end{eqnarray}
\]
ただし,
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
であり,これをオイラーの公式といいます。
③極座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| ∠\theta \\[ 5pt ]
\end{eqnarray}
\]
2.複素電力
単相線路において,送電端電圧を\( \ {\dot V}_{\mathrm {s}} \ \mathrm {[V]} \ \),受電端電圧を\( \ {\dot V}_{\mathrm {r}} \ \mathrm {[V]} \ \),線路電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると,受電端への送電電力\( \ P+\mathrm {j}Q \ \mathrm {[V\cdot A]} \ \)は遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&{\dot V}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。ただし,\( \ \overline {\dot I} \ \)は\( \ \dot I \ \)の共役複素数であり,\( \ \dot I =I_{\mathrm {r}}+\mathrm {j}I_{\mathrm {i}} \ \)であるとき,\( \ \overline {\dot I}=I_{\mathrm {r}}-\mathrm {j}I_{\mathrm {i}} \ \)となります。
【解答】
(1)解答:イ
問題図より,ノード\( \ 1 \ \)→ノード\( \ 2 \ \)間を流れる電流は\( \ {\dot I}_{1} \ \),ノード\( \ 3 \ \)→ノード\( \ 2 \ \)間を流れる電流は\( \ {\dot I}_{3} \ \)であるから,キルヒホッフの法則の電圧則より,
\[
\begin{eqnarray}
{\dot V}_{1}-{\dot V}_{2} &=& \frac {{\dot I}_{1}}{{\dot y}_{12}} && \\[ 5pt ]
{\dot I}_{1} &=& {\dot y}_{12}{\dot V}_{1}-{\dot y}_{12}{\dot V}_{2} &・・・・・・・・・・・・・・・ ①& \\[ 5pt ]
{\dot V}_{3}-{\dot V}_{2} &=& \frac {{\dot I}_{3}}{{\dot y}_{23}}&& \\[ 5pt ]
{\dot I}_{3} &=& -{\dot y}_{23}{\dot V}_{2}+{\dot y}_{23}{\dot V}_{3} &・・・・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
となり,キルヒホッフの法則の電流則より\( \ {\dot I}_{1}+{\dot I}_{2}+{\dot I}_{3}=0 \ \)であるから,
\[
\begin{eqnarray}
{\dot I}_{2} &=& -{\dot I}_{1}-{\dot I}_{3} \\[ 5pt ]
&=& -\left( {\dot y}_{12}{\dot V}_{1}-{\dot y}_{12}{\dot V}_{2}\right) -\left( -{\dot y}_{23}{\dot V}_{2}+{\dot y}_{23}{\dot V}_{3}\right) \\[ 5pt ]
&=& -{\dot y}_{12}{\dot V}_{1}+{\dot y}_{12}{\dot V}_{2}+{\dot y}_{23}{\dot V}_{2}-{\dot y}_{23}{\dot V}_{3} \\[ 5pt ]
&=& -{\dot y}_{12}{\dot V}_{1}+\left( {\dot y}_{12}+{\dot y}_{23}\right) {\dot V}_{2}-{\dot y}_{23}{\dot V}_{3} ・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
となる。①~③より,各ノード\( \ i \ \)に注入される電流\( \ {\dot I}_{i} \ \)を行列式で表すと,
\[
\begin{eqnarray}
\begin{bmatrix}
{\dot I}_{1} \\
{\dot I}_{2} \\
{\dot I}_{3} \\
\end{bmatrix} &=& \begin{bmatrix}
{\dot y}_{12} & -{\dot y}_{12} & 0 \\
-{\dot y}_{12} & {\dot y}_{12}+{\dot y}_{23} & -{\dot y}_{23} \\
0 & -{\dot y}_{23} & {\dot y}_{23} \\
\end{bmatrix}\begin{bmatrix}
{\dot V}_{1} \\
{\dot V}_{2} \\
{\dot V}_{3} \\
\end{bmatrix} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ホ
ノード\( \ 1 \ \)について考える。問題に与えられているノードの行列式より,
\[
\begin{eqnarray}
{\dot I}_{1} &=& {\dot Y}_{11}{\dot V}_{1}+{\dot Y}_{12}{\dot V}_{2}+{\dot Y}_{13}{\dot V}_{3} \\[ 5pt ]
&=& Y_{11}∠\theta_{11} V_{1}∠\delta _{1} +Y_{12}∠\theta _{12} V_{2}∠\delta _{2} +Y_{13}∠\theta _{13} V_{3}∠\delta _{3} \\[ 5pt ]
&=& Y_{11}V_{1}∠\left( \delta _{1}+\theta_{11} \right) +Y_{12}V_{2}∠\left( \delta _{2}+\theta _{12} \right) +Y_{13}V_{3}∠\left( \delta _{3}+\theta _{13} \right) \\[ 5pt ]
\end{eqnarray}
\]
となるから,ノード\( \ 1 \ \)に供給される複素電力\( \ P_{1}+\mathrm {j}Q_{1} \ \)は,ワンポイント解説「2.複素電力」の通り,
\[
\begin{eqnarray}
P_{1}+\mathrm {j}Q_{1} &=& {\dot V}_{1}\overline {{\dot I}_{1}} \\[ 5pt ]
&=& V_{1}∠\delta _{1}\left\{ Y_{11}V_{1}∠\left( -\delta _{1}-\theta_{11} \right) +Y_{12}V_{2}∠\left( -\delta _{2}-\theta _{12} \right) +Y_{13}V_{3}∠\left( -\delta _{3}-\theta _{13} \right) \right\} \\[ 5pt ]
&=& Y_{11}V_{1}V_{1}∠\left( \delta _{1}-\delta _{1}-\theta_{11} \right) +Y_{12}V_{1}V_{2}∠\left( \delta _{1}-\delta _{2}-\theta _{12} \right) +Y_{13}V_{1}V_{3}∠\left( \delta _{1}-\delta _{3}-\theta _{13} \right) \\[ 5pt ]
&=& Y_{11}V_{1}V_{1}∠\left( \delta _{11}-\theta_{11} \right) +Y_{12}V_{1}V_{2}∠\left( \delta _{12}-\theta _{12} \right) +Y_{13}V_{1}V_{3}∠\left( \delta _{13}-\theta _{13} \right) \\[ 5pt ]
\end{eqnarray}
\]
となり,これを直交座標表記にすれば,
\[
\begin{eqnarray}
P_{1}+\mathrm {j}Q_{1} &=& Y_{11}V_{1}V_{1}\left\{ \cos \left( \delta _{11}-\theta_{11} \right) +\mathrm {j} \sin \left( \delta _{11}-\theta_{11} \right) \right\} +Y_{12}V_{1}V_{2}\left\{ \cos \left( \delta _{12}-\theta _{12} \right) +\mathrm {j} \sin \left( \delta _{12}-\theta _{12} \right) \right\} +Y_{13}V_{1}V_{3}\left\{ \cos \left( \delta _{13}-\theta _{13} \right) +\mathrm {j} \sin \left( \delta _{13}-\theta _{13} \right) \right\}\\[ 5pt ]
\end{eqnarray}
\]
となる。ノード\( \ 2 \ \)及びノード\( \ 3 \ \)についても全く同様に求められ,定式化すると,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
P_{i} = \displaystyle \sum_{j=1}^{3} Y_{ij}V_{i}V_{j}\cos \left( \delta _{ij}-\theta _{ij}\right) \\
Q_{i} = \displaystyle \sum_{j=1}^{3} Y_{ij}V_{i}V_{j}\sin \left( \delta _{ij}-\theta _{ij}\right) \\
\end{array}
\right.
\end{eqnarray}
\]
と求められる。
(3)解答:ル
ブランチの抵抗成分が無視できる場合,
\[
\begin{eqnarray}
{\dot Y}_{ij} &=& Y_{ij} ∠\theta _{ij} \\[ 5pt ]
&=& Y_{ij} \left( \cos \theta _{ij}+\mathrm {j} \sin \theta _{ij}\right) \\[ 5pt ]
&=& \mathrm {j} Y_{ij} \sin \theta _{ij} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \theta _{ij}=\frac {\pi }{2} \ \)と求められる。
(4)解答:カ
(2)解答式より,
\[
\begin{eqnarray}
P_{2} &=& Y_{21}V_{2}V_{1}\cos \left( \delta _{21}-\theta _{21}\right) +Y_{22}V_{2}V_{2}\cos \left( \delta _{22}-\theta _{22}\right) +Y_{23}V_{2}V_{3}\cos \left( \delta _{23}-\theta _{23}\right) \\[ 5pt ]
&=& y_{12}\times 1.0 \times 1.0\cos \left( \delta _{21}-\frac {\pi }{2}\right) +\left( y_{12}+y_{23}\right) \times 1.0 \times 1.0\cos \left( 0-\frac {\pi }{2}\right) + y_{23}\times 1.0 \times 1.0\cos \left( \delta _{23}-\frac {\pi }{2}\right) \\[ 5pt ]
&=& b_{12}\sin \delta _{21} +\left( b_{12}+b_{23}\right) \times 0 +b_{23} \sin \delta _{23} \\[ 5pt ]
&≈& b_{12} \delta _{21} +b_{23} \delta _{23} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ソ
題意より解答候補は,(ト)\( \ \mathrm {LFC} \ \),(ワ)\( \ \mathrm {GOV} \ \),(ソ)\( \ \mathrm {AVR} \ \),になると思います。
このうち潮流計算において,発電機が有する機能として最も適当なのは\( \ \mathrm {AVR} \ \)(自動電圧調整器)です。\( \ \mathrm {LFC} \ \)は負荷周波数制御という電力制御で潮流計算とは直接の関係なく,\( \ \mathrm {GOV} \ \)はガバナという発電機の回転速度を一定にするために調整する装置で,有効電力出力を拘束条件とする潮流計算では関係ありません。
(6)解答:ツ
題意より解答候補は,(ヌ)ノード電圧の位相,(レ)無効電力出力,(ツ)ノード電圧の大きさ,になると思います。
\( \ \mathrm {AVR} \ \)を有する発電機が接続するノードではノード電圧の大きさを一定に保つことができるので拘束条件として考えることができます。
(7)解答:タ
題意より解答候補は,(ヲ)電圧降下,(タ)送電損失,になると思います。
潮流計算においては電力系統全体に生じる送電損失が未知量となるため、その調整用としてスラックノードというものが設定されます。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん