【問題】
【難易度】★★★☆☆(普通)
次の文章は,一般電気事業者(現:一般送配電事業者)の電力系統内における停電事故の拡大に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる語句を解答群の中から選び,その記号を記述用紙の解答欄に記入しなさい。
電力系統の一部に生じた単純な事故が引き金となり,これに悪条件が重なると次から次へと事故が拡大することがある。
このように事故を拡大させる悪条件(技術的要因)としては,次のようなことが考えられる。
① 有効電力の需給不均衡による\( \ \fbox { (1) } \ \)の異常変化
② ある送電線の\( \ \fbox { (2) } \ \)による連系する他の送電線の連鎖的な\( \ \fbox { (2) } \ \)
③ 送電系統の脱調(\( \ \fbox { (3) } \ \)の崩壊)
④ 無効電力の需給不均衡や電圧の異常変化
⑤ \( \ \fbox { (4) } \ \)の伝播による異地点,異相地絡の発生
上記①の要因による事故を例にとると,電源線の事故によって電源が系統から切り離された場合には,系統の\( \ \fbox { (5) } \ \)が不足するため,\( \ \fbox { (1) } \ \)は低下していく。このような状態が継続して,健全なタービン発電機に機械的振動などの悪影響を及ぼすような状況になった場合には,タービン発電機を保護するため解列させることから,やがては停電事故が拡大していくということが起こりうる。
最近の電力系統は,いくつもの単独系統が連系された複合系統となっており,適切な\( \ \fbox { (6) } \ \)が設置されているが,常に\( \ \fbox { (7) } \ \)の脅威を内蔵しており,十分な注意を払い運用していかなければならない。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& 安定度 &(ロ)& 保護リレーシステム &(ハ)& 異常電圧 \\[ 5pt ]
&(ニ)& 高調波 &(ホ)& 需 要 &(ヘ)& 供給力 \\[ 5pt ]
&(ト)& 不足電圧 &(チ)& 無効電力 &(リ)& 信頼度 \\[ 5pt ]
&(ヌ)& 瞬時電圧低下 &(ル)& 過負荷 &(ヲ)& 位 相 \\[ 5pt ]
&(ワ)& 連鎖事故 &(カ)& 安全係数 &(ヨ)& 系統周波数 \\[ 5pt ]
&(タ)& 無効電力補償装置 &(レ)& 短 絡 &(ツ)& 絶縁破壞 \\[ 5pt ]
&(ネ)& 電圧フリッカ &(ナ)& 力 率 &(ム)& 絶縁劣化診断装置 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電力系統内における停電事故の拡大に関する問題です。
様々な知識を複合した内容で,受験生の総合力が求められる問題です。ただし,問題文と解答群から適当な選択肢が相当絞れるので,しっかりと文脈を考えていくことが重要です。
ワンポイント解説では代表的な内容を紹介していますが,範囲が広くここですべてを網羅することは困難なので,多くの問題を解くことで本問を解くための知識を身に着けていってください。
1.同期発電機の出力
同期発電機の内部誘導起電力が\( \ E \ \mathrm {[V]} \ \),端子電圧が\( \ V \ \mathrm {[V]} \ \),\( \ 1 \ \)相あたりの同期リアクタンスが\( \ X \ \mathrm {[\Omega ]} \ \)(抵抗分は無視できるものとします),電機子電流が\( \ I \ \mathrm {[A]} \ \)であるとすると,回路図は図1,ベクトル図は図2のように描くことができます。ただし,\( \ \delta \ \mathrm {[rad]} \ \)は内部誘導起電力と端子電圧の相差角,\( \ \theta \ \mathrm {[rad]} \ \)は力率角です。
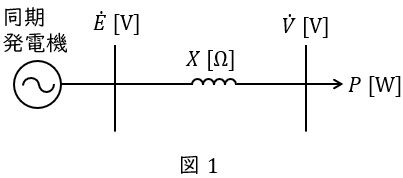
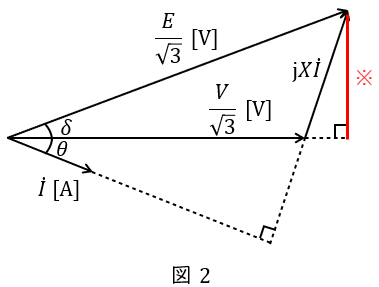
このとき,発電機の出力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P&=&\sqrt {3} VI\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
で求めることができ,図2の※線を求める式より,
\[
\begin{eqnarray}
XI\cos \theta &=&\frac {E}{\sqrt {3}}\sin \delta \\[ 5pt ]
I\cos \theta &=&\frac {E}{\sqrt {3}X}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
P&=&\sqrt {3} VI\cos \theta \\[ 5pt ]
&=&\sqrt {3} V\cdot \frac {E}{\sqrt {3}X}\sin \delta \\[ 5pt ]
&=&\frac {EV}{X}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となります。上式は\( \ P=\sqrt {3} VI\cos \theta \ \)と合わせて公式として覚えておきましょう。
2.同期化力
同期発電機の同期外れの起こりにくさすなわち定態安定度を表す指標で,出力\( \ P \ \mathrm {[W]} \ \)を相差角\( \ \delta \ \mathrm {[rad]} \ \)で微分した\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta } \ \)で求められます。したがって,
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}\delta }&=&\frac {EV}{X}\cos \delta \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta }>0 \ \)のとき安定,\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta }<0 \ \)のとき不安定,すなわち\( \ \displaystyle 0 < \delta < \frac {\pi }{2} \ \)のとき安定,\( \ \displaystyle \frac {\pi }{2} < \delta < \pi \ \)のとき不安定となります。
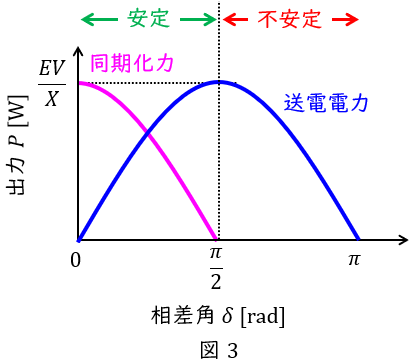
3.系統周波数特性係数
電力系統の需要と供給の不均衡が発生すると,これに応じ周波数も変化します。その電力と周波数の関係を系統周波数特性係数といい,一般に\( \ K \ \mathrm {[MW / Hz]} \ \)もしくは\( \ K^{\prime } \ \mathrm {[MW / 0.1Hz]} \ \)で表され,電源の容量が変化した際に系統周波数がどれだけ変化するかを示す指標となります。定量的に示すと,電源が\( \ \Delta P \ \mathrm {[MW]} \ \)変化したときの系統周波数の変化\( \ \Delta f \ \mathrm {[Hz]} \ \)は,
\[
\begin{eqnarray}
\Delta f &=&\frac {\Delta P}{K} \\[ 5pt ]
&=&\frac {\Delta P}{10K^{\prime }} \\[ 5pt ]
\end{eqnarray}
\]
となります。
また,図4のように\( \ 2 \ \)系統以上の系統周波数特性係数が与えられている場合について,系統周波数特性係数\( \ K_{\mathrm {A}} \ \mathrm {[MW / Hz]} \ \)の系統\( \ \mathrm {A} \ \)と系統周波数特性係数\( \ K_{\mathrm {B}} \ \mathrm {[MW / Hz]} \ \)の系統\( \ \mathrm {B} \ \)があった場合,全体の系統周波数特性係数\( \ K \ \mathrm {[MW / Hz]} \ \)は,
\[
\begin{eqnarray}
K&=&K_{\mathrm {A}}+K_{\mathrm {B}} \\[ 5pt ]
\end{eqnarray}
\]
となり,例えば,系統\( \ \mathrm {A} \ \)で\( \ \Delta P_{\mathrm {A}} \ \mathrm {[MW]} \ \)変化があったときの系統全体の周波数変化量\( \ \Delta f \ \mathrm {[Hz]} \ \)は,
\[
\begin{eqnarray}
\Delta f &=&\frac {\Delta P_{\mathrm {A}}}{K} \\[ 5pt ]
&=&\frac {\Delta P_{\mathrm {A}}}{K_{\mathrm {A}}+K_{\mathrm {B}}} \\[ 5pt ]
\end{eqnarray}
\]
であり,このときの連系線\( \ \mathrm {A-B} \ \)の潮流変化\( \ \Delta P_{\mathrm {T}} \ \mathrm {[MW]} \ \)は,
\[
\begin{eqnarray}
\Delta P_{\mathrm {T}} &=&\Delta f K_{\mathrm {B}} \\[ 5pt ]
&=&\frac {K_{\mathrm {B}} }{K_{\mathrm {A}}+K_{\mathrm {B}}}\Delta P_{\mathrm {A}} \\[ 5pt ]
\end{eqnarray}
\]
となります。

4.系統周波数変動時の汽力発電プラントへの影響
同期機の回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)は,極数を\( \ p \ \),周波数を\( \ f \ \mathrm {[Hz]} \ \)とすると\( \ \displaystyle N=\frac {120f}{p} \ \)の関係があり,系統周波数が変動すると,タービン発電機の回転速度が変動します。これにより以下の問題点が生じる可能性があります。
①タービン(特に低圧タービン)の振動
タービンの動翼の共振周波数と回転速度が共振をすることで振動が上昇する可能性があります。
②発電機の出力変動
速度調定率により周波数が変動すると出力が変化するため,周波数が低下すると出力が上昇し,周波数が上昇すると出力は低下します。
③タービン軸受油圧の低下
主油ポンプがタービン直結式のものも多いため,回転速度が低下すると軸受油圧が低下し,軸受損傷やユニットトリップに至る可能性があります。
④発電機補機の出力上昇,減退
周波数が変化すると補機の誘導電動機の回転速度が変化するため,回転速度が変化すると出力が変化します。
⑤ボイラ燃焼制御,給水制御の不安定化
補機の出力が変化するため,ボイラの燃焼制御や給水制御が不安定となる可能性があります。
⑥発電機・変圧器の過励磁
発電機や変圧器鉄心の磁束密度は\( \ V / f \ \)にほぼ比例し,\( \ V / f \ \)をほぼ一定に保つ必要がありますが,周波数が低下すると\( \ V / f \ \)が大きくなり,磁束密度が増えます。したがって,過励磁により鉄損が増加し過熱する可能性があります。
【解答】
(1)解答:ヨ
題意より解答候補は,(ヲ)位相,(ヨ)系統周波数,(ナ)力率,等になると思います。
ワンポイント解説「3.系統周波数特性係数」の通り,有効電力の需給不均衡により発生するのは系統周波数の異常変化となります。
(2)解答:ル
題意より解答候補は,(ハ)異常電圧,(ヌ)瞬時電圧低下,(ル)過負荷,(レ)短絡,(ツ)絶縁破壞,等になると思います。
このうち事故を拡大させる文章として成立するのは過負荷となります。一般にある送電線が過負荷になると潮流の変化が発生し,連系する他の送電線も過負荷になります。
(3)解答:イ
題意より解答候補は,(イ)安定度,(リ)信頼度,(カ)安全係数,等になると思います。
脱調とは,電力系統に接続された同期発電機が周波数と同期した関係を保てなくなり同期外れとなる現象で,ワンポイント解説「2.同期化力」の通り,安定度が関連性の高い用語となります。
(4)解答:ハ
題意より解答候補は,(ハ)異常電圧,(ニ)高調波,(ネ)電圧フリッカ,等になると思います。
このうち伝播により異地点,異相地絡の発生が起こるのは異常電圧となります。この空欄は解答群から消去法で導出できると良いかと思います。
(5)解答:ヘ
題意より解答候補は,(ホ)需要,(ヘ)供給力,(チ)無効電力,等になると思います。
電源線の事故によって電源が系統から切り離された場合には,系統の供給力が不足することになり,周波数が低下していきます。
(6)解答:ロ
題意より解答候補は,(ロ)保護リレーシステム,(タ)無効電力補償装置,(ム)絶縁劣化診断装置,等になると思います。
電力系統は,いくつもの単独系統が連系された複合系統となっており,適切な保護リレーシステムが設置されています。この空欄も解答群から消去法で導出できると良いかと思います。
(7)解答:ワ
題意より解答候補は,(ハ)異常電圧,(ト)不足電圧,(ワ)連鎖事故,(ツ)絶縁破壞,等になると思います。
このうち有効電力の需給不均衡により保護リレーシステムが働かない場合に発生するのは連鎖事故となります。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん