【問題】
【難易度】★★★☆☆(普通)
次の文章は,同期発電機に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
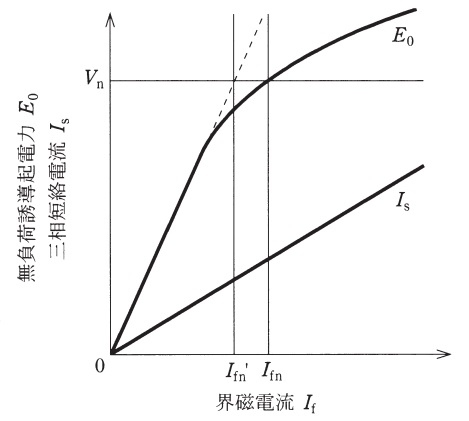
図は,三相同期発電機の界磁電流\( \ I_{\mathrm {f}} \ \)に対する\( \ 1 \ \)相分の無負荷誘導起電力\( \ E_{0} \ \)及び三相短絡電流\( \ I_{\mathrm {s}} \ \)の特性である。無負荷誘導起電力\( \ E_{0} \ \)と界磁電流\( \ I_{\mathrm {f}} \ \)との間の関係は,
\[
\begin{eqnarray}
E_{0}&=&\frac {\omega MI_{\mathrm {f}}}{\sqrt {2}} \\[ 5pt ]
\end{eqnarray}
\]
で与えられる。ただし,\( \ \omega \ \)は電気角速度,\( \ M \ \)は界磁巻線と電機子巻線\( \ 1 \ \)相との間の相互インダクタンスである。しかし,実際の無負荷誘導起電力には,図中の\( \ E_{0} \ \)のように飽和特性を生じる。これは,相互インダクタンス\( \ M \ \)の非線形性に起因するもので,界磁電流の増加に伴って\( \ \fbox { (1) } \ \)が減少することにより生じる。一般に,定格電圧\( \ V_{\mathrm {n}} \ \)を得るための界磁電流\( \ I_{\mathrm {fn}} \ \)は,飽和特性を考慮しない場合の界磁電流\( \ I_{\mathrm {fn}}^{\prime } \ \)に比べて\( \ 5 ~15 \ [%] \ \)程度大きい。
一方,三相短絡電流は界磁電流にほぼ比例し,通常の界磁電流の範囲では,飽和特性の影響は現れない。これは,電機子電流の\( \ \fbox { (2) } \ \)によるものである。同期リアクタンス\( \ X_{\mathrm {s}} \ \)及び巻線抵抗\( \ r \ \)を用いると,三相短絡電流は,\( \ {\dot I}_{\mathrm {s}}=\fbox { (3) } \ \)である。この式を電機子巻線\( \ 1 \ \)相の自己インダクタンス\( \ L_{0} \ \)及び漏れインダクタンス\( \ l \ \)で書き換えると,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {s}}&=&\frac {\displaystyle \frac {\omega MI_{\mathrm {f}}}{\sqrt {2}}}{\displaystyle r+\mathrm {j}\omega \left( \frac {3}{2}L_{0}+l\right) } \\[ 5pt ]
\end{eqnarray}
\]
となる。界磁電流による\( \ \fbox { (4) } \ \)は\( \ \displaystyle \frac { MI_{\mathrm {f}}}{\sqrt {2}} \ \),短絡電流による\( \ \fbox { (4) } \ \)は\( \ \displaystyle \frac {3}{2}L_{0}I_{\mathrm {s}} \ \)であるので,界磁及び電機子の漏れインダクタンスと巻線抵抗を無視すると,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&\frac {\sqrt {2}}{3}KI_{\mathrm {f}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ただし,\( \ K \ \)は界磁巻線の電機子巻線に対する\( \ \fbox { (5) } \ \)である。
上式には,\( \ M \ \)や\( \ L_{0} \ \)などの磁気的に非線形な係数を含まないので,界磁電流\( \ I_{\mathrm {f}} \ \)と三相短絡電流\( \ I_{\mathrm {s}} \ \)とは比例関係になる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& 磁界 &(ロ)& 磁束鎖交数 &(ハ)& 透磁率 \\[ 5pt ]
&(ニ)& \frac {E_{0}}{\displaystyle r+\mathrm {j}\sqrt {\frac {3}{2}}X_{\mathrm {s}}} &(ホ)& 渦電流 &(ヘ)& 交差磁化作用 \\[ 5pt ]
&(ト)& 結合係数 &(チ)& 起磁力 &(リ)& 巻数比 \\[ 5pt ]
&(ヌ)& 増磁作用 &(ル)& \frac {E_{0}}{\displaystyle r+\mathrm {j}\frac {3X_{\mathrm {s}}}{2}} &(ヲ)& 磁気抵抗 \\[ 5pt ]
&(ワ)& \frac {E_{0}}{\displaystyle r+\mathrm {j}X_{\mathrm {s}}} &(カ)& 減磁作用 &(ヨ)& 短絡比 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
問題文の内容は専門書に書いてあるような内容ですが,空欄とされているのはそれほど難解なものではありません。興味のある方は知識を深めるために各式の導出等を勉強しても良いかもしれませんが,電験で出題される可能性は低いと思います。
1.同期発電機の特性曲線
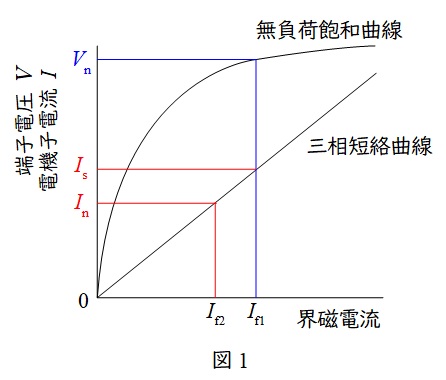
同期発電機は図1のような無負荷飽和曲線と三相短絡曲線の特性があります。
無負荷誘導起電力は界磁電流が増加するに従い,飽和する特性がありますが,これは界磁電流が増加し鎖交磁束数が増加すると,鉄心が磁気飽和し,透磁率が減少するためです。
2.同期発電機の等価回路
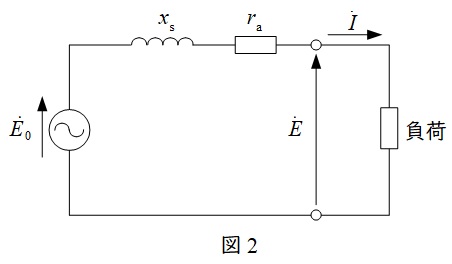
同期発電機の等価回路は,無負荷誘導起電力を\( \ E_{0} \ \),端子電圧を\( \ E \ \),電機子巻線抵抗を\( \ r_{\mathrm {a}} \ \),同期リアクタンスを\( \ x_{\mathrm {s}} \ \)とすると,図2のようになります。本問では無視をしていませんが,一般に電機子巻線抵抗\( \ r_{\mathrm {a}} \ \)は小さいので無視する方が多いです。
【解答】
(1)解答:ハ
題意より,解答候補は(イ)磁界,(ロ)磁束鎖交数,(ハ)透磁率,(ホ)渦電流,(チ)起磁力,(ヲ)磁気抵抗,となると思います。ワンポイント解説「1.同期発電機の特性曲線」の通り,無負荷誘導起電力の飽和特性は透磁率が減少することによって生じます。
(2)解答:カ
題意より,解答候補は(ヘ)交差磁化作用,(ヌ)増磁作用,(カ)減磁作用,となると思います。ワンポイント解説「2.同期発電機の等価回路」の通り,同期発電機は電機子巻線抵抗\( \ r_{\mathrm {a}} \ \)が小さいので無視でき,電機子電流は無負荷誘導起電力より\( \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)遅れ位相となります。電機子電流が遅れであると減磁作用のため,界磁磁束は磁気飽和せず,短絡電流が直線となります。
(3)解答:ワ
ワンポイント解説「2.同期発電機の等価回路」の図2の通り等価回路は表される。三相短絡電流は負荷に何もつないでいない時の電流なので,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {s}}&=&\frac {E_{0}}{\displaystyle r+\mathrm {j}X_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
(4)解答:ロ
題意より,解答候補は(イ)磁界,(ロ)磁束鎖交数,(ホ)渦電流,(チ)起磁力,となると思います。界磁電流と短絡電流に関連するのは磁束鎖交数になります。
(5)解答:リ
題意より,解答候補は(ト)結合係数,(リ)巻数比,等になると思います。\( \ \displaystyle I_{\mathrm {s}}=\frac {\sqrt {2}}{3}KI_{\mathrm {f}} \ \)の\( \ K \ \)は巻数比となります。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん