【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,変換器の多重接続に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
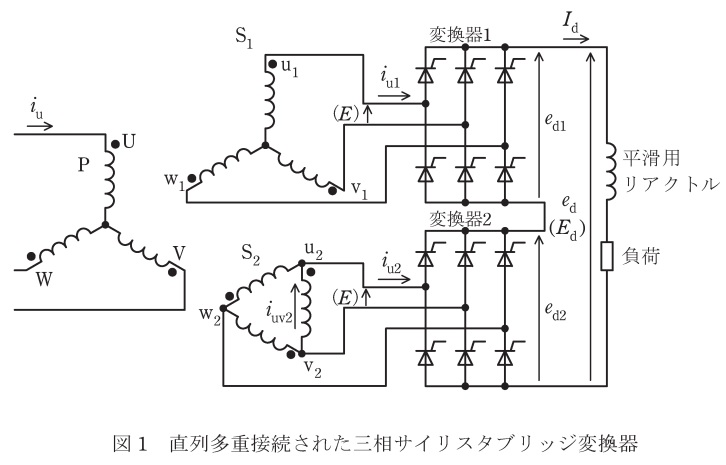
図1には,入力交流線間電圧の位相を\( \ 30° \ \)ずらし,同じ制御遅れ角\( \ \alpha \ \)で動作する\( \ 2 \ \)組の三相サイリスタブリッジ変換器を直列に多重接続した回路を示す。変換器\( \ 1 \ \)の入力電圧位相は変換器\( \ 2 \ \)の入力電圧位相に対して\( \ 30° \ \)進んでいる。ここで,平滑用リアクトルのインダクタンスは十分に大きく,直流電流\( \ I_{\mathrm {d}} \ \)は一定とする。また,電源インピーダンスなどによる電流重なり現象は無視するものとする。
各ブリッジの入力交流線間電圧は同じ実効値\( \ E \ \)とするので,変圧器の二次巻線\( \ \mathrm {S}_{1} \ \)と\( \ \mathrm {S}_{2} \ \)の巻数の比は\( \ 1 \ : \ \fbox { (1) } \ \)である。このとき,各ブリッジの直流電圧\( \ e_{\mathrm {d1}} \ \),\( \ e_{\mathrm {d2}} \ \)の平均値は\( \ \fbox { (2) } \ \)である。また,多重化により直流電圧\( \ e_{\mathrm {d}} \ \)(直流平均電圧を\( \ E_{\mathrm {d}} \ \)とする)は直流電圧\( \ e_{\mathrm {d1}} \ \)と\( \ e_{\mathrm {d2}} \ \)を加算した電圧であるので,\( \ e_{\mathrm {d}} \ \)の電圧リプル率(直流平均電圧に対するリプル振幅の比率)は\( \ e_{\mathrm {d1}} \ \),\( \ e_{\mathrm {d2}} \ \)のそれよりも小さくなり,リプル成分の繰り返し周期は基本波の\( \ \fbox { (3) } \ \)相当となる。
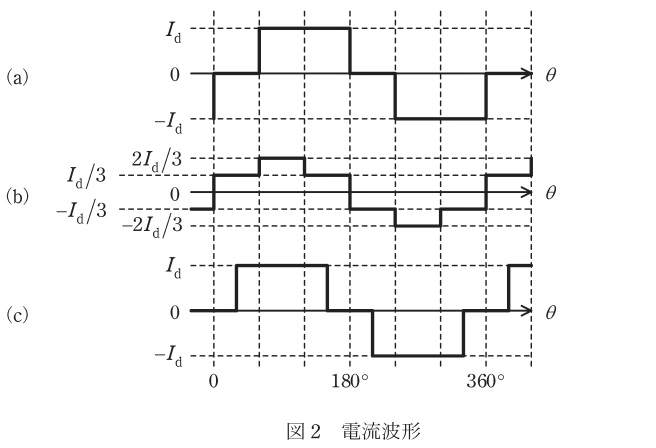
図2には,変圧器二次側の各部の電流\( \ i_{\mathrm {u1}} \ \),\( \ i_{\mathrm {u2}} \ \)及び\( \ i_{\mathrm {uv2}} \ \)の波形を示す。このうち電流\( \ i_{\mathrm {u2}} \ \)の波形は図2の\( \ \fbox { (4) } \ \)である。変圧器一次側に流れる電流\( \ i_{\mathrm {u}} \ \)に含まれる低次の高調波電流は\( \ \fbox { (5) } \ \)成分の電流となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 1.35E\cos \alpha &(ロ)& 1 &(ハ)& 5 \ 次,7 \ 次,11 \ 次,13 \ 次,\cdots \\[ 5pt ]
&(ニ)& 60° &(ホ)& 120° &(ヘ)& 11 \ 次,13 \ 次,\cdots \\[ 5pt ]
&(ト)& 0.90E\cos \alpha &(チ)& \frac {1}{\sqrt {3}} &(リ)& (\mathrm {a}) \\[ 5pt ]
&(ヌ)& 30° &(ル)& (\mathrm {b}) &(ヲ)& 0.45E\cos \alpha \\[ 5pt ]
&(ワ)& \sqrt {3} &(カ)& (\mathrm {c}) && \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ヨ)& 3 \ 次,5 \ 次,7 \ 次,11 \ 次,13 \ 次,\cdots \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ 12 \ \)パルス三相サイリスタブリッジ変換器の動作原理に関する問題です。
変圧器を\( \ \mathrm {Y} – \Delta \ \)接続することにより,電圧の位相が\( \ 30° \ \)ずれることを利用してより滑らかな直流電流を得ることができるようにしたものとなります。
少し難易度は高いですが,二次試験の機械制御科目で平成28年に\( \ 12 \ \)パルスサイリスタブリッジ変換器の問題が出題されているので,過去問を勉強されている方であればイメージがしやすい問題であったかもしれません。
1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係
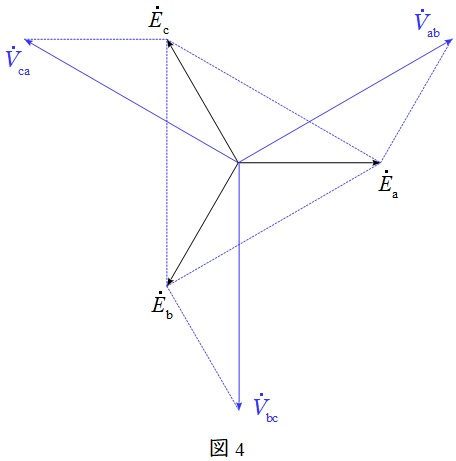
図3のような三相対称電源がある時,線間電圧と相電圧の関係は図4のベクトル図のようになり,線間電圧の大きさ\( \ V \ \)は相電圧の大きさ\( \ E \ \)と比較すると,
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=&\sqrt {3}E_{\mathrm {a}} \\[ 5pt ]
V_{\mathrm {bc}} &=&\sqrt {3}E_{\mathrm {b}} \\[ 5pt ]
V_{\mathrm {ca}} &=&\sqrt {3}E_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)進みであることが分かります。

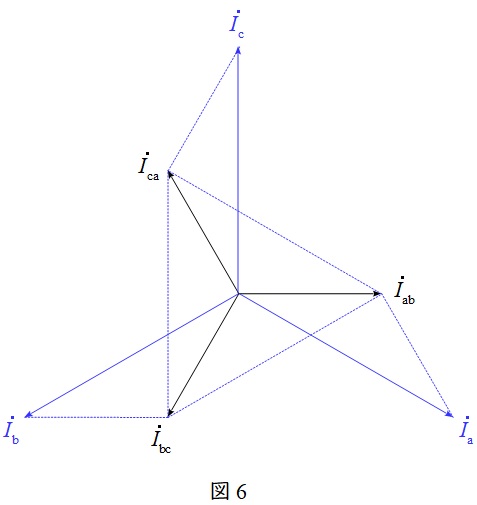
2.\( \ \Delta \ \)結線における相電流と線電流の関係
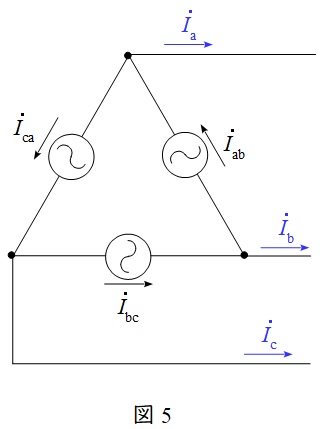
図5のような三相対称電源がある時,線電流と相電流の関係は図6のベクトル図のようになり,線電流の大きさは相電流の大きさと比較すると,
\[
\begin{eqnarray}
I_{\mathrm {a}} &=&\sqrt {3}I_{\mathrm {ab}} \\[ 5pt ]
I_{\mathrm {b}} &=&\sqrt {3}I_{\mathrm {bc}} \\[ 5pt ]
I_{\mathrm {c}} &=&\sqrt {3}I_{\mathrm {ca}} \\[ 5pt ]
\end{eqnarray}
\]
かつ\( \ \displaystyle \frac {\pi }{6} \)(30°)遅れであることが分かります。
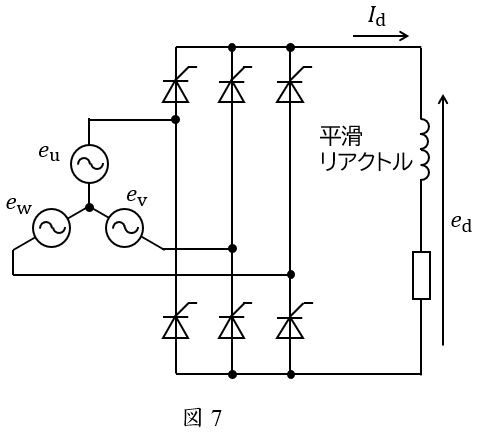
3.三相サイリスタブリッジ整流回路の平均出力電圧\( \ E_{\mathrm {d}} \ \)
図7のような三相サイリスタブリッジ整流回路について考えます。
ただし,電源の電圧は\( \ e_{\mathrm {u}} \ \)を基準として,
\[
\begin{eqnarray}
e_{\mathrm {u}} &=&\sqrt {2}E \sin \theta \\[ 5pt ]
e_{\mathrm {v}} &=&\sqrt {2}E \sin \left( \theta -\frac {2}{3}\pi \right) \\[ 5pt ]
e_{\mathrm {w}} &=&\sqrt {2}E \sin \left( \theta -\frac {4}{3}\pi \right) \\[ 5pt ]
\end{eqnarray}
\]
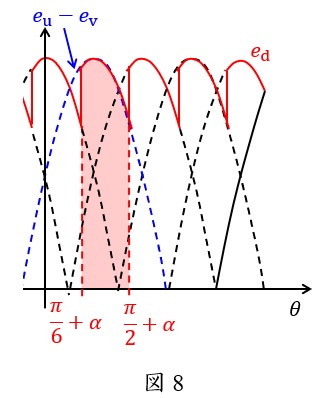
とします。サイリスタの制御角を\( \ \alpha \ \)とすると,出力電圧は図8のようになります。
このとき,出力電圧は周期\( \ \displaystyle \frac {\pi }{3} \ \)で繰り返しているので,その平均出力電圧\( \ E_{\mathrm {d}} \ \)は図8で示した領域の平均値を求めればよいことになります。
図8において,
\[
\begin{eqnarray}
e_{\mathrm {u}} -e_{\mathrm {v}}&=&\sqrt {2}E \sin \theta -\sqrt {2}E \sin \left( \theta -\frac {2}{3}\pi \right) \\[ 5pt ]
&=&\sqrt {2}E\times 2\cos \left( \theta -\frac {\pi }{3}\right)\sin \frac {\pi}{3} \left( ∵和積の公式\right) \\[ 5pt ]
&=&\sqrt {2}E\times 2\cos \left( \theta -\frac {\pi }{3}\right) \cdot \frac {\sqrt {3}}{2} \\[ 5pt ]
&=&\sqrt {6}E\cos \left( \theta -\frac {\pi }{3}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので平均出力電圧\( \ E_{\mathrm {d}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {d}}&=&\frac {1}{\displaystyle \frac {\pi }{3}}\int _{\frac {\pi }{6}+\alpha }^{\frac {\pi }{2}+\alpha }\sqrt {6}E\cos \left( \theta -\frac {\pi }{3}\right) \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi }\int _{\frac {\pi }{6}+\alpha }^{\frac {\pi }{2}+\alpha }\cos \left( \theta -\frac {\pi }{3}\right) \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi }\left[ \sin \left( \theta -\frac {\pi }{3}\right) \right] _{\frac {\pi }{6}+\alpha }^{\frac {\pi }{2}+\alpha } \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi }\left\{ \sin \left( \alpha +\frac {\pi }{6}\right) -\sin \left( \alpha -\frac {\pi }{6}\right) \right\} \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi } \cdot 2\cos \alpha \sin \frac {\pi }{6} \left( ∵和積の公式\right) \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi } \cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
となります。(和積の公式はこちら)ここで,電源の線間電圧\( \ V \ \)の大きさは相電圧の\( \ \sqrt {3} \ \)倍の大きさなので,
\[
\begin{eqnarray}
E_{\mathrm {d}}&=&\frac {3\sqrt {2}V}{\pi } \cos \alpha \\[ 5pt ]
&≒&1.35V\cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ワ
題意より解答候補は,(ロ)\(1\),(チ)\(\displaystyle \frac {1}{\sqrt {3}}\),(ワ)\(\sqrt {3}\),になると思います。
ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り,\( \ \mathrm {Y} \ \)結線において,線間電圧は相電圧の\( \ \sqrt {3} \ \)倍となるので,\( \ \mathrm {S}_{1} \ \)と\( \ \mathrm {S}_{2} \ \)が同電圧を出力するためには,\( \ \mathrm {S}_{2} \ \)の巻数を\( \ \mathrm {S}_{1} \ \)の\( \ \sqrt {3} \ \)倍にしておく必要があります。
(2)解答:イ
題意より解答候補は,(イ)\(1.35E\cos \alpha \),(ト)\(0.90E\cos \alpha \),(ヲ)\(0.45E\cos \alpha \),になると思います。
ワンポイント解説「3.三相サイリスタブリッジ整流回路の平均出力電圧\( \ E_{\mathrm {d}} \ \)」の通り,各ブリッジの直流電圧の平均値は\( \ 1.35E\cos \alpha \ \)となります。
二次試験では導出できるレベルになる必要がありますが,一次試験においては覚えておいた方が良いと思います。
(3)解答:ヌ
題意より解答候補は,(ニ)\(60°\),(ホ)\(120°\),(ヌ)\(30°\),になると思います。
ワンポイント解説「3.三相サイリスタブリッジ整流回路の平均出力電圧\( \ E_{\mathrm {d}} \ \)」の図8の通り,\( \ \mathrm {S}_{1} \ \)及び\( \ \mathrm {S}_{2} \ \)からは\(60°\left( \displaystyle \frac {\pi }{3}\right) \ \)周期の電圧が出力されますが,ワンポイント解説「1.\( \ \mathrm {Y} \ \)結線における相電圧と線間電圧の関係」の通り,\( \ \mathrm {S}_{1} \ \)の方が\( \ \mathrm {S}_{2} \ \)よりも\(30°\left( \displaystyle \frac {\pi }{6}\right) \ \)進んだ波形となるため,重ね合わせると全体としては\(30°\left( \displaystyle \frac {\pi }{6}\right) \ \)の繰り返し周期となることがわかります。
(4)解答:リ
題意より解答候補は,(リ)\( \left( \mathrm {a}\right) \),(ル)\( \left( \mathrm {b}\right) \),(カ)\( \left( \mathrm {c}\right) \),になると思います。
問題文において,図2は「変圧器二次側の各部の電流\( \ i_{\mathrm {u1}} \ \),\( \ i_{\mathrm {u2}} \ \)及び\( \ i_{\mathrm {uv2}} \ \)の波形を示す」となっており,\( \ i_{\mathrm {u1}} \ \),\( \ i_{\mathrm {u2}} \ \)は同じ形の波形で,ワンポイント解説「2.\( \ \Delta \ \)結線における相電流と線電流の関係」の通り\( \ i_{\mathrm {u2}} \ \)の電流が\( \ i_{\mathrm {u1}} \ \)より遅れた波形となるので,\( \left( \mathrm {a}\right) \)が\( \ i_{\mathrm {u2}} \ \)の波形となります。
(5)解答:ヘ
題意より解答候補は,(ハ)\( \ 5 \ \)次,\( \ 7 \ \)次,\( \ 11 \ \)次,\( \ 13 \ \)次,\( \ \cdots \ \),(ヘ)\( \ 11 \ \)次,\( \ 13 \ \)次,\( \ \cdots \ \),(ヨ)\( \ 3 \ \)次,\( \ 5 \ \)次,\( \ 7 \ \)次,\( \ 11 \ \)次,\( \ 13 \ \)次,\( \ \cdots \ \),になると思います。
一般にパルス数\( \ p \ \)のインバータでの高調波は\( \ kp±1 \left( k=1,2,\cdots \right) \ \)の高調波が発生します。したがって,\( \ 12 \ \)パルスインバータでの高調波電流は,(ヘ)\( \ 11 \ \)次,\( \ 13 \ \)次,\( \ 23 \ \)次,\( \ 25 \ \)次,\( \ \cdots \ \)の高調波が発生することになります。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん