【問題】
【難易度】★☆☆☆☆(易しい)
次の文章は,配電系統における電力用コンデンサに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
a 有効電力\( \ P \ \),力率\( \ \cos \theta _{1} \ \)の負荷がある。この負荷の力率を,\( \ \cos \theta _{2} \ \)に改善するために必要な並列コンデンサの容量は,コンデンサの設置前後で負荷の有効電力が変化しないとするならば,\( \ \fbox { (1) } \ \)であり,このとき,負荷に接続している配電線から供給される皮相電力は,\( \ \fbox { (2) } \ \)だけ減少する。
b 上記aの場合,コンデンサの設置により,配電線の電圧降下は,配電線の抵抗を\( \ R \ \),リアクタンスの\( \ X \ \),コンデンサ電流を\( \ I_{\mathrm {C}} \ \)とすると,配電線両端の電圧位相角が小さいならば,ほぼ\( \ \fbox { (3) } \ \)だけ減少する。
c 配電系統には高周波源が存在するため,コンデンサの電圧波形ひずみが拡大することがある。これは,コンデンサの設置点からみた配電系統のインダクタンスとコンデンサのキャパシタンスが\( \ \fbox { (4) } \ \)の関係となるためであり,この対策として,コンデンサと\( \ \fbox { (5) } \ \)にリアクトルを接続し,合成リアクタンスを高調波に対して誘導性となるようにする。この条件は,コンデンサの基本波リアクタンスに対するリアクトルの基本波リアクタンスの比を\( \ \alpha \ \),高調波次数を\( \ n \ \)とすると,\( \ \fbox { (6) } \ \)である。通常,この比は第5次高調波に対して誘導性となるようにすればよく,\( \ \mathrm {JIS} \ \)では,\( \ \fbox { (7) } \ \)と規定されている。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& 並 列 &(ロ)& P\left( \frac {1}{\sin \theta _{2}}-\frac {1}{\sin \theta _{1}}\right) &(ハ)& 直 列 \\[ 5pt ]
&(ニ)& P\left( \frac {1}{\cos \theta _{1}}-\frac {1}{\cos \theta _{2}}\right) &(ホ)& 発 振 &(ヘ)& 2 \ % \\[ 5pt ]
&(ト)& 共 振 &(チ)& I_{\mathrm {C}}X &(リ)& P\left( \sin \theta _{1}-\sin \theta _{2}\right) \\[ 5pt ]
&(ヌ)& \alpha < \frac {1}{n} &(ル)& P\left( \frac {1}{\tan \theta _{2}}-\frac {1}{\tan \theta _{1}}\right) &(ヲ)& 6 \ % \\[ 5pt ]
&(ワ)& P\left( \cos \theta _{2}-\cos \theta _{1}\right) &(カ)& 4 \ % &(ヨ)& \alpha > \frac {1}{n^{3}} \\[ 5pt ]
&(タ)& I_{\mathrm {C}}\left( R +X\right) &(レ)& \alpha > \frac {1}{n^{2}} &(ソ)& I_{\mathrm {C}}\sqrt {R^{2} +X^{2}} \\[ 5pt ]
&(ツ)& P\left( \tan \theta _{1}-\tan \theta _{2}\right) &(ネ)& 鉄共振
\end{eqnarray}
\]
【ワンポイント解説】
電気施設管理の問題ですが,内容としてはほぼ電力科目の問題で,難易度も二種~三種レベルの問題です。一種では後半の問題の配点が高いので,本問を確実に得点できるかどうかが合否の分かれ目となりそうです。
【解答】
(1)解答:ツ
題意に沿ってベクトル図を描くと図1のようになる。力率が\( \ \cos \theta _{1} \ \)から\( \ \cos \theta _{2} \ \)に変化した時の電力変化量がコンデンサの容量であるから,コンデンサ容量は図1の\( \ Q_{\mathrm {C}} \ \)となる。よって,
\[
\begin{eqnarray}
Q_{\mathrm {C}} &=& Q_{1} – Q_{2} \\[ 5pt ]
&=& P \tan \theta _{1} – P \tan \theta _{2} \\[ 5pt ]
&=& P \left( \tan \theta _{1} – \tan \theta _{2}\right)
\end{eqnarray}
\]
と求められる。

(2)解答:ニ
皮相電力の変化量\( \ \Delta S \ \)は図1の\( \ S_{1} \ \)と\( \ S_{2} \ \)の差であるから,
\[
\begin{eqnarray}
\Delta S &=& S_{1} – S_{2} \\[ 5pt ]
&=& \frac {P}{\cos \theta _{1}}-\frac {P}{\cos \theta _{2}} \\[ 5pt ]
&=& P\left( \frac {1}{\cos \theta _{1}}-\frac {1}{\cos \theta _{2}}\right)
\end{eqnarray}
\]
と求められる。
(3)解答:チ
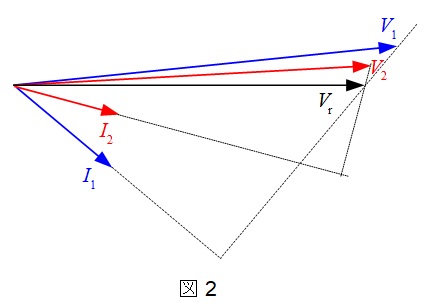
配電線の受電端の電圧を\( \ V_{\mathrm {r}} \ \)とし,力率が\( \ \cos \theta _{1} \ \)の時の送電端電圧を\( \ V_{1} \ \),配電線を流れる電流を\( \ I_{1} \ \)とし,力率が\( \ \cos \theta _{2} \ \)の時の送電端電圧を\( \ V_{2} \ \),配電線を流れる電流を\( \ I_{2} \ \)とし,相差角を十分に小さいとすると,
\[
\begin{eqnarray}
V_{1} &=& V_{\mathrm {r}} + RI_{1}\cos \theta _{1} +X I_{1}\sin \theta _{1} \\[ 5pt ]
V_{2} &=& V_{\mathrm {r}} + RI_{2}\cos \theta _{2} +X I_{2}\sin \theta _{2}
\end{eqnarray}
\]
となるので,電圧降下\( \ v \ \)は,
\[
\begin{eqnarray}
v &=& V_{1}-V_{2} \\[ 5pt ]
&=& \left( V_{\mathrm {r}} + RI_{1}\cos \theta _{1} +X I_{1}\sin \theta _{1}\right) -\left( V_{\mathrm {r}} + RI_{2}\cos \theta _{2} +X I_{2}\sin \theta _{2} \right) \\[ 5pt ]
&≒& X \left( I_{1}\sin \theta _{1}-I_{2}\sin \theta _{2} \right)
\end{eqnarray}
\]
となる。\(I_{\mathrm {C}}=I_{1}\sin \theta _{1}-I_{2}\sin \theta _{2}\)であるから,電圧降下は\(v=I_{\mathrm {C}}X\)となる。
(4)解答:ト
題意より解答候補は(ホ)発振,(ト)共振,(ネ)鉄共振,となりますが,インダクタンスとキャパシタンスで発生するのは共振となります。
(5)解答:ハ
合成リアクタンスを誘導性とするためには,コンデンサとは直列にリアクトルを設置する必要があります。並列に接続しても意味がありません。
(6)解答:レ
基本波のリアクトルのリアクタンスを\( \ X_{\mathrm {L}} \ \),コンデンサのリアクタンスを\( \ X_{\mathrm {C}} \ \)とすると,第\(n\)調波のリアクタンスはそれぞれ\( \ nX_{\mathrm {L}} \ \),\( \ \displaystyle \frac {1}{n}X_{\mathrm {C}} \ \)となるので,合成リアクタンスは誘導性になるためには,
\[
\begin{eqnarray}
nX_{\mathrm {L}} &>& \frac {1}{n}X_{\mathrm {C}} \\[ 5pt ]
\frac {X_{\mathrm {L}}}{X_{\mathrm {C}}} &>& \frac {1}{n^{2}} \\[ 5pt ]
\alpha &>& \frac {1}{n^{2}}
\end{eqnarray}
\]
となる必要がある。
(7)解答:ヲ
(6)解答式に\( \ n=5 \ \)を代入すると,
\[
\begin{eqnarray}
\alpha &>& \frac {1}{5^{2}} \\[ 5pt ]
\alpha &>& 0.04
\end{eqnarray}
\]
となり,理論的には4%より大きくなればよいですが,\( \ \mathrm {JIS} \ \)では6%と規定されています。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん