【問題】
【難易度】★★★★★(難しい)
次の文章は,同期機のリアクタンス測定法に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。なお,電機子巻線抵抗などの抵抗分は無視する。また,電圧の単位は\( \ [ \ \mathrm {V} \ ] \ \),電流の単位は\( \ [ \ \mathrm {A} \ ] \ \),リアクタンスの単位は\( \ [ \ \Omega \ ] \ \)である。
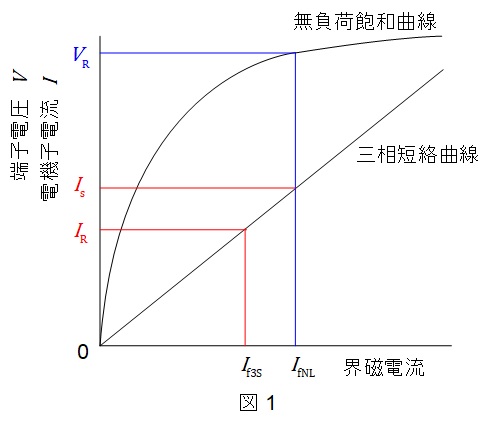
a 直軸同期リアクタンス\( \ X_{\mathrm {d}} \ \)の代表的な測定法として,無負荷飽和特性曲線及び三相短絡電流特性曲線から求める方法がある。この方法では,無負荷飽和特性曲線上の電機子定格電圧(線間電圧)\( \ V_{\mathrm {R}} \ \)を誘起するのに要する\( \ I_{\mathrm {fNL}} \ \)及び三相短絡電流特性曲線上の電機子定格電流(相電流)\( \ I_{\mathrm {R}} \ \)を流すのに要する界磁電流\( \ I_{\mathrm {f3S}} \ \)を用いて,\( \ X_{\mathrm {d}}= \ \fbox { (1) } \ \)の式によって計算される。
b 直軸同期リアクタンス及び横軸同期リアクタンスの測定法の一つに滑り法がある。この方法では,界磁回路を開放し,無励磁のまま回転子を駆動機によって\( \ \fbox { (2) } \ \)速度で回転させ,電機子回路に定格周波数の三相対称低電圧(電機子定格電圧の\( \ 10 \ % \ \)程度)を加える。このときの電機子端子電圧(線間電圧)及び電機子電流(相電流)を記録し,電機子端子電圧の最大値\( \ V_{\max} \ \),最小値\( \ V_{\min} \ \)及び電機子電流の最大値\( \ I_{\max} \ \),最小値\( \ I_{\min} \ \)を求める。これらの測定値から滑り法による直軸同期リアクタンス\( \ X_{\mathrm {sd}} \ \)は,\( \ \displaystyle X_{\mathrm {sd}}=\frac {V_{\max}}{\sqrt {3}I_{\min}} \ \)によって,滑り法による横軸同期リアクタンス\( \ X_{\mathrm {sq}} \ \)は,\( \ \displaystyle X_{\mathrm {sq}}=\frac {V_{\min}}{\sqrt {3}I_{\max}} \ \)によって求めることができる。また,横軸同期リアクタンス\( \ X_{\mathrm {q}} \ \)は,a項で求めた\( \ X_{\mathrm {d}} \ \)を用い,\( \ X_{\mathrm {q}}= \ \fbox { (3) } \ \)の式によってa項の\( \ X_{\mathrm {d}} \ \)の数値に整合する数値が得られる。
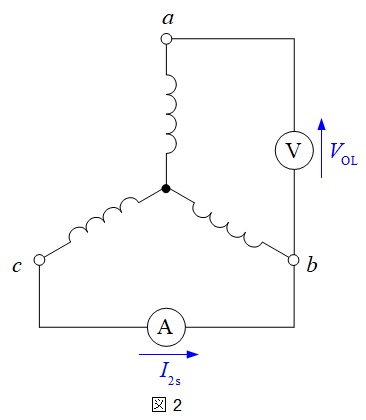
c 逆相リアクタンス\( \ X_{2} \ \)の測定法として単相短絡法がある。この方法では,電機子巻線の2端子を短絡し,短絡回路には電流計,短絡回路と開放端子との間には電圧計を接続し,同期機を定格回転速度で運転する。界磁電流を流して,短絡電機子回路電流\( \ I_{\mathrm {2s}} \ \)及び短絡回路と開放端子との間の線間電圧\( \ V_{\mathrm {OL}} \ \)を測定し,\( \ X_{2}= \ \fbox { (4) } \ \)の式によって計算される。
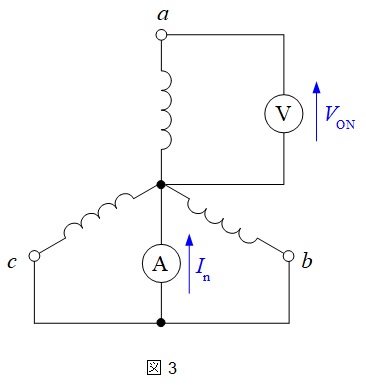
d 零相リアクタンス\( \ X_{0} \ \)の測定法として二相接地法がある。この方法では,電機子巻線の短絡した2端子と中性点間とを更に短絡し,その短絡した2端子と中性点の間に電流計,開放端子と中性点の間には電圧計を接続し,同期機を定格回転速度で運転する。界磁電流を流して,中性点電流\( \ I_{\mathrm {n}} \ \)及び相電圧\( \ V_{\mathrm {ON}} \ \)を測定し,\( \ X_{0}= \ \fbox { (5) } \ \)の式によって計算される。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {V_{\mathrm {ON}}}{3I_{\mathrm {n}}} &(ロ)& \frac {V_{\mathrm {R}}I_{\mathrm {f3S}}}{\sqrt {3}I_{\mathrm {R}}I_{\mathrm {fNL}}} &(ハ)& \frac {V_{\mathrm {R}}I_{\mathrm {fNL}}}{\sqrt {3}I_{\mathrm {R}}I_{\mathrm {f3S}}} \\[ 5pt ]
&(ニ)& X_{\mathrm {d}}\frac {V_{\min}I_{\min}}{V_{\max}I_{\max}} &(ホ)& \frac {V_{\mathrm {OL}}}{3I_{\mathrm {2s}}} &(ヘ)& \frac {V_{\mathrm {OL}}}{\sqrt {3}I_{\mathrm {2s}}} \\[ 5pt ]
&(ト)& 同 期 &(チ)& 同期速度から僅かに外れた &(リ)& \frac {I_{\mathrm {f3S}}}{I_{\mathrm {fNL}}} \\[ 5pt ]
&(ヌ)& \frac {3V_{\mathrm {OL}}}{I_{\mathrm {2s}}} &(ル)& \frac {3V_{\mathrm {ON}}}{I_{\mathrm {n}}} &(ヲ)& X_{\mathrm {d}}\frac {V_{\max}I_{\max}}{V_{\min}I_{\min}} \\[ 5pt ]
&(ワ)& 定格回転 &(カ)& X_{\mathrm {d}}\frac {V_{\max}I_{\min}}{V_{\min}I_{\max}} &(ヨ)& \frac {V_{\mathrm {ON}}}{I_{\mathrm {n}}}
\end{eqnarray}
\]
【ワンポイント解説】
(1)~(3)までは標準的な内容ですが,(4),(5)については対称座標法にて連立方程式を解く必要があり,非常に難しい問題と言えます。
1.電動機の特性曲線
電動機は図1のような無負荷飽和特性曲線と三相短絡電流特性があります。直軸同期リアクタンス\( \ X_{\mathrm {d}} \ \)は図1の\( \ \displaystyle \frac {V_{\mathrm {R}} / \sqrt{3}}{I_{\mathrm {s}}} \ \)で求められます。
2.滑り法による直軸同期リアクタンス及び横軸同期リアクタンスの測定法
界磁回路を開放し,無励磁のまま回転子を駆動機によって同期速度から僅かに外れた速度(\( \ 1.0 \ % \ \)以内)で回転させ,電機子回路に定格周波数の三相対称定電圧(電機子定格電圧の\( \ 10 \ % \ \)程度)を加えます。このときの電機子端子電圧(線間電圧)及び電機子電流(相電流)を記録し,電機子端子電圧の最大値\( \ V_{\max} \ \),最小値\( \ V_{\min} \ \)及び電機子電流の最大値\( \ I_{\max} \ \),最小値\( \ I_{\min} \ \)を求め,直軸同期リアクタンス\( \ X_{\mathrm {sd}} \ \)は,\( \ \displaystyle X_{\mathrm {sd}}=\frac {V_{\max}}{\sqrt {3}I_{\min}} \ \),横軸同期リアクタンス\( \ X_{\mathrm {sq}} \ \)は,\( \ \displaystyle X_{\mathrm {sq}}=\frac {V_{\min}}{\sqrt {3}I_{\max}} \ \)によって求めることができます。
3.単相短絡法
逆相リアクタンス\( \ X_{2} \ \)を求める測定法で,図2のように電機子巻線の2端子を短絡し,短絡回路には電流計,短絡回路と開放端子との間には電圧計を接続し,同期機を定格回転速度で運転します。界磁電流を流して,短絡電機子回路電流\( \ I_{\mathrm {2s}} \ \)及び短絡回路と開放端子との間の線間電圧\( \ V_{\mathrm {OL}} \ \)を測定し,逆相リアクタンス\( \ X_{2} \ \)を求めます。
4.二相接地法
零相リアクタンス\( \ X_{0} \ \)を求める測定法で,図3のように電機子巻線の短絡した2端子と中性点間とを更に短絡し,その短絡した2端子と中性点の間に電流計,開放端子と中性点の間には電圧計を接続し,同期機を定格回転速度で運転し,界磁電流を流して,中性点電流\( \ I_{\mathrm {a}} \ \)及び相電圧\( \ V_{\mathrm {ON}} \ \)を測定し,零相リアクタンス\( \ X_{0} \ \)を求めます。
5.対称座標法
零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \)とすると,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2}
\end{eqnarray}
\]
零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}
\end{eqnarray}
\]
また,対称座標法における発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-Z_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-Z_{2}{\dot I}_{2}
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)解答:ロ
図1より,
\[
\begin{eqnarray}
\frac {I_{\mathrm {R}}}{I_{\mathrm {s}}} &=&\frac {I_{\mathrm {f3S}}}{I_{\mathrm {fNL}}} \\[ 5pt ]
I_{\mathrm {s}}&=& \frac {I_{\mathrm {R}}I_{\mathrm {fNL}}}{I_{\mathrm {f3S}}}
\end{eqnarray}
\]
であり,\( \ X_{\mathrm {d}}=\displaystyle \frac {V_{\mathrm {R}}/ \sqrt{3}}{I_{\mathrm {s}}} \ \)であるから,
\[
\begin{eqnarray}
X_{\mathrm {d}} &=&\frac {V_{\mathrm {R}}/ \sqrt{3}}{I_{\mathrm {s}}} \\[ 5pt ]
&=& \frac {V_{\mathrm {R}}I_{\mathrm {f3S}}}{\sqrt {3}I_{\mathrm {R}}I_{\mathrm {fNL}}}
\end{eqnarray}
\]
と求められる。
(2)解答:チ
ワンポイント解説「2.滑り法による直軸同期リアクタンス及び横軸同期リアクタンスの測定法」の通り,同期速度から僅かに外れた速度で上下させながら測定します。
(3)解答:ニ
\[
\begin{eqnarray}
\frac {X_{\mathrm {sq}}}{X_{\mathrm {sd}}} &=&\frac {X_{\mathrm {q}}}{X_{\mathrm {d}}} \\[ 5pt ]
X_{\mathrm {q}}&=& X_{\mathrm {d}} \frac {X_{\mathrm {sq}}}{X_{\mathrm {sd}}}
\end{eqnarray}
\]
の関係があるから,題意より,\( \ \displaystyle X_{\mathrm {sd}}=\frac {V_{\max}}{\sqrt {3}I_{\min}} \ \),\( \ \displaystyle X_{\mathrm {sq}}=\frac {V_{\min}}{\sqrt {3}I_{\max}} \ \)を代入すると,
\[
\begin{eqnarray}
X_{\mathrm {q}}&=& X_{\mathrm {d}} \frac {\displaystyle \frac {V_{\min}}{\sqrt {3}I_{\max}}}{\displaystyle \frac {V_{\max}}{\sqrt {3}I_{\min}}} \\[ 5pt ]
X_{\mathrm {q}}&=& X_{\mathrm {d}}\frac {V_{\min}I_{\min}}{V_{\max}I_{\max}}
\end{eqnarray}
\]
と求められる。
(4)解答:ヘ
図2の単相短絡法において,
\[
\begin{eqnarray}
V_{\mathrm {OL}} &=& \left| {\dot V}_{\mathrm {a}} -{\dot V}_{\mathrm {b}}\right| \\[ 5pt ]
I_{\mathrm {2s}} &=& \left| {\dot I}_{\mathrm {c}}\right| = \left| -{\dot I}_{\mathrm {b}}\right| \\[ 5pt ]
\end{eqnarray}
\]
である。また,ワンポイント解説「5.対称座標法」より
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} &・・・①& \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} &・・・②& \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} = {\dot V}_{\mathrm {b}} &・・・③& \\[ 5pt ]
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} =0 &・・・④&\\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} &・・・⑤& \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} =-{\dot I}_{\mathrm {b}} &・・・⑥& \\[ 5pt ]
{\dot V}_{0} &=&-Z_{0}{\dot I}_{0} &・・・⑦& \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} &・・・⑧& \\[ 5pt ]
{\dot V}_{2} &=&-Z_{2}{\dot I}_{2} &・・・⑨&
\end{eqnarray}
\]
となる。\(②\),\(③\)より,
\[
\begin{eqnarray}
{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} &=& {\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\left( a^{2}-a \right) {\dot V}_{1}&=& \left( a^{2}-a \right) {\dot V}_{2} \\[ 5pt ]
{\dot V}_{1}&=&{\dot V}_{2} ・・・⑩
\end{eqnarray}
\]
となる。また\(④+⑤+⑥\)より,
\[
\begin{eqnarray}
3{\dot I}_{0} &=& {\dot I}_{\mathrm {a}}+ {\dot I}_{\mathrm {b}} + {\dot I}_{\mathrm {c}} \\[ 5pt ]
&=& 0+ {\dot I}_{\mathrm {b}} – {\dot I}_{\mathrm {b}} \\[ 5pt ]
{\dot I}_{0} &=& 0 ・・・⑪
\end{eqnarray}
\]
となる。\(⑤\),\(⑥\),\(⑪\)より,
\[
\begin{eqnarray}
a{\dot I}_{1} + a^{2}{\dot I}_{2} &=& -\left( a^{2}{\dot I}_{1} + a{\dot I}_{2}\right) \\[ 5pt ]
\left(a +a^{2}\right) {\dot I}_{1} &=&-\left(a +a^{2}\right) {\dot I}_{2} \\[ 5pt ]
{\dot I}_{1} &=& -{\dot I}_{2} ・・・⑫
\end{eqnarray}
\]
となるので,\(⑩\),\(⑫\)より\(⑧\)は,
\[
{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} = -Z_{2}{\dot I}_{2} = Z_{2}{\dot I}_{1}
\]
となるので,これより,
\[
\begin{eqnarray}
{\dot I}_{1}=-{\dot I}_{2}&=&\frac {{\dot E}_{\mathrm {a}}}{Z_{1}+Z_{2}} \\[ 5pt ]
{\dot V}_{1}={\dot V}_{2}&=&\frac {Z_{2}{\dot E}_{\mathrm {a}}}{Z_{1}+Z_{2}}
\end{eqnarray}
\]
と求めることができる。これらより,\( \ V_{\mathrm {OL}} \ \),\( \ I_{\mathrm {2s}} \ \)は
\[
\begin{eqnarray}
V_{\mathrm {OL}} &=& \left| {\dot V}_{\mathrm {a}} -{\dot V}_{\mathrm {b}}\right| \\[ 5pt ]
&=& \left| \left(1-a^{2}\right) {\dot V}_{\mathrm {1}} +\left(1-a\right) {\dot V}_{\mathrm {2}}\right| \\[ 5pt ]
&=& \left| \left(2-a^{2}-a\right) {\dot V}_{\mathrm {1}}\right| \\[ 5pt ]
&=& \left| 3 {\dot V}_{\mathrm {1}}\right| \\[ 5pt ]
&=& \frac {3Z_{2}{\dot E}_{\mathrm {a}}}{Z_{1}+Z_{2}} \\[ 5pt ]
I_{\mathrm {2s}} &=& \left| {\dot I}_{\mathrm {c}}\right| \\[ 5pt ]
&=& \left| {\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}\right| \\[ 5pt ]
&=& \left| \left( a-a^{2}\right) {\dot I}_{1} \right| \\[ 5pt ]
&=& \left| \mathrm {j}\sqrt {3} {\dot I}_{1} \right| \\[ 5pt ]
&=& \left| \mathrm {j}\sqrt {3} \frac {{\dot E}_{\mathrm {a}}}{Z_{1}+Z_{2}} \right| \\[ 5pt ]
&=& \frac {\sqrt {3}{\dot E}_{\mathrm {a}}}{Z_{1}+Z_{2}}
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\frac {V_{\mathrm {OL}}}{I_{\mathrm {2s}}}&=&\frac {\displaystyle \frac {3Z_{2}{\dot E}_{\mathrm {a}}}{Z_{1}+Z_{2}}}{\displaystyle \frac {\sqrt {3}{\dot E}_{\mathrm {a}}}{Z_{1}+Z_{2}}} \\[ 5pt ]
&=&\sqrt {3}Z_{2} \\[ 5pt ]
Z_{2}&=&\frac {V_{\mathrm {OL}}}{\sqrt {3}I_{\mathrm {2s}}}
\end{eqnarray}
\]
と求められる。
(5)解答:ヨ
\[
\begin{eqnarray}
V_{\mathrm {ON}} &=& \left| {\dot V}_{\mathrm {a}} \right| \\[ 5pt ]
I_{\mathrm {n}} &=& \left| {\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}}\right|
\end{eqnarray}
\]
である。また,ワンポイント解説「5.対称座標法」より
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} &・・・①^{\prime }& \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} =0 &・・・②^{\prime }& \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} = 0 &・・・③^{\prime }& \\[ 5pt ]
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} =0 &・・・④^{\prime }&\\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} &・・・⑤^{\prime }& \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} &・・・⑥^{\prime }& \\[ 5pt ]
{\dot V}_{0} &=&-Z_{0}{\dot I}_{0} &・・・⑦^{\prime }& \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} &・・・⑧^{\prime }& \\[ 5pt ]
{\dot V}_{2} &=&-Z_{2}{\dot I}_{2} &・・・⑨^{\prime }&
\end{eqnarray}
\]
となる。\(②^{\prime }\),\(③^{\prime }\)に\(⑦^{\prime }\),\(⑧^{\prime }\),\(⑨^{\prime }\)を代入すると,
\[
\begin{eqnarray}
-Z_{0}{\dot I}_{0}+ a\left( {\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1}\right) – a^{2}Z_{2}{\dot I}_{2} &=& 0 &・・・⑩^{\prime }&\\[ 5pt ]
-Z_{0}{\dot I}_{0}+ a^{2}\left( {\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1}\right) – aZ_{2}{\dot I}_{2} &=& 0 &・・・⑪^{\prime }&
\end{eqnarray}
\]
となる。\(⑩^{\prime }\times a -⑪^{\prime }\)より,
\[
\begin{eqnarray}
\left( 1-a\right) Z_{0}{\dot I}_{0}- \left( 1-a\right)Z_{2}{\dot I}_{2} &=& 0 \\[ 5pt ]
{\dot I}_{2} &=& \frac {Z_{0}}{Z_{2}}{\dot I}_{0}
\end{eqnarray}
\]
となり,\(⑩^{\prime } -⑪^{\prime }\times a\)より,
\[
\begin{eqnarray}
\left( a-1\right) Z_{0}{\dot I}_{0} +\left( a-1\right)\left( {\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1}\right) &=& 0 \\[ 5pt ]
Z_{0}{\dot I}_{0} + {\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1}&=& 0 \\[ 5pt ]
{\dot I}_{1}&=& \frac {1}{Z_{1}}\left( {\dot E}_{\mathrm {a}}+ Z_{0}{\dot I}_{0}\right)
\end{eqnarray}
\]
となるので,これらを\(④^{\prime }\)に代入すると,
\[
\begin{eqnarray}
{\dot I}_{0}+ \frac {1}{Z_{1}}\left( {\dot E}_{\mathrm {a}}+ Z_{0}{\dot I}_{0}\right) + \frac {Z_{0}}{Z_{2}}{\dot I}_{0} &=&0 \\[ 5pt ]
{\dot I}_{0}&=& -\frac {{\dot E}_{\mathrm {a}}}{Z_{1}}\frac {1}{\displaystyle 1+\frac {Z_{0}}{Z_{1}}+\frac {Z_{0}}{Z_{2}}}
\end{eqnarray}
\]
となり,これを発電機の基本式に代入すれば,
\[
{\dot V}_{0}={\dot V}_{1}={\dot V}_{2}=\frac {Z_{0}{\dot E}_{\mathrm {a}}}{Z_{1}}\frac {1}{\displaystyle 1+\frac {Z_{0}}{Z_{1}}+\frac {Z_{0}}{Z_{2}}}
\]
と求められる。よって,\( \ V_{\mathrm {ON}} \ \)と\( \ I_{\mathrm {n}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {ON}} &=& \left| {\dot V}_{\mathrm {a}} \right| \\[ 5pt ]
&=& \left| {\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \right| \\[ 5pt ]
&=& \left| 3{\dot V}_{0} \right| \\[ 5pt ]
&=& \frac {3Z_{0}{\dot E}_{\mathrm {a}}}{Z_{1}}\frac {1}{\displaystyle 1+\frac {Z_{0}}{Z_{1}}+\frac {Z_{0}}{Z_{2}}} \\[ 5pt ]
I_{\mathrm {n}} &=& \left| {\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}}\right| \\[ 5pt ]
&=& \left| {\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2}+{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}\right| \\[ 5pt ]
&=& \left| 2{\dot I}_{0}-{\dot I}_{1} -{\dot I}_{2}\right| \\[ 5pt ]
&=& \left| 3{\dot I}_{0}-\left( {\dot I}_{0}+{\dot I}_{1} +{\dot I}_{2}\right) \right| \\[ 5pt ]
&=& \left| 3{\dot I}_{0} \right| \\[ 5pt ]
&=& \left| -\frac {3{\dot E}_{\mathrm {a}}}{Z_{1}}\frac {1}{\displaystyle 1+\frac {Z_{0}}{Z_{1}}+\frac {Z_{0}}{Z_{2}}} \right| \\[ 5pt ]
&=& \frac {3{\dot E}_{\mathrm {a}}}{Z_{1}}\frac {1}{\displaystyle 1+\frac {Z_{0}}{Z_{1}}+\frac {Z_{0}}{Z_{2}}}
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\frac {V_{\mathrm {ON}}}{I_{\mathrm {n}}}&=&\frac {\displaystyle \frac {3Z_{0}{\dot E}_{\mathrm {a}}}{Z_{1}}\frac {1}{\displaystyle 1+\frac {Z_{0}}{Z_{1}}+\frac {Z_{0}}{Z_{2}}}}{\displaystyle \frac {3{\dot E}_{\mathrm {a}}}{Z_{1}}\frac {1}{\displaystyle 1+\frac {Z_{0}}{Z_{1}}+\frac {Z_{0}}{Z_{2}}} } \\[ 5pt ]
Z_{0}&=& \frac {V_{\mathrm {ON}}}{I_{\mathrm {n}}}
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん