《機械》〈パワーエレクトロニクス〉[H28:問3] 高周波インバータに関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，高周波インバータに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

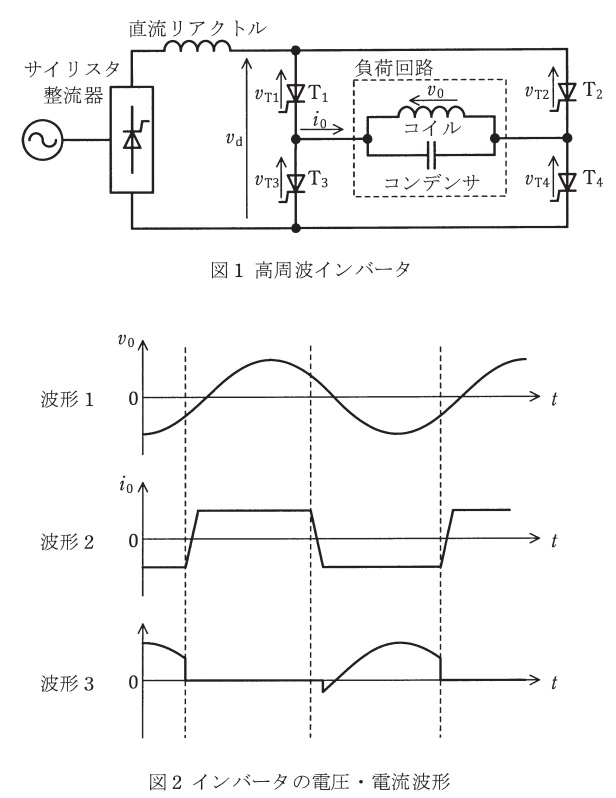
図1には誘導加熱用などに使われる高周波インバータの定常運転に関与する主回路部分だけを示す。サイリスタ整流器は交流入力を整流し，十分に大きなインダクタンス$ \ \mathrm{L_{d}} \ $をもつ直流リアクトルによってほぼ一定の直流電流を得る。インバータはこの電流を交流に変換して負荷に供給し，その運転周波数は$ \ \mathrm {500 \ Hz \ ～ \ 10 \ kHz} \ $程度であることが一般的である。

高周波インバータの主な負荷はコイルであり，その中に金属部品などの材料を挿入して，高周波の誘導電流で材料にエネルギーを与えて加熱する。したがって，コイルは等価的にリアクトル$ \ \mathrm{L} \ $と抵抗$ \ \mathrm{R} \ $が並列接続された力率の非常に低い誘導性インピーダンスとみなせる。$ \ \mathrm{L} \ $による$ \ \fbox {　（１）　} \ $を補償するために，コンデンサ$ \ \mathrm{C} \ $を設けて並列共振回路を構成した例が図1である。コイルとコンデンサを合わせてインバータの負荷回路とし，その共振回路の先鋭度を$ \ Q \ $とする。インバータの運転中は，インバータ出力電流の基本波振幅に比べほぼ$ \ \fbox {　（２）　} \ $の振幅の循環電流がコイルとコンデンサの間に流れるが，インバータの出力電流は，コイル電流とコンデンサ電流の差分となり，等価的な$ \ \mathrm{R} \ $を流れる電流成分にほぼ相当する。

インバータのサイリスタを転流する際には負荷電圧を利用している。例として，それまで通電していたサイリスタ$ \ \mathrm{T_{1}} \ $，$ \ \mathrm{T_{4}} \ $をターンオフすることを考える。図1に示した出力電圧$ \ v_{0} \ $の方向を正とすると，サイリスタ$ \ \mathrm{T_{2}} \ $，$ \ \mathrm{T_{3}} \ $をオンするときに，コンデンサは$ \ \fbox {　（３）　} \ $に充電されていなければならない。この結果，インバータの出力電圧$v_{0}$と出力電流$i_{0}$は図2に示す波形1と波形2になる。共振回路の先鋭度が高いと，出力電圧$ \ v_{0} \ $はより正弦波に近い電圧波形となる。図2の波形3は電圧$ \ \fbox {　（４）　} \ $の波形である。サイリスタは，インバータの出力電圧波形の定められた位相でスイッチングすることによって安定な動作が実現する。以上から，インバータは，$ \ \mathrm{L} \ $と$ \ \mathrm{C} \ $の並列共振周波数$ \ \fbox {　（５）　} \ $周波数で運転を続けることになる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　に近い　&（ロ）&　正の電圧　&（ハ）&　直流電圧 \ v_{\mathrm {d}} \ の波高値より大きい負の電圧 \\[ 5pt ] &（ニ）&　Q \ 倍　&（ホ）&　v_{\mathrm {T1}}，v_{\mathrm {T4}}　　　&（ヘ）&　の \ 2 \ 倍の周波数に近い \\[ 5pt ] &（ト）&　v_{\mathrm {T2}}，v_{\mathrm {T3}}　　　&（チ）&　無効電力　&（リ）&　直流電圧 \ v_{\mathrm {d}} \ の波高値より小さい負の電圧 \\[ 5pt ] &（ヌ）&　有効電力　&（ル）&　\frac {1}{Q} \ 倍　&（ヲ）&　の半分の周波数に近い \\[ 5pt ] &（ワ）&　v_{\mathrm {d}}　&（カ）&　2Q \ 倍　&（ヨ）&　電力損失
\end{eqnarray}
\]

【ワンポイント解説】

インバータは直流を交流に変換するものです。メカニズムは問題図の$ \ v_{\mathrm {T1}}，v_{\mathrm {T4}} \ $と$ \ v_{\mathrm {T2}}，v_{\mathrm {T3}} \ $のオンとオフを繰り返し，元々直流だったものを出力電圧$ \ v_{0} \ $と出力電流$ \ i_{0} \ $で交流で取り出します。リアクトルがないと，出力電圧は方形波になってしまいます。

【解答】

(1)解答：チ
題意より解答候補は，（チ）無効電力，（ヌ）有効電力，（ヨ）電力損失，となりますが，リアクトルは無効電力を消費するため，コンデンサで補償します。

(2)解答：ニ
題意より解答候補は，（ニ）$ \ Q \ $倍，（ル）$ \ \displaystyle \frac {1}{Q} \ $倍，（カ）$ \ 2Q \ $倍，となります。
題意で与えられている先鋭度$ \ Q \ $は，共振角周波数を$ \ \omega _{0} \ $とすると，
\[
Q=\frac {R}{\omega _{0}L}
\] となる。リアクトルに流れる無効横流を$ \ i \ $とすると，
\[
i=\frac {v_{0}}{\mathrm {j}\omega _{0}L}
\] となります。一方，出力電流$ \ i_{0} \ $は，
\[
i_{0}=\frac {v_{0}}{R}
\] となるので，出力電流$ \ i_{0} \ $と循環電流$ \ i \ $の比は，
\[
\begin{eqnarray}
\left| \frac {i}{i_{0}}\right| &=& \left| \frac {\displaystyle \frac {v_{0}}{\mathrm {j}\omega _{0}L}}{\displaystyle \frac {v_{0}}{R}}\right| \\[ 5pt ] &=& \frac {R}{\omega _{0}L} \\[ 5pt ] &=& Q
\end{eqnarray}
\] となります。

(3)解答：ロ
題意より解答候補は，（ロ）正の電圧，（ハ）直流電圧$ \ v_{\mathrm {d}} \ $の波高値より大きい負の電圧，（リ）直流電圧$ \ v_{\mathrm {d}} \ $の波高値より小さい負の電圧，となります。$ \ v_{\mathrm {T1}}，v_{\mathrm {T4}} \ $から$ \ v_{\mathrm {T2}}，v_{\mathrm {T3}} \ $に切り替わる時，$ \ i_{0} \ $はすぐ切り替わりますが，コンデンサには$ \ v_{\mathrm {T1}}，v_{\mathrm {T4}} \ $側からの電圧が充電されている状況でなければなりません。よって，解答は（ロ）正の電圧となります。

(4)解答：ホ
題意より解答候補は，（ホ）$ \ v_{\mathrm {T1}}，v_{\mathrm {T4}} \ $，（ト）$ \ v_{\mathrm {T2}}，v_{\mathrm {T3}} \ $，（ワ）$ \ v_{\mathrm {d}} \ $となりますが，$ \ i_{0} \ $が正のとき$ \ 0 \ $(ON状態)，$ \ i_{0} \ $が負のとき$ \ v_{0} \ $を反転した電圧が発生している(OFF状態)であると考えられます。$ \ i_{0} \ $が正のときONとなり，$ \ i_{0} \ $が負のときOFFとなるのは（ホ）$ \ v_{\mathrm {T1}}，v_{\mathrm {T4}} \ $となります。

(5)解答：イ
題意より解答候補は，（イ）に近い，（ヘ）の2倍の周波数に近い，（ヲ）の半分の周波数に近い，となります。電源側から見た回路にインピーダンスは共振周波数の時最小となるため，サイリスタも共振周波数とほぼ同じタイミングでスイッチオンオフを繰り返します。よって，解答は（イ）に近いとなります。