《機械》〈電気化学〉[R02:問6]燃料電池の特徴及び電解質に関する空欄穴埋問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，燃料電池に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

燃料電池は水素やアルコールなどの燃料をアノードで電気化学的に\( \ \fbox {　 （１） 　} \ \)し，取り出した電子を，外部回路を通じてカソードに供給し，カソードでの反応に用いる。反応の過程で化学エネルギーを直接電気エネルギーに変換するため熱機関のような\( \ \fbox {　 （２） 　} \ \)の制約を受けない。

電解質に\( \ \fbox {　 （３） 　} \ \)を用いる燃料電池を固体高分子形燃料電池をいい，燃料電池自動車や家庭用コジェネレーションシステムで実用化されている。家庭用コジェネレーションシステムの発電効率が\( \ 40 \ \mathrm {％} \ \)であるとすると，発熱量\( \ 45 \ \mathrm {MJ/Nm^{3}} \)の燃料の体積\( \ 1 \ \mathrm {Nm^{3}} \)から\( \ \fbox {　 （４） 　} \ \mathrm {kW\cdot h} \ \)の電力が得られる。電力と熱として利用できる全エネルギーの，燃料の持つ化学エネルギーに対する割合である総合効率が\( \ 97 \ \mathrm {％} \ \)で，燃料電池から得られる熱を用いて\( \ 20 \ \mathrm {℃} \ \)の水を加熱する場合，\( \ \fbox {　 （５） 　} \ \mathrm {L} \ \)の\( \ 60 \ \mathrm {℃} \ \)の温水が得られる。

ただし，水の比熱容量は\( \ 4.18\times 10^{3} \ \mathrm {J\cdot {kg}^{-1}\cdot K^{-1}} \ \)，比重は\( \ 1000 \ \mathrm {kg\cdot m^{-3}} \ \)とする。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　テフロン膜　　　　　&（ロ）&　還元　　　　　&（ハ）&　エネルギー保存則 \\[ 5pt ] &（ニ）&　イオン交換膜　　　　　&（ホ）&　15.3　　　　　&（ヘ）&　10 \\[ 5pt ] &（ト）&　1　　　　　&（チ）&　中和　　　　　&（リ）&　5 \\[ 5pt ] &（ヌ）&　76.5　　　　　&（ル）&　ファラデー効率　　　　　　&（ヲ）&　153 \\[ 5pt ] &（ワ）&　ポリスルフォン膜　　　　　　&（カ）&　カルノー効率　　　　　&（ヨ）&　酸化 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

燃料電池に関する問題です。
燃料電池の仕組みから電解質さらに計算問題まで盛りだくさんな問題ですが，全体的に難易度は高くないため，合格のためにはできれば４箇所以上正答したい問題と言えます。
固体高分子形燃料電池は電気自動車の普及への期待から今後も類題が出題される可能性が大いにあります。確実に理解しておきましょう。

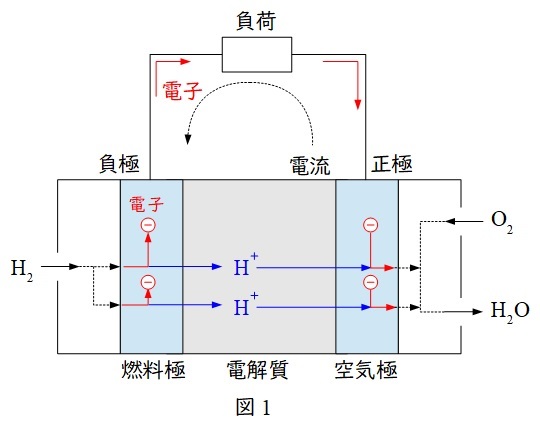
1.燃料電池の概念図
燃料電池は燃料極（負極またはアノードとも言います）に燃料として水素，空気極（正極またはカソードとも言います）に酸素を供給して，化学変化から電気エネルギーを取り出す方法で，正極と負極では以下の反応があります。
負極では水素が電子を失う酸化反応，正極では酸素が電子を受け取る還元反応が起こります。
\[
\begin{eqnarray}
負極&：&\mathrm {H_{2} → 2H^{+} +2e^{-}} \\[ 5pt ] 正極&：&\mathrm {\frac {1}{2}O_{2} + 2H^{+} +2e^{-} →H_{2}O} \\[ 5pt ] \hline
全体&：&\mathrm {H_{2}+\frac {1}{2}O_{2} →H_{2}O}
\end{eqnarray}
\]

2.代表的な燃料電池
電験で扱う燃料電池の主な電解質は以下の通りです。低温形と高温形があり，一般に高温形の方が効率がよく，出力も大きくできるという特徴があります。
①固体高分子形
　電解質：固体高分子膜（イオン交換膜）
　温　度：80～100℃
　出　力：～数百kW
　効　率：30～40%
　用　途：家庭用，自動車用

②リン酸形
　電解質：リン酸
　温　度：150～200℃
　出　力：～数千kW
　効　率：35～45%
　用　途：産業用

③固体酸化物形
　電解質：酸化ジルコニウム（安定化ジルコニア）
　温　度：900～1000℃
　出　力：～数十万kW
　効　率：40～65%
　用　途：分散型電源

④溶融炭酸塩形
　電解質：炭酸塩
　温　度：600～700℃
　出　力：～数十万kW
　効　率：40～60%
　用　途：分散型電源

3.熱量と電力量の関係
\( \ 1 \ \mathrm {kW\cdot h} \ \)は\( \ 1 \ \mathrm {kW} \ \)の電力で\( \ 1 \ \)時間運転した時の電力量です。
また，\( \ 1 \ \mathrm {[W\cdot s]}=1 \ \mathrm {[J]} \ \)の関係があります。したがって，
\[
\begin{eqnarray}
1 \ \mathrm {[kW\cdot h]}&=&3600 \ \mathrm {[kW\cdot s]} \\[ 5pt ] &=&3600 \ \mathrm {[kJ]} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

4.水の温度上昇\( \ \Delta T \ \)と熱量\( \ Q \ \)の関係
温める水の量を\( \ W \ \mathrm {[m^{3}]} \ \)，水の比熱を\( \ c \ \mathrm {[kJ／\left( kg\cdot K\right) ]} \ \)，水の比重を\( \ \rho \ \mathrm {[kg／m^{3}]} \ \)とするとき，水の温度上昇\( \ \Delta T \ \mathrm {[℃]} \ \)するのに必要な熱量\( \ Q \ \mathrm {[kJ]} \ \)は，
\[
\begin{eqnarray}
Q &=&c\rho W\Delta T \\[ 5pt ] \end{eqnarray}
\] と求められます。

【解答】

(1)解答：ヨ
題意より，解答候補は（ロ）還元，（チ）中和，（ヨ）酸化，となると思います。
ワンポイント解説「1.燃料電池の概念図」の通り，アノードでは水素を酸化反応させ，電子を取り出します。

(2)解答：カ
題意より，解答候補は（ハ）エネルギー保存則，（ル）ファラデー効率，（カ）カルノー効率，となると思います。
カルノー効率とは熱源の温度差により決まる効率のことで，熱機関で使用される効率です。
エネルギー保存則はどのような反応でも成立し，ファラデー効率は全電力に対する生成物に寄与した電力のことをいうので不適切となります。

(3)解答：ニ
題意より，解答候補は（イ）テフロン膜，（ニ）イオン交換膜，（ワ）ポリスルフォン膜，となると思います。
ワンポイント解説「2.代表的な燃料電池」の通り，固体高分子形の燃料電池の電解質に用いるのはイオン交換膜となります。

(4)解答：リ
燃料\( \ 1 \ \mathrm {Nm^{3}} \)から発熱する熱量\( \ Q \ \mathrm {[kJ]} \)は，燃料の発熱量が\( \ 45 \ \mathrm {MJ/Nm^{3}} \)であるから，
\[
\begin{eqnarray}
Q&=&45\times 10^{3}\times 1 \\[ 5pt ] &=&45000 \ \mathrm {[kJ]} \\[ 5pt ] \end{eqnarray}
\] となるので，得られる電力量\( \ W \ \mathrm {[kW\cdot h]} \)は，ワンポイント解説「3.熱量と電力量の関係」及び発電効率が\( \ 40 \ \mathrm {[％]} \ \)であることから，
\[
\begin{eqnarray}
W&=&\frac {Q}{3600}\times 0.4 \\[ 5pt ] &=&\frac {45000}{3600}\times 0.4 \\[ 5pt ] &=&5 \ \mathrm {[kW\cdot h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
燃料の持つ化学エネルギーに対する総合効率が\( \ \eta =0.97 \ \)，発電効率が\( \ \eta _{\mathrm {g}} =0.40 \ \)であることから，全エネルギー\( \ Q=45000 \ \mathrm {[kJ]} \)のうち加熱に使用されるエネルギー\( \ Q_{\mathrm {h}} \ \mathrm {[kJ]} \)は，
\[
\begin{eqnarray}
Q_{\mathrm {h}}&=&Q\left( \eta -\eta _{\mathrm {g}} \right) \\[ 5pt ] &=&45000\times \left( 0.97 -0.40 \right)\\[ 5pt ] &=&25650 \ \mathrm {[kJ]} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「4.水の温度上昇\( \ \Delta T \ \)と熱量\( \ Q \ \)の関係」の通り，温度上昇\( \ \Delta T=40 \ \mathrm {[℃]} \ \)，水の比熱\( \ c=4.18 \ \mathrm {[kJ／\left( kg\cdot K\right) ]} \ \)，水の比重\( \ \rho =1000 \ \mathrm {[kg／m^{3}]} \ \)であるから，温められる水の量\( \ V \ \mathrm {[L]} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {h}} &=&c\rho \cdot \frac {V}{1000}\cdot \Delta T \\[ 5pt ] V &=&\frac {1000Q_{\mathrm {h}}}{c\rho \Delta T} \\[ 5pt ] &=&\frac {1000\times 25650}{4.18 \times 1000 \times 40} \\[ 5pt ] &≒&153 \ \mathrm {[L]} \\[ 5pt ] \end{eqnarray}
\] と求められる。