《機械》〈照明〉[R03:問5]天井面に設置した円板光源の配光特性に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，円板光源に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

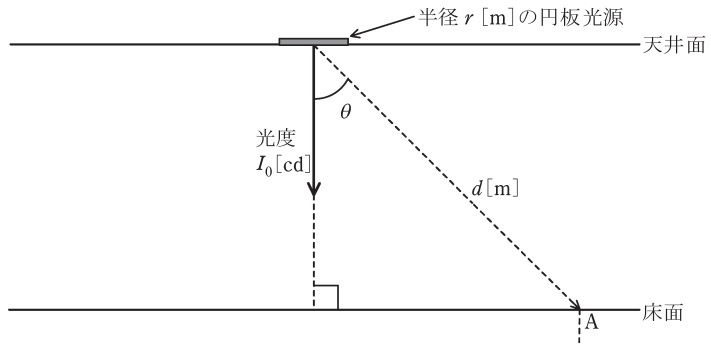
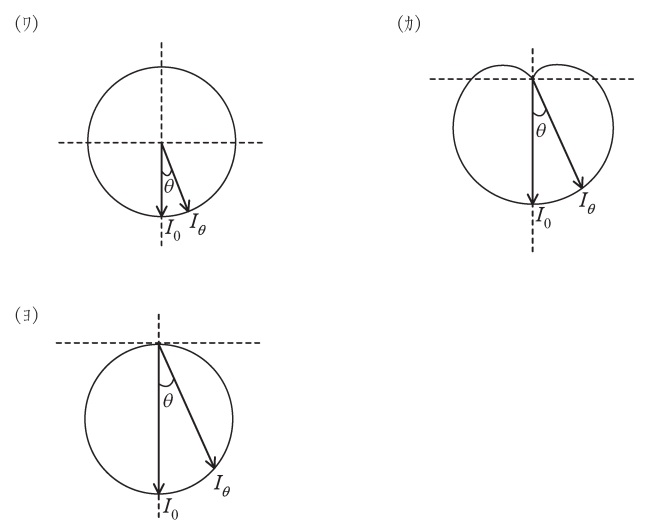
均等拡散面とみなせる円板光源がある。円板光源の発光面は平面で，片面のみが発光する。また，円板光源の厚さは無視できる。この円板光源の発光面の中心における法線方向の光度を$ \ I_{\mathrm {0}} \ \mathrm {[cd]} \ $とする。法線となす角$ \ \theta \ $の方向の光度$ \ I_{\mathrm {\theta }} \ \mathrm {[cd]} \ $は$ \ \fbox {　（１）　} \ $で与えられ，その配光曲線は$ \ \fbox {　（２）　} \ $のようになる。また，円板光源の全光束$ \ F \ \mathrm {[lm]} \ $は$ \ \fbox {　（３）　} \ $で与えられる。ただし，円周率は$ \ \pi \ $とする。

次に，図に示すように，半径$ \ r \ \mathrm {[m]} \ $のこの円板光源を部屋の天井面に取り付け，部屋の照明を行った。図において，床面上の$ \ \mathrm {A} \ $点から円板光源の中心を見たときの輝度$ \ L_{\mathrm {\theta }} \ \mathrm {[cd / m^{2}]} \ $は$ \ \fbox {　（４）　} \ $となり，$ \ \mathrm {A} \ $点における水平面照度$ \ E_{\theta h} \ \mathrm {[lx]} \ $は$ \ \fbox {　（５）　} \ $で与えられる。ただし，$ \ \mathrm {A} \ $点から円板光源の中心までの距離は$ \ d \ \mathrm {[m]} \ $であり，$ \ d ≫ r \ $とする。また，この部屋にはこの円板光源以外に光源はなく，天井，床，壁など，周囲からの反射光や入射光の影響はないものとする。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　I_{\mathrm {0}}\cos \theta　　　　　&（ロ）&　\frac {I_{\mathrm {0}}\cos \theta }{d^{2}}　　　　　&（ハ）&　\frac {I_{\mathrm {0}}}{\pi r^{2}\cos \theta } \\[ 5pt ] &（ニ）&　2\pi I_{\mathrm {0}}　　　　　&（ホ）&　　\frac {I_{\mathrm {0}}\cos ^{2}\theta }{d^{2}}　　　　　&（ヘ）&　4\pi I_{\mathrm {0}} \\[ 5pt ] &（ト）&　\frac {I_{\mathrm {0}}\left( 1+\cos \theta \right) \cos \theta }{2d^{2}}　　　　　&（チ）&　\frac {I_{\mathrm {0}}\cos \theta }{\pi r^{2}}　　　　　　　&（リ）&　\frac {I_{\mathrm {0}}\left( 1+\cos \theta \right) }{2} \\[ 5pt ] &（ヌ）&　\pi I_{\mathrm {0}}　　　　　&（ル）&　\frac {I_{\mathrm {0}}}{\pi r^{2}}　　　　　&（ヲ）&　I_{\mathrm {0}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

円板光源の配光に関する問題です。
(3)の全光束を求める問題が立体角や配光の考え方を理解していないと解けない問題ですが，それ以外の問題は基本公式を理解していれば解ける問題です。
配点が大きいので，高得点を目指して取り組んでいきましょう。

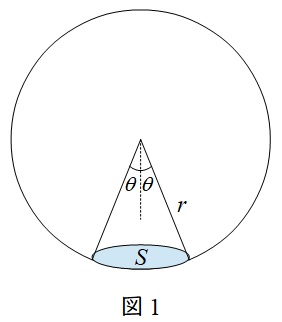
1.立体角の定義
図1のように球体があり，半径$ \ r \ \mathrm {[m]} \ $の錐体が球面を切り取った時の面積を$ \ S \ \mathrm {[m^{2}]} \ $とすると，立体角$ \ \omega \ \mathrm {[sr]} \ $は，
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，平面角$ \ \theta \ \mathrm {[rad]} \ $で表すと，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。球全体の立体角は$ \ \theta = \pi \ $の時であり，$ \ \omega =4\pi \ $となります。

2.光度$ \ I \ $
ある方向に向かう光束$ \ F \ $を立体角$ \ \omega \ $で割ったものが光度$ \ I \ $となります。
\[
\begin{eqnarray}
I &=&\frac {\Delta F}{\Delta \omega } \\[ 5pt ] \end{eqnarray}
\]

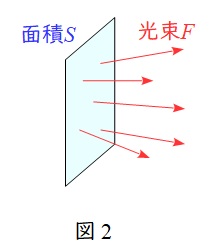
3.光束発散度$ \ M \ $
光源・反射面・透過面等の単位面積あたりから発散する光束をいい，面積$ \ S \ $から発散する光束を$ \ F \ $とすると，
\[
\begin{eqnarray}
M&=&\frac {F}{S} \ [ \mathrm {lm/m^{2}}] \\[ 5pt ] \end{eqnarray}
\] の関係があります。

4.輝度$ \ L \ $
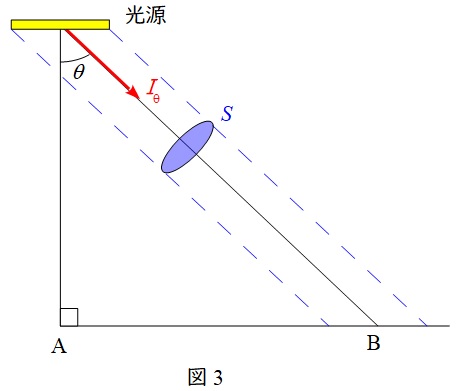
図3に示すように，$ \ \mathrm {B} \ $点から見た輝度は$ \ \mathrm {B} \ $点から見た光源のまぶしさを表す指標で，$ \ \mathrm {B} \ $点から照明を見た投影面積を$ \ S \ $とすると，
\[
\begin{eqnarray}
L&=&\frac {I_{\mathrm {\theta }}}{S} \ [ \mathrm {cd/m^{2}}] \\[ 5pt ] \end{eqnarray}
\] で求められます。

5.逆$ \ 2 \ $乗の法則
照度$ \ E \ $と光度$ \ I \ $と光源からの距離$ \ l \ $の間に，
\[
\begin{eqnarray}
E&=&\frac {I}{l^{2}} \\[ 5pt ] \end{eqnarray}
\] が成立するという法則です。

6.水平面照度
図3における$ \ E_{\mathrm {n}} \ $を法線照度，$ \ E_{\mathrm {h}} \ $を水平面照度と言い，以下のような関係があります。
\[
\begin{eqnarray}
E_{\mathrm {n}}&=&\frac {I_{\theta }}{l^{2}} \\[ 5pt ] E_{\mathrm {h}}&=&E_{\mathrm {\mathrm {n}}}\cos\theta \\[ 5pt ] &=&\frac {I_{\theta }\cos\theta }{l^{2}} \\[ 5pt ] \end{eqnarray}
\] ※　ランベルトの余弦法則は$ \ E_{\mathrm {h}}=E_{\mathrm {\mathrm {n}}}\cos \theta \ $のことを言います。

【解答】

(1)解答：イ
ワンポイント解説「6.水平面照度」図4の通り，法線となす角$ \ \theta \ $の方向の光度$ \ I_{\mathrm {\theta }} \ \mathrm {[cd]} \ $は，
\[
\begin{eqnarray}
I_{\mathrm {\theta }}&=&I_{\mathrm {0}}\cos\theta \\[ 5pt ] \end{eqnarray}
\] で与えられる。

(2)解答：ヨ
円板光源における配光曲線は（ヨ）のようになります。

(3)解答：ヌ
円板光源の全光束$ \ F \ \mathrm {[lm]} \ $は，ワンポイント解説「2.光度$ \ I \ $」の通り，
\[
\begin{eqnarray}
\mathrm {d} F &=&I_{\mathrm {\theta }}\mathrm {d} \omega \\[ 5pt ] \int \mathrm {d} F &=&\int I_{\mathrm {\theta }}\mathrm {d} \omega \\[ 5pt ] F &=&\int I_{\mathrm {0}}\cos \theta \mathrm {d} \omega \\[ 5pt ] \end{eqnarray}
\] となる。ここで，ワンポイント解説「1.立体角の定義」より，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \frac {\mathrm {d} \omega }{\mathrm {d} \theta } &=&2\pi \sin \theta \\[ 5pt ] \mathrm {d} \omega &=&2\pi \sin \theta \mathrm {d} \theta \\[ 5pt ] \end{eqnarray}
\] であり，$ \ \displaystyle 0≦\theta ≦\frac {\pi}{2} \ $であるため，
\[
\begin{eqnarray}
F &=&\int I_{\mathrm {0}}\cos \theta \mathrm {d} \omega \\[ 5pt ] &=&\int _{0}^{\frac {\pi }{2}}I_{\mathrm {0}}\cos \theta \cdot 2\pi \sin \theta \mathrm {d} \theta \\[ 5pt ] &=&\pi I_{\mathrm {0}}\int _{0}^{\frac {\pi }{2}}2\sin \theta \cos \theta\mathrm {d} \theta \\[ 5pt ] &=&\pi I_{\mathrm {0}}\int _{0}^{\frac {\pi }{2}}\sin {2\theta } \mathrm {d} \theta \\[ 5pt ] &=&\pi I_{\mathrm {0}}\left[ -\frac {1}{2}\cos 2\theta \right] _{0}^{\frac {\pi }{2}} \\[ 5pt ] &=&\pi I_{\mathrm {0}}\left( \frac {1}{2}+\frac {1}{2}\right) \\[ 5pt ] &=&\pi I_{\mathrm {0}}\\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
半径$ \ r \ \mathrm {[m]} \ $の円板光源を$ \ \mathrm {A} \ $点から見たときの見かけの面積$ \ S_{\mathrm {\theta }} \ \mathrm {[m^{2}]} \ $は，
\[
\begin{eqnarray}
S_{\mathrm {\theta }} &=&\pi r^{2}\cos \theta \\[ 5pt ] \end{eqnarray}
\] であるから，ワンポイント解説「4.輝度$ \ L \ $」の通り，$ \ \mathrm {A} \ $点から円板光源の中心を見たときの輝度$ \ L_{\mathrm {\theta }} \ \mathrm {[cd / m^{2}]} \ $は，
\[
\begin{eqnarray}
L_{\mathrm {\theta }} &=&\frac {I_{\mathrm {\theta }}}{S_{\mathrm {\theta }}} \\[ 5pt ] &=&\frac {I_{\mathrm {0}}\cos \theta }{\pi r^{2}\cos \theta } \\[ 5pt ] &=&\frac {I_{\mathrm {0}}}{\pi r^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
ワンポイント解説「6.水平面照度」の通り，$ \ \mathrm {A} \ $点における水平面照度$ \ E_{\theta h} \ \mathrm {[lx]} \ $は，
\[
\begin{eqnarray}
E_{\theta h}&=&\frac {I_{\mathrm {\theta }}\cos \theta }{d^{2}} \\[ 5pt ] &=&\frac {I_{\mathrm {0}}\cos ^{2}\theta }{d^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。