【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,三相誘導電動機の特性算定に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
線間電圧\( \ V \ \mathrm {[V]} \ \)の交流電源に三相誘導電動機を接続した場合,星形\( \ 1 \ \)相一次換算の\( \ \mathrm {L} \ \)形等価回路における一次側及び二次側の巻線抵抗をそれぞれ\( \ r_{1} \ \mathrm {[\Omega ]} \ \)及び\( \ {r_{2}}^{\prime } \ \mathrm {[\Omega ]} \ \),一次側及び二次側の漏れリアクタンスをそれぞれ\( \ x_{1} \ \mathrm {[\Omega ]} \ \)及び\( \ {x_{2}}^{\prime } \ \mathrm {[\Omega ]} \ \),励磁回路のコンダクタンスを\( \ g_{0} \ \mathrm {[S]} \ \),サセプタンスを\( \ b_{0} \ \mathrm {[S]} \ \),滑りを\( \ s \ \)とすれば,一次負荷電流\( \ {\dot I_{1}}^{\prime } \ \mathrm {[A]} \ \)は次式で表される。
\[
\begin{eqnarray}
{\dot I_{1}}^{\prime } &=& \frac {\displaystyle \frac {V}{\sqrt {3}}}{\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}+\mathrm {j}\left( x_{1}+{x_{2}}^{\prime }\right) } \\[ 5pt ]
\end{eqnarray}
\]
また,励磁電流\( \ \dot I_{0} \ \mathrm {[A]} \ \)は電源電圧を基準とすると,\( \ \displaystyle \dot I_{0}=\frac {V}{\sqrt {3}}\left( \ \fbox { (1) } \ \right) \ \)で表される。よって,一次電流の大きさ\( \ I_{1} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{1} &=& \frac {V}{\sqrt {3}}\sqrt {\left( g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{Z^{2}}\right) ^{2}+\left( b_{0}+ \ \fbox { (2) } \ \right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ただし,\( \ Z=\sqrt {\left( \displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s} \right) ^{2}+\left( x_{1}+{x_{2}}^{\prime }\right) ^{2}} \ \mathrm {[\Omega ]} \ \)とする。
力率\( \ \cos \theta \ \),及び一次入力\( \ P_{1} \ \mathrm {[W]} \ \)は,それぞれ,
\[
\begin{eqnarray}
\cos \theta &=& \frac { \ \fbox { (3) } \ }{\sqrt {\left( g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{\displaystyle Z^{2}}\right) ^{2}+\left( b_{0}+ \ \fbox { (2) } \ \right) ^{2}}} \\[ 5pt ]
P_{1} &=& \left( g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{Z^{2}}\right) \times \ \fbox { (4) } \ \\[ 5pt ]
\end{eqnarray}
\]
となる。二次入力を\( \ P_{2} \ \mathrm {[W]} \ \),機械的出力を\( \ P_{0} \ \mathrm {[W]} \ \),機械損を無視すれば,効率\( \ \eta \ \)は次式で表せる。
\[
\begin{eqnarray}
\eta &=&\frac {P_{0}}{P_{1}}\times 100 = \ \fbox { (5) } \ \times \frac {P_{2}}{P_{1}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {V^{2}}{3} &(ロ)& g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{2Z^{2}} &(ハ)& V^{2} \\[ 5pt ]
&(ニ)& 3V^{2} &(ホ)& g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{Z^{2}} &(ヘ)& g_{0}-\mathrm {j}b_{0} \\[ 5pt ]
&(ト)& \frac {\displaystyle x_{1}+{x_{2}}^{\prime }}{Z^{2}} &(チ)& \frac {1-s}{s} &(リ)& \frac {\displaystyle x_{1}+{x_{2}}^{\prime }}{2Z^{2}} \\[ 5pt ]
&(ヌ)& b_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{Z^{2}} &(ル)& \frac {1}{g_{0}}-\mathrm {j}\frac {1}{b_{0}} &(ヲ)& \frac {s}{1-s} \\[ 5pt ]
&(ワ)& g_{0}+\mathrm {j}b_{0} &(カ)& \frac {\displaystyle x_{1}+2{x_{2}}^{\prime }}{Z^{2}} &(ヨ)& \left( 1-s \right) \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三相誘導電動機の特性計算に関する問題です。
少しだけ計算量は多いですが,\( \ 2 \ \)種でもよく出題されてきた\( \ \mathrm {L} \ \)形等価回路の内容なので,多くの受験生が高得点を取得してくると予想されます。
\( \ 1 \ \)種では二次試験でも高い計算能力が求められますので,本問も1問あたりの目安である\( \ 15 \ \)分以内で解けることを目標として下さい。
1.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
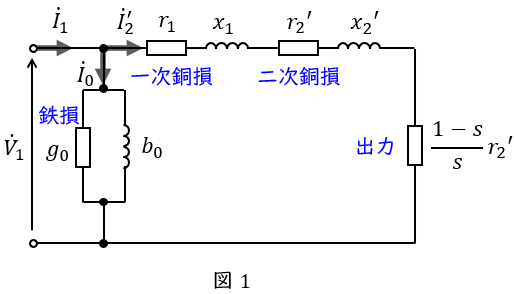
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧(相電圧),\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \),二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \),出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。
【解答】
(1)解答:ヘ
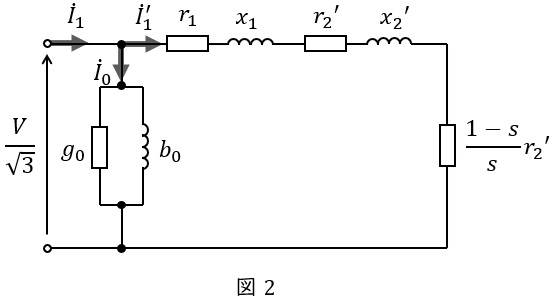
題意に沿って\( \ \mathrm {L} \ \)形等価回路を描くと図2のようになる。
図2の励磁回路にキルヒホッフの法則を適用すると,
\[
\begin{eqnarray}
\dot I_{0}&=&\frac {V}{\sqrt {3}}\left( g_{0}-\mathrm {j}b_{0} \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ト
一次電流\( \ \dot I_{1} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
\dot I_{1}&=&\dot I_{0}+{\dot I_{1}}^{\prime } \\[ 5pt ]
&=&\frac {V}{\sqrt {3}}\left( g_{0}-\mathrm {j}b_{0} \right) +\frac {\displaystyle \frac {V}{\sqrt {3}}}{\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}+\mathrm {j}\left( x_{1}+{x_{2}}^{\prime }\right) } \\[ 5pt ]
&=&\frac {V}{\sqrt {3}}\left( g_{0}-\mathrm {j}b_{0} \right) +\frac {V}{\sqrt {3}}\frac {1}{\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}+\mathrm {j}\left( x_{1}+{x_{2}}^{\prime }\right) }\times \frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}-\mathrm {j}\left( x_{1}+{x_{2}}^{\prime }\right) }{\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}-\mathrm {j}\left( x_{1}+{x_{2}}^{\prime }\right) } \\[ 5pt ]
&=&\frac {V}{\sqrt {3}}\left( g_{0}-\mathrm {j}b_{0} \right) +\frac {V}{\sqrt {3}}\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}-\mathrm {j}\left( x_{1}+{x_{2}}^{\prime }\right) }{\displaystyle \left( \displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s} \right) ^{2}+\left( x_{1}+{x_{2}}^{\prime }\right) ^{2} } \\[ 5pt ]
&=&\frac {V}{\sqrt {3}}\left( g_{0}-\mathrm {j}b_{0} \right) +\frac {V}{\sqrt {3}}\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}-\mathrm {j}\left( x_{1}+{x_{2}}^{\prime }\right) }{\displaystyle Z^{2} } \\[ 5pt ]
&=&\frac {V}{\sqrt {3}}\left\{ g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{\displaystyle Z^{2} }-\mathrm {j}\left( b_{0}+\frac {\displaystyle x_{1}+{x_{2}}^{\prime } }{\displaystyle Z^{2} }\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その大きさ\( \ I_{1} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{1}&=&\frac {V}{\sqrt {3}}\sqrt {\left( g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{Z^{2}}\right) ^{2}+\left( b_{0}+\frac {\displaystyle x_{1}+{x_{2}}^{\prime } }{\displaystyle Z^{2} } \right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ホ
(2)解答式より,力率\( \ \cos \theta \ \)は,
\[
\begin{eqnarray}
\cos \theta &=& \frac { \displaystyle g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{Z^{2}} }{\sqrt {\left( g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{\displaystyle Z^{2}}\right) ^{2}+\left( b_{0}+ \frac {\displaystyle x_{1}+{x_{2}}^{\prime } }{\displaystyle Z^{2} } \right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ハ
(2)より,一次入力\( \ P_{1} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{1} &=& \sqrt {3}V\cdot \mathrm {Re}\left[ \dot I_{1}\right] \\[ 5pt ]
&=& \sqrt {3}V \cdot \frac {V}{\sqrt {3}}\left( g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{\displaystyle Z^{2} } \right) \\[ 5pt ]
&=& \left( g_{0}+\frac {\displaystyle r_{1}+\frac {{r_{2}}^{\prime }}{s}}{\displaystyle Z^{2} } \right) \times V^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヨ
ワンポイント解説「1.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係」の通り,\( \ P_{0}=P_{2}\left( 1-s \right) \ \)なので,
\[
\begin{eqnarray}
\eta &=&\frac {P_{0}}{P_{1}}\times 100 \\[ 5pt ]
&=&\frac {P_{2}\left( 1-s \right) }{P_{1}}\times 100 \\[ 5pt ]
&=&\left( 1-s \right) \times \frac {P_{2}}{P_{1}}\times 100 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん