【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,単相誘導電動機に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)の(1)から(3)については,最も適切な語句又は式を解答群の中から選び,その記号を答案用紙に,また,(4)から(7)については値を求め答案用紙に記入しなさい。
単相誘導電動機の単相巻線に交流電流を流すと交番磁界が発生する。この交番磁界は互いに反対方向に同期速度で回転し,大きさが交番磁界の\( \ \displaystyle \frac {1}{2} \ \)である二つの回転磁界に分解できる。回転子が静止しているとき,これらの回転磁界は互いに逆方向のトルクを生じさせるので,始動トルクは零となる。しかし,どちらかの方向に少し回してやると回転子はその方向に加速し,同期速度に近い速度で定常運転に入る。
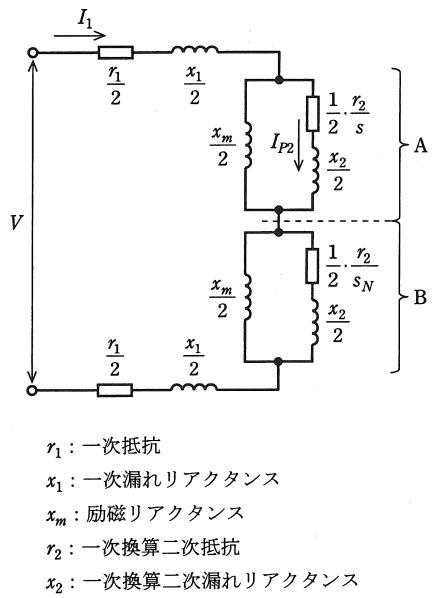
単相誘導電動機は,互いに反対方向に回転する二つの回転磁界が存在することから,回転子が機械的に直結され,回転磁界の回転方向が異なる二つの同じ二相誘導電動機と考え,その等価回路は図のように表すことができる。等価回路の\( \ \mathrm {A} \ \)の部分は回転子の回転方向と同方向にトルクを発生する\( \ \fbox { (1) } \ \)電動機,\( \ \mathrm {B} \ \)の部分は回転方向と逆方向のトルクを発生する\( \ \fbox { (2) } \ \)電動機の等価回路である。\( \ \fbox { (1) } \ \)電動機の滑りを\( \ s \ \)とするとき,\( \ \fbox { (2) } \ \)電動機の滑り\( \ s_{N} \ \)は\( \ \fbox { (3) } \ \)となる。
定格\( \ 200 \ \mathrm {[W]} \ \),\( \ 100 \ \mathrm {[V]} \ \)の単相誘導電動機が定格電圧のもと,滑り\( \ s=0.03 \ \)で運転している。定格を基準とする単位法で表した回路定数は\( \ r_{1} = 0.04 \ \mathrm {[p.u.]} \ \),\( \ x_{1} = 0.04 \ \mathrm {[p.u.]} \ \),\( \ r_{2} = 0.042 \ \mathrm {[p.u.]} \ \),\( \ x_{2} = 0.06 \ \mathrm {[p.u.]} \ \),\( \ x_{m} = 2 \ \mathrm {[p.u.]} \ \)である。ただし,等価回路\( \ \mathrm {B} \ \)の部分の計算において,滑り\( \ s \ \)が小さい範囲では\( \ \displaystyle \frac {1}{2}\cdot \frac {r_{2}}{s_{N}}≒\frac {1}{2}\cdot \frac {r_{2}}{2} \ \)とし,また,\( \ \displaystyle \frac {x_{m}}{2} \ \)は\( \ \displaystyle \left| \frac {1}{2}\cdot \frac {r_{2}}{2}+\mathrm {j}\frac {x_{2}}{2}\right| \ \)と比べて大きいので\( \ \displaystyle \frac {x_{m}}{2} \ \)に流れる電流を無視して計算せよ。
(4) 入力インピーダンス\( \ Z \ \mathrm {[p.u.]} \ \)
(5) 一次電流の大きさ\( \ I_{1} \ \mathrm {[A]} \ \)
(6) 等価回路\( \ \mathrm {A} \ \)の二次電流の大きさ\( \ I_{P2} \ \mathrm {[A]} \ \)(一次換算値)
(7) 同期ワットで表したトルク\( \ T \ \mathrm {[W]} \ \)
〔(1)~(3)の解答群〕
\[
\begin{eqnarray}
&(イ)& 零相分 &(ロ)& 逆相分 &(ハ)& 分 相 \\[ 5pt ]
&(ニ)& 同相分 &(ホ)& 反作用 &(ヘ)& 正相分 \\[ 5pt ]
&(ト)& 3-s &(チ)& 2-s &(リ)& 1-s \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
単相誘導電動機に関する知識を問い,等価回路を用いた計算を行う問題です。
考え方自体はそれほど難解ではありませんが,(4)の計算が多く,機械制御の制限時間を考えるとかなり厳しい問題であったかなと思います。
1.オーム法から単位法への変換
基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)の時,インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)を単位法で表すと,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ [\Omega ] \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}} (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
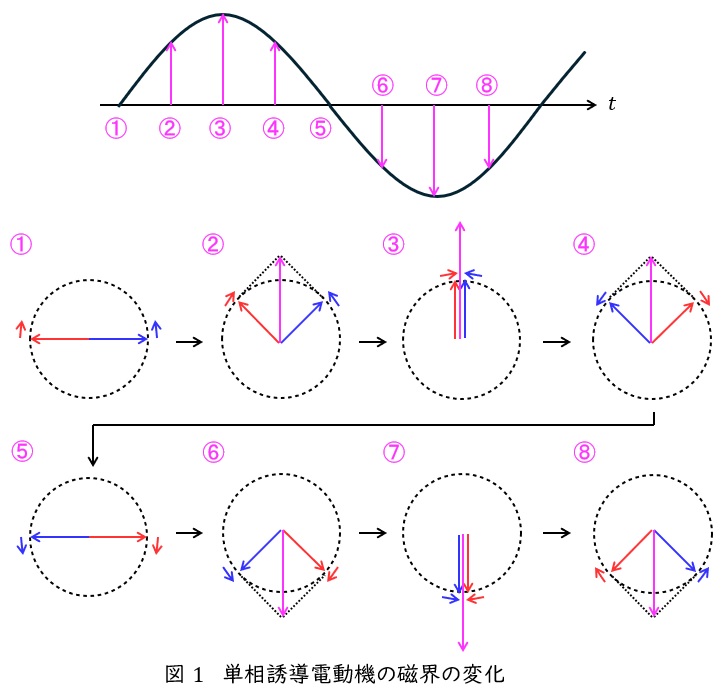
2.単相誘導電動機の磁界の変化
単相誘導電動機は単相の交番磁界により運転する電動機であり,単相の交番磁界は図1のように正方向の回転磁界(青矢印)と逆方向の回転磁界(赤矢印)に分けることができ,\( \ 2 \ \)つの回転磁界を合わせたものと考えることができます。
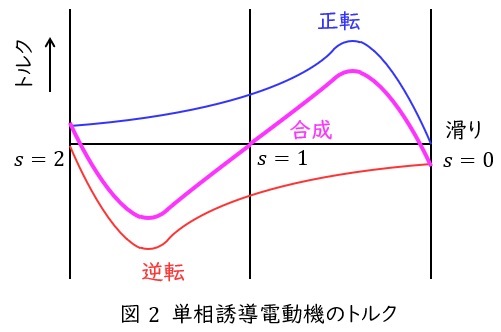
回転磁界によるトルク特性は図2の青線と赤線で表されるので,その合成トルクは紫線のようになり,始動時に回転磁界が発生せず,仮にどちらかに動いた場合にはそちら側にトルクがかかるようになることが分かります。
回転子が回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)で正回転しているとき,正相分回転磁界の回転速度を\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)とすれば,正相分に対する滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s&=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,逆相分回転磁界の回転速度を\( \ -N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)とすれば,逆相分に対する滑り\( \ s^{\prime } \ \)は,
\[
\begin{eqnarray}
s^{\prime }&=&\frac {-N_{\mathrm {s}}-N}{-N_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {-2N_{\mathrm {s}}+\left( N_{\mathrm {s}}-N\right) }{-N_{\mathrm {s}}} \\[ 5pt ]
&=&\frac {2N_{\mathrm {s}}-\left( N_{\mathrm {s}}-N\right) }{N_{\mathrm {s}}} \\[ 5pt ]
&=&2-s \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ヘ
ワンポイント解説「2.単相誘導電動機の磁界の変化」の通り,回転子の回転方向と同方向にトルクを発生するのは正相分電動機といいます。
(2)解答:ロ
ワンポイント解説「2.単相誘導電動機の磁界の変化」の通り,回転子の回転方向と逆方向のトルクを発生するのは逆相分電動機といいます。
(3)解答:チ
ワンポイント解説「2.単相誘導電動機の磁界の変化」の通り,正相分電動機の滑りを\( \ s \ \)としたときの逆相分電動機の滑り\( \ s_{N} \ \)は\( \ 2-s \ \)となります。
(4)入力インピーダンス\( \ Z \ \mathrm {[p.u.]} \ \)
等価回路の\( \ \mathrm {A} \ \)の部分のインピーダンス\( \ {\dot Z}_{A} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{A}&=&\frac {\displaystyle \mathrm {j}\frac {x_{m}}{2}\cdot \left( \frac {1}{2}\cdot \frac {r_{2}}{s}+\mathrm {j}\frac {x_{2}}{2}\right) }{\displaystyle \mathrm {j}\frac {x_{m}}{2}+\left( \frac {1}{2}\cdot \frac {r_{2}}{s}+\mathrm {j}\frac {x_{2}}{2}\right) } \\[ 5pt ]
&=&\frac {\displaystyle \mathrm {j}\frac {2}{2}\times \left( \frac {1}{2}\times \frac {0.042}{0.03}+\mathrm {j}\frac {0.06}{2}\right) }{\displaystyle \mathrm {j}\frac {2}{2}+ \left( \frac {1}{2}\times \frac {0.042}{0.03}+\mathrm {j}\frac {0.06}{2}\right) } \\[ 5pt ]
&=&\frac {-0.03+\mathrm {j}0.7}{0.7+\mathrm {j}1.03} \\[ 5pt ]
&=&\frac {-0.03+\mathrm {j}0.7}{0.7+\mathrm {j}1.03}\times \frac {0.7-\mathrm {j}1.03}{0.7-\mathrm {j}1.03} \\[ 5pt ]
&=&\frac {0.7+\mathrm {j}0.520 \ 9}{1.550 \ 9} \\[ 5pt ]
&≒&0.451 \ 35+\mathrm {j}0.335 \ 87 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,等価回路の\( \ \mathrm {B} \ \)の部分のインピーダンス\( \ {\dot Z}_{B} \ \mathrm {[p.u.]} \ \)は,\( \ \displaystyle \frac {1}{2}\cdot \frac {r_{2}}{s_{N}}≒\frac {1}{2}\cdot \frac {r_{2}}{2} \ \)とし,\( \ \displaystyle \frac {x_{m}}{2} \ \)に流れる電流を無視するので,
\[
\begin{eqnarray}
{\dot Z}_{B}&≒&\frac {1}{2}\cdot \frac {r_{2}}{s_{N}}+\mathrm {j}\frac {x_{2}}{2} \\[ 5pt ]
&≒&\frac {1}{2}\cdot \frac {r_{2}}{2}+\mathrm {j}\frac {x_{2}}{2} \\[ 5pt ]
&=&\frac {1}{2}\times \frac {0.042}{2}+\mathrm {j}\frac {0.06}{2} \\[ 5pt ]
&=&0.010 \ 5+\mathrm {j}0.03 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,入力インピーダンス\( \ \dot Z \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
\dot Z&=&\frac {r_{1}}{2}+\mathrm {j} \frac {x_{1}}{2}+{\dot Z}_{A}+{\dot Z}_{B}+\frac {r_{1}}{2}+\mathrm {j} \frac {x_{1}}{2} \\[ 5pt ]
&=&r_{1}+\mathrm {j} x_{1}+{\dot Z}_{A}+{\dot Z}_{B} \\[ 5pt ]
&=&0.04+\mathrm {j} 0.04+0.451 \ 35+\mathrm {j}0.335 \ 87+0.010 \ 5+\mathrm {j}0.03 \\[ 5pt ]
&=&0.501 \ 85+\mathrm {j}0.405 \ 87 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その大きさ\( \ Z \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
Z&=&\sqrt {0.501 \ 85^{2}+0.405 \ 87^{2}} \\[ 5pt ]
&≒&0.645 \ 43 → 0.645 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)一次電流の大きさ\( \ I_{1} \ \mathrm {[A]} \ \)
題意より,定格電圧で運転しているので,\( \ V_{1}=1.0 \ \mathrm {[p.u.]} \ \)であるから,一次電流\( \ I_{1} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
I_{1}&=&\frac {V_{1}}{Z} \\[ 5pt ]
&=&\frac {1.0}{0.645 \ 43} \\[ 5pt ]
&≒&1.549 \ 4 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,定格電流\( \ I_{n} \ \mathrm {[A]} \ \)は,定格容量\( \ P_{n}=200 \ \mathrm {[W]} \ \)及び定格電圧\( \ V_{n}=100 \ \mathrm {[V]} \ \)より,
\[
\begin{eqnarray}
I_{n}&=&\frac {P_{n}}{V_{n}} \\[ 5pt ]
&=&\frac {200}{100} \\[ 5pt ]
&=&2.0 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,一次電流の大きさ\( \ I_{1} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{1}&=&I_{1} \ \mathrm {[p.u.]}\times I_{n} \\[ 5pt ]
&=&1.549 \ 4\times 2 \\[ 5pt ]
&=&3.098 \ 8 → 3.10 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)等価回路\( \ \mathrm {A} \ \)の二次電流の大きさ\( \ I_{P2} \ \mathrm {[A]} \ \)(一次換算値)
等価回路\( \ \mathrm {A} \ \)の二次電流の大きさ\( \ I_{P2} \ \mathrm {[A]} \ \)は,分流の法則より,
\[
\begin{eqnarray}
I_{P2}&=&\left| \frac {\displaystyle \mathrm {j}\frac {x_{m}}{2}}{\displaystyle \mathrm {j}\frac {x_{m}}{2}+\left( \frac {1}{2}\cdot \frac {r_{2}}{s}+\mathrm {j}\frac {x_{2}}{2}\right) }\right| I_{1} \\[ 5pt ]
&=&\left| \frac {\displaystyle \mathrm {j}\frac {2}{2}}{\displaystyle \mathrm {j}\frac {2}{2}+ \left( \frac {1}{2}\cdot \frac {0.042}{0.03}+\mathrm {j}\frac {0.06}{2}\right) }\right| I_{1} \\[ 5pt ]
&=&\left| \frac {\mathrm {j}}{0.7+\mathrm {j}1.03}\right| \times 3.098 \ 8 \\[ 5pt ]
&=&\frac {1}{\sqrt {0.7^{2}+1.03^{2}}} \times 3.098 \ 8 \\[ 5pt ]
&≒&2.488 \ 3 → 2.49 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(7)同期ワットで表したトルク\( \ T \ \mathrm {[W]} \ \)
正相分の抵抗成分\( \ R_{A} \ \mathrm {[\Omega ]} \ \)及び逆相分の抵抗成分\( \ R_{B} \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「1.オーム法から単位法への変換」の通り
\[
\begin{eqnarray}
R_{A} \ \mathrm {[p.u.]} \ &=&\frac {P_{n}R_{A} \ [\Omega ] \ }{V_{n}^{2}} \\[ 5pt ]
R_{A} \ [\Omega ] \ &=&\frac {V_{n}^{2}}{P_{n}}R_{A} \ \mathrm {[p.u.]} \ \\[ 5pt ]
&=&\frac {V_{n}^{2}}{P_{n}}\cdot \frac {1}{2}\cdot \frac {r_{2}}{s} \\[ 5pt ]
&=&\frac {100^{2}}{200}\times \frac {1}{2}\times \frac {0.042}{0.03} \\[ 5pt ]
&=&35 \ \mathrm {[\Omega ]} \\[ 5pt ]
R_{B} \ [\Omega ] \ &=&\frac {V_{n}^{2}}{P_{n}}R_{B} \ \mathrm {[p.u.]} \ \\[ 5pt ]
&=&\frac {V_{n}^{2}}{P_{n}}\cdot \frac {1}{2}\cdot \frac {r_{2}}{2} \\[ 5pt ]
&=&\frac {100^{2}}{200}\times \frac {1}{2}\times \frac {0.042}{2} \\[ 5pt ]
&=&0.525 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,正相分のトルク\( \ T_{A} \ \mathrm {[W]} \ \)及び逆相分のトルク\( \ T_{B} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
T_{A}&=&R_{A}I_{P2}^{2} \\[ 5pt ]
&=&35\times 2.488 \ 3^{2} \\[ 5pt ]
&≒&216.71 \mathrm {[W]} \\[ 5pt ]
T_{B}&=&R_{B}I_{1}^{2} \\[ 5pt ]
&=&0.525\times 3.098 \ 8^{2} \\[ 5pt ]
&≒&5.0413 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
となる。単相誘導電動機の同期ワットで表したトルク\( \ T \ \mathrm {[W]} \ \)は,正相分のトルク\( \ T_{A} \ \mathrm {[W]} \ \)から逆相分のトルク\( \ T_{B} \ \mathrm {[W]} \ \)を差し引いたものであるから,
\[
\begin{eqnarray}
T&=&T_{A}-T_{B} \\[ 5pt ]
&=&216.71-5.0413 \\[ 5pt ]
&≒&212 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん