【問題】
【難易度】★★★★☆(やや難しい)
図は,三相巻線形誘導電動機の1相分の二次等価回路である。\(f_{0}\)は同期周波数,\(\omega _{0} ( =2\pi f_{0} )\)は同期角周波数,\(s {\dot E}_{2}\)は滑り\(s\)のときの二次誘導起電力,\({\dot I}_{2}\)(大きさ\(\left| {\dot I}_{2}\right| =I_{2}\) )は二次電流,\(r_{2}\)は二次巻線抵抗,\(x_{2}\)は\(\omega _{0}\)での二次回路リアクタンスであるとして,次の問に答えよ。ただし,励磁アドミタンス,一次巻線抵抗,一次漏れリアクタンス及び機械損は無視し,\(\omega _{0}\),\(\left| {\dot E}_{2}\right| =E_{2}\)は一定とする。
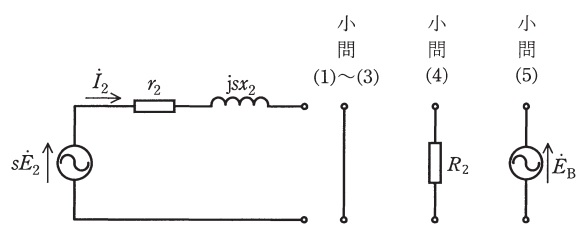
(1) 二次側端子を短絡して滑り\(s\)で運転しているときの,二次電流の大きさ\(\left| {\dot I}_{2}\right| =I_{2}\),及び二次入力(同期ワットで表したトルク)\(P_{2}\)を示せ。
(2) この電動機は,二次側端子を短絡して運転するとき滑り\(s_{\mathrm {m}}=0.2\)で最大トルクとなる。\(x_{2}=5r_{2}\)となることを示し,同期ワットで表した最大トルク\(P_{\mathrm {2m}}\)を\(E_{2}\)及び\(r_{2}\)で表せ。
(3) この電動機が,二次側端子を短絡して一定トルクをもつ負荷を駆動しているとき,滑りが\(s_{1}=0.02\)であった。二次入力\(P_{2}\),二次銅損\(P_{\mathrm {C2}}\)を,\(E_{2}\)及び\(r_{2}\)で表せ。\(x_{2}=5r_{2}\)の関係を用いよ。
(4) 二次側端子に抵抗\(R_{2}=r_{2}\)を挿入して,同じ一定トルクをもつ負荷を駆動したところ滑りが\(s_{2}\)となった。\(s_{2}\)を求めよ。このときの二次側損失\(P_{\mathrm {w2}}\)(二次銅損と抵抗\(R_{2}\)での損失の和)を,\(E_{2}\)及び\(r_{2}\)で表せ。\(x_{2}=5r_{2}\)の関係を用いよ。
(5) 抵抗\(R_{2}\)に代えて,双方向の電力変換ができる二次励磁回路を電源とみなし,図中矢印の方向に,\(s_{2}{\dot E}_{2}\)と同相で滑り周波数\(\left( s_{2}f_{0}\right) \)の二次励磁電圧\({\dot E}_{\mathrm {B}}\)(大きさ\(\left| {\dot E}_{\mathrm {B}}\right| =E_{\mathrm {B}}\) )を印加した。すなわち二次巻線に掛かる電圧は\(s_{2}{\dot E}_{2}-{\dot E}_{\mathrm {B}}\)であり,その大きさは\(\left| s_{2}{\dot E}_{2}-{\dot E}_{\mathrm {B}}\right| =s_{2}E_{2}-E_{\mathrm {B}}\)である。こうして,同じ一定トルクをもつ負荷を駆動したところ,滑りは変わらず\(s_{2}\)であった。\(E_{\mathrm {B}}\)を\(E_{2}\)で表せ。このときの二次銅損\(P^{\prime \prime }_{\mathrm {C2}}\)及び二次励磁回路へ返還する電力\(P_{\mathrm {B}}\)を,\(E_{2}\)及び\(r_{2}\)で表せ。\(x_{2}=5r_{2}\)の関係を用いよ。
【ワンポイント解説】
三相誘導電動機の問題は比較的過去問と似た問題も多く,理解してしまえば取り組みやすいですが,式が長くなり解くのに時間がかかるという欠点があります。電流や電力の導出はスピーディにできるようにしましょう。
1.三相誘導電動機の二次入力,出力,銅損
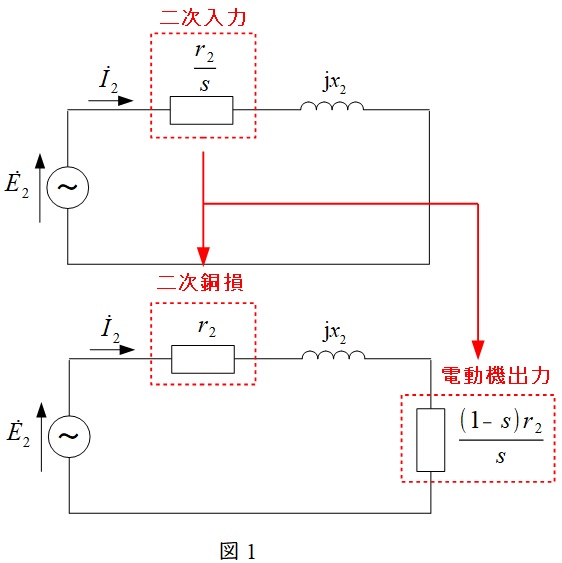
三相誘導電動機は図1に示すような簡易等価回路となります。(一般的に各値を\(\displaystyle \frac {1}{s}\)倍します。)この時,二次入力,出力,銅損の値は
\[
\begin{eqnarray}
入力&:&P_{2}&=&3\frac {r_{2}}{s}I_{2}^{2} \\[ 5pt ]
出力&:&P_{\mathrm {O}}&=&3\frac {\left( 1-s \right) r_{2}}{s}I_{2}^{2} \\[ 5pt ]
銅損&:&P_{\mathrm {C2}}&=&3r_{2}I_{2}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
入力:出力:銅損=1:(1-s):s
\]
の関係があります。
2.分数の微分
\(x\)についての関数\(u(x)\)と\(v(x)\)があるとき,\(\displaystyle \frac {u(x)}{v(x)}\)の微分は,
\[
\left[ \frac {u(x)}{v(x)}\right] ^{\prime } =\frac {u^{\prime }v-uv^{\prime }}{v^{2}}
\]
となります。
【解答】
(1)二次側端子を短絡して滑り\(s\)で運転しているときの,二次電流の大きさ\(\left| {\dot I}_{2}\right| =I_{2}\),及び二次入力(同期ワットで表したトルク)\(P_{2}\)
回路を流れる二次電流\({\dot I}_{2}\)は,
\[
{\dot I}_{2}=\frac {sE_{2}}{r_{2}+\mathrm {j}sx_{2}}
\]
であるから,その大きさ\(I_{2}\)は,
\[
I_{2}=\frac {sE_{2}}{\sqrt {r_{2}^{2}+\left( sx_{2}\right) ^{2}}}
\]
と求められる。また,二次入力\(P_{2}\)はワンポイント解説「1.三相誘導電動機の二次入力,出力,銅損」の通り,
\[
\begin{eqnarray}
P_{2}&=& 3\frac {r_{2}}{s}I_{2}^{2} \\[ 5pt ]
&=&3\frac {r_{2}}{s}\left( \frac {sE_{2}}{\sqrt {r_{2}^{2}+\left( sx_{2}\right) ^{2}}}\right) ^{2} \\[ 5pt ]
&=&\frac {3sr_{2}E_{2}^{2}}{r_{2}^{2}+\left( sx_{2}\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)滑り\(s_{\mathrm {m}}=0.2\)で最大トルクとなる時,\(x_{2}=5r_{2}\)となることを示し,同期ワットで表した最大トルク\(P_{\mathrm {2m}}\)を\(E_{2}\)及び\(r_{2}\)で表す
(1)で求めた二次入力の両辺を\(s\)について微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}P_{2}}{\mathrm {d}s}&=& \frac {3r_{2}E_{2}^{2}\left\{ r_{2}^{2}+\left( sx_{2}\right) ^{2}\right\} – 3sr_{2}E_{2}^{2}\cdot x_{2}\cdot 2sx_{2} }{\left\{ r_{2}^{2}+\left( sx_{2}\right) ^{2}\right\} ^{2}} \\[ 5pt ]
&=&\frac {3r_{2}E_{2}^{2}\left\{ r_{2}^{2}+\left( sx_{2}\right) ^{2}\right\} – 6s^{2}r_{2}x_{2}^{2}E_{2}^{2} }{\left\{ r_{2}^{2}+\left( sx_{2}\right) ^{2}\right\} ^{2}} \\[ 5pt ]
&=&\frac {3r_{2}E_{2}^{2}\left\{ r_{2}^{2}-\left( sx_{2}\right) ^{2}\right\} }{\left\{ r_{2}^{2}+\left( sx_{2}\right) ^{2}\right\} ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,最大トルクとなる\(s_{\mathrm {m}}\)は\(\displaystyle \frac {\mathrm {d}P_{2}}{\mathrm {d}s}=0\)となる時の値である。よって,
\[
\begin{eqnarray}
\frac {3r_{2}E_{2}^{2}\left\{ r_{2}^{2}-\left( s_{\mathrm {m}}x_{2}\right) ^{2}\right\} }{\left\{ r_{2}^{2}+\left( s_{\mathrm {m}}x_{2}\right) ^{2}\right\} ^{2}}&=& 0 \\[ 5pt ]
r_{2}^{2}-\left( s_{\mathrm {m}}x_{2}\right) ^{2}&=&0 \\[ 5pt ]
r_{2}&=&s_{\mathrm {m}}x_{2} \\[ 5pt ]
s_{\mathrm {m}}&=&\frac {r_{2}}{x_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より\(s_{\mathrm {m}}=0.2\)であるから,\(x_{2}=5r_{2}\)となる。この時,同期ワットで表した最大トルク\(P_{\mathrm {2m}}\)は,
\[
\begin{eqnarray}
P_{\mathrm {2m}}&=& \frac {3s_{\mathrm {m}}r_{2}E_{2}^{2}}{r_{2}^{2}+\left( s_{\mathrm {m}}x_{2}\right) ^{2}} \\[ 5pt ]
&=&\frac {3\cdot 0.2\cdot r_{2}E_{2}^{2}}{r_{2}^{2}+\left( 0.2 \cdot 5r_{2}\right) ^{2}} \\[ 5pt ]
&=&\frac {0.6\cdot r_{2}E_{2}^{2}}{r_{2}^{2}+r_{2}^{2}} \\[ 5pt ]
&=&\frac {0.3E_{2}^{2}}{r_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)二次入力\(P_{2}\),二次銅損\(P_{\mathrm {C2}}\)を,\(E_{2}\)及び\(r_{2}\)で表す
(1)の\(P_{2}\)の式に\(s=0.02\),\(x_{2}=5r_{2}\)を代入すると,
\[
\begin{eqnarray}
P_{2}&=& \frac {3sr_{2}E_{2}^{2}}{r_{2}^{2}+\left( sx_{2}\right) ^{2}} \\[ 5pt ]
&=&\frac {3\cdot 0.02 \cdot r_{2}E_{2}^{2}}{r_{2}^{2}+\left( 0.02\cdot 5r_{2}\right) ^{2}} \\[ 5pt ]
&=&\frac {0.06 \cdot r_{2}E_{2}^{2}}{r_{2}^{2}+0.01r_{2}^{2}} \\[ 5pt ]
&=&\frac {0.06 E_{2}^{2}}{1.01r_{2}} \\[ 5pt ]
&≒&5.9406 \times 10^{-2}\times \frac {E_{2}^{2}}{r_{2}} → 5.94 \times 10^{-2}\times \frac {E_{2}^{2}}{r_{2}}
\end{eqnarray}
\]
と求められる。ワンポイント解説より,二次銅損\(P_{\mathrm {C2}}=sP_{2}\)であるので,
\[
\begin{eqnarray}
P_{\mathrm {C2}}&=& sP_{2} \\[ 5pt ]
&=&0.02 \times 5.9406 \times 10^{-2}\times \frac {E_{2}^{2}}{r_{2}} \\[ 5pt ]
&≒&1.1881\times 10^{-3}\times \frac {E_{2}^{2}}{r_{2}} → 1.19 \times 10^{-3}\times \frac {E_{2}^{2}}{r_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)抵抗\(R_{2}=r_{2}\)を挿入して,同じ一定トルクをもつ負荷を駆動した時の\(s_{2}\)とその時の二次側損失\(P_{\mathrm {w2}}\)
抵抗\(R_{2}=r_{2}\)を挿入した時の電流\(I_{2}^{\prime }\)は,(1)と同様に求めると,
\[
\begin{eqnarray}
I_{2}^{\prime }&=&\frac {s_{2}E_{2}}{\sqrt {\left( R_{2}+r_{2}\right) ^{2}+\left( s_{2}x_{2}\right) ^{2}}} \\[ 5pt ]
&=&\frac {s_{2}E_{2}}{\sqrt {\left( r_{2}+r_{2}\right) ^{2}+\left( 5s_{2}r_{2}\right) ^{2}}}\\[ 5pt ]
&=&\frac {s_{2}E_{2}}{r_{2}\sqrt { 4+25s_{2}^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,二次入力(同期ワットで表したトルク)\(P_{2}^{\prime }\)は,
\[
\begin{eqnarray}
P_{2}^{\prime }&=&3\frac {R_{2}+r_{2}}{s_{2}}{I_{2}^{\prime }}^{2} \\[ 5pt ]
&=&\frac {6r_{2}}{s_{2}}{I_{2}^{\prime }}^{2} \\[ 5pt ]
&=&\frac {6r_{2}}{s_{2}}\left( \frac {s_{2}E_{2}}{r_{2}\sqrt { 4+25s_{2}^{2}}}\right) ^{2} \\[ 5pt ]
&=&\frac {6s_{2}E_{2}^{2}}{\left( 4+25s_{2}^{2}\right) r_{2}}
\end{eqnarray}
\]
となり,題意より,抵抗挿入前後にてトルクは変化しないので,
\[
\begin{eqnarray}
P_{2}&=&P_{2}^{\prime } \\[ 5pt ]
\frac {0.06 E_{2}^{2}}{1.01r_{2}} &=&\frac {6s_{2}E_{2}^{2}}{\left( 4+25s_{2}^{2}\right) r_{2}} \\[ 5pt ]
\frac {6 }{101} &=&\frac {6s_{2}}{4+25s_{2}^{2}} \\[ 5pt ]
25s_{2}^{2}-101s_{2} +4&=&0 \\[ 5pt ]
s_{2}&=&0.04,4 \\[ 5pt ]
\end{eqnarray}
\]
よって,\(0<s_{2}<1\)より,\(s_{2}=0.04\)と求められる。また二次側損失\(P_{\mathrm {w2}}\)は,
\[
\begin{eqnarray}
P_{\mathrm {w2}}&=&s_{2}P_{2}^{\prime } \\[ 5pt ]
&=&s_{2}P_{2} \\[ 5pt ]
&=&0.04\times 5.9406 \times 10^{-2}\times \frac {E_{2}^{2}}{r_{2}}\\[ 5pt ]
&≒&2.3762\times 10^{-3}\times \frac {E_{2}^{2}}{r_{2}} → 2.38 \times 10^{-3}\times \frac {E_{2}^{2}}{r_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)二次励磁電圧\(E_{\mathrm {B}}\),二次銅損\(P^{\prime \prime }_{\mathrm {C2}}\),二次励磁回路へ返還する電力\(P_{\mathrm {B}}\)
回路を流れる二次電流\({\dot I}_{2}^{\prime \prime }\)は,
\[
\begin{eqnarray}
{\dot I}_{2}^{\prime \prime }&=&\frac {sE_{2}-E_{\mathrm {B}}}{r_{2}+\mathrm {j}sx_{2}} \\[ 5pt ]
&=&\frac {sE_{2}-E_{\mathrm {B}}}{r_{2}^{2}+\left( sx_{2}\right) ^{2}}\left( r_{2}-\mathrm {j}sx_{2}\right) \\[ 5pt ]
&=&\frac {0.04E_{2}-E_{\mathrm {B}}}{r_{2}^{2}+\left( 0.04\cdot 5r_{2}\right) ^{2}}\left( r_{2}-\mathrm {j}0.04\cdot 5r_{2}\right) \\[ 5pt ]
&=&\frac {0.04E_{2}-E_{\mathrm {B}}}{1.04 r_{2}}\left( 1-\mathrm {j}0.2\right) \\[ 5pt ]
\end{eqnarray}
\]
であるから,その大きさ\(I_{2}^{\prime \prime }\)は,
\[
\begin{eqnarray}
I_{2}^{\prime \prime }&=&\frac {0.04E_{2}-E_{\mathrm {B}}}{1.04 r_{2}}\sqrt{ 1^{2}+0.2^{2}} \\[ 5pt ]
&=&\frac {0.04E_{2}-E_{\mathrm {B}}}{\sqrt {1.04} r_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,二次入力\(P_{2}^{\prime \prime }\)は,
\[
\begin{eqnarray}
P_{2}^{\prime \prime }&=&\mathrm {Re}\left[ 3{\dot E}_{2}\overline {{\dot I}_{2}^{\prime \prime }}\right] \\[ 5pt ]
&=&\mathrm {Re}\left[ 3E_{2}\frac {0.04E_{2}-E_{\mathrm {B}}}{1.04 r_{2}}\left( 1+\mathrm {j}0.2\right)\right] \\[ 5pt ]
&=&\frac {0.12E_{2}^{2}-3E_{2}E_{\mathrm {B}}}{1.04 r_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。トルクの大きさは(3)から変化しないので,
\[
\begin{eqnarray}
P_{2}^{\prime \prime }&=&P_{2} \\[ 5pt ]
\frac {0.12E_{2}^{2}-3E_{2}E_{\mathrm {B}}}{1.04 r_{2}}&=&\frac {0.06 E_{2}^{2}}{1.01r_{2}} \\[ 5pt ]
\frac {12E_{2}-300E_{\mathrm {B}}}{104 }&=&\frac {6 E_{2}}{101} \\[ 5pt ]
E_{\mathrm {B}}&≒&1.9406\times 10^{-2}E_{2} → 1.94\times 10^{-2}E_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,銅損\(P_{\mathrm {C2}}^{\prime \prime }\)は,
\[
\begin{eqnarray}
P_{\mathrm {C2}}^{\prime \prime }&=&3r_{2}{I_{2}^{\prime \prime }}^{2} \\[ 5pt ]
&=&3r_{2}\left( \frac {0.04E_{2}-E_{\mathrm {B}}}{\sqrt {1.04} r_{2}}\right) ^{2} \\[ 5pt ]
&=&3r_{2}\left( \frac {0.04E_{2}-0.019406E_{2}}{\sqrt {1.04} r_{2}}\right) ^{2} \\[ 5pt ]
&≒&1.2234\times 10^{-3}\times \frac {E_{2}^{2}}{r_{2}} → 1.22 \times 10^{-3}\times \frac {E_{2}^{2}}{r_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。二次励磁回路へ返還する電力\(P_{\mathrm {B}}\)は,
\[
\begin{eqnarray}
P_{\mathrm {B}}&=&\mathrm {Re}\left[ 3{\dot E}_{\mathrm {B}}\overline {{\dot I}_{2}^{\prime \prime }}\right] \\[ 5pt ]
&=&\mathrm {Re}\left[ 3E_{\mathrm {B}}\frac {0.04E_{2}-E_{\mathrm {B}}}{1.04 r_{2}}\left( 1+\mathrm {j}0.2\right)\right] \\[ 5pt ]
&=&\frac {0.12E_{2}E_{\mathrm {B}}-3E_{\mathrm {B}}^{2}}{1.04 r_{2}} \\[ 5pt ]
&=&\frac {0.12E_{2}\cdot 0.019406E_{2}-3\left( 0.019406E_{2}\right) ^{2}}{1.04 r_{2}} \\[ 5pt ]
&≒&1.1528\times 10^{-3}\times \frac {E_{2}^{2}}{r_{2}} → 1.15 \times 10^{-3}\times \frac {E_{2}^{2}}{r_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん