【問題】
【難易度】★★★☆☆(普通)
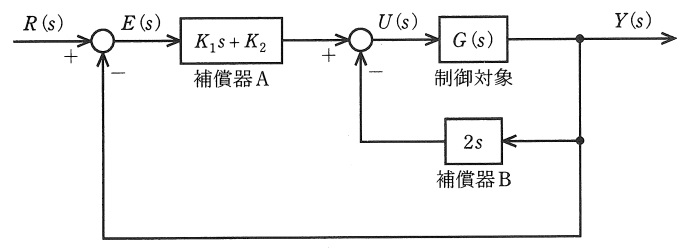
図に示すフィードバック制御系について,次の問に答えよ。ただし,\( \ R\left( s\right) \ \),\( \ E\left( s\right) \ \),\( \ U\left( s\right) \ \),\( \ Y\left( s\right) \ \)は,それぞれ目標値\( \ r\left( t\right) \ \),偏差\( \ e\left( t\right) \ \),入力\( \ u\left( t\right) \ \),出力\( \ y\left( t\right) \ \)をラプラス変換したものであり,\( \ G\left( s\right) \ \)は制御対象の伝達関数を表す。
(1) 図の制御対象\( \ G\left( s\right) \ \)だけを取り出し,大きさ\( \ 1 \ \)のステップ入力を\( \ G\left( s\right) \ \)へ加えたときのステップ応答が次式で与えられるとき,この制御対象の伝達関数\( \ G\left( s\right) \ \)を求めよ。
\[
\begin{cases}
\displaystyle \frac {1}{2}t-\frac {1}{4}+\frac {1}{4}\mathrm {e}^{-2t}, & t≧ 0 \\[ 5pt ]
\displaystyle 0, & t<0 \\[ 5pt ]
\end{cases}
\]
(2) 上記(1)で求めた\( \ G\left( s\right) \ \)とは異なる伝達関数\( \ \displaystyle G\left( s\right) =\frac {1}{s^{2}\left( s+6 \right)} \ \)に置き換えた場合に,図において,目標値\( \ R\left( s\right) \ \)から偏差\( \ E\left( s\right) \ \)までの伝達関数を求めよ。
(3) 上記(2)の制御対象\( \ G\left( s\right) \ \)を含む図のフィードバック制御系の特性根の二つが,\( \ -1+\mathrm {j}\sqrt {3} \ \)と\( \ -1-\mathrm {j}\sqrt {3} \ \)となるように,補償器\( \ \mathrm {A} \ \)のパラメータ\( \ K_{1} \ \)と\( \ K_{2} \ \)を求めよ。さらに,このときの残りの特性根も求めよ。
(4) 上記(2)の制御対象\( \ G\left( s\right) \ \)を含む図のフィードバック制御系において
a. ランプ関数の目標値\( \ r\left( t\right) =t \ \)に対する定常速度偏差の大きさが\( \ \displaystyle \frac {1}{6} \ \)以下
b. フィードバック制御系が安定
の条件を同時に満たす\( \ K_{1} \ \)と\( \ K_{2} \ \)の存在範囲を,横軸\( \ K_{1} \ \),縦軸\( \ K_{2} \ \)のグラフで図示せよ。
【ワンポイント解説】
自動制御の問題は問題慣れすれば,比較的簡単に解けるようになります。
一種では古典制御においてラウスの安定判別式は必須で,よく記憶しておく必要があります。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
u (t) & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\hline
\end{array}
\]
2.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられている時,ラウスの安定判別法による安定条件は,
\[
\begin{eqnarray}
&&1. s^{n},s^{n-1},\cdots ,s^{1},s^{0}の係数がすべて存在 \\[ 5pt ]
&&2. s^{n},s^{n-1},\cdots ,s^{1},s^{0}の係数がすべて同符号 \\[ 5pt ]
&&3. ラウスの数表の値がすべて正であること \\[ 5pt ]
\end{eqnarray}
\]
です。ラウスの数表は下図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & a_{0} & a_{2} & a_{4} & \cdots \\
2行 & a_{1} & a_{3} & a_{5} & \cdots \\
3行 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4行 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
3.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1),大きさ\( \ 1 \ \)のステップ入力を\( \ G\left( s\right) \ \)へ加えたときのこの制御対象の伝達関数\( \ G\left( s\right) \ \)
入力\( \ u\left( t\right) =1 \ \),出力\( \ \displaystyle y\left( t\right) =\frac {1}{2}t-\frac {1}{4}+\frac {1}{4}\mathrm {e}^{-2t} \ \)とし,それぞれラプラス変換すると,
\[
\begin{eqnarray}
U\left( s\right) &=& \frac {1}{s} \\[ 5pt ]
Y\left( s\right) &=& \frac {1}{2s^{2}} -\frac {1}{4s} + \frac {1}{4\left( s+2\right) } \\[ 5pt ]
&=& \frac {1}{s^{2}\left( s+2\right)} \\[ 5pt ]
\end{eqnarray}
\]
となるので,伝達関数\( \ G\left( s\right) \ \)は,
\[
\begin{eqnarray}
G\left( s\right) &=&\frac {Y\left( s\right) }{U\left( s\right) } \\[ 5pt ]
&=&\frac {\displaystyle \frac {1}{s^{2}\left( s+2\right)} }{\displaystyle \frac {1}{s}} \\[ 5pt ]
&=&\frac {1}{s\left( s+2\right)} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)伝達関数\( \ \displaystyle G\left( s\right) =\frac {1}{s^{2}\left( s+6 \right)} \ \)に置き換えた場合の,目標値\( \ R\left( s\right) \ \)から偏差\( \ E\left( s\right) \ \)までの伝達関数
図の伝達関数について,
\[
\begin{eqnarray}
E\left( s\right) &=&R\left( s\right) -Y\left( s\right) &・・・・・・・・・ ①& \\[ 5pt ]
U\left( s\right) &=&\left( K_{1}s+K_{2}\right) E\left( s\right) -2s Y\left( s\right) &・・・・・・・・・ ②& \\[ 5pt ]
Y\left( s\right) &=&\frac {1}{s^{2}\left( s+6\right) }U\left( s\right) &・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
の連立方程式が成り立つ。③から,\( \ U\left( s\right) =s^{2}\left( s+6\right) Y\left( s\right) \ \)であり,これを②に代入すると,
\[
\begin{eqnarray}
s^{2}\left( s+6\right) Y\left( s\right) &=&\left( K_{1}s+K_{2}\right) E\left( s\right) -2s Y\left( s\right) \\[ 5pt ]
\left( s^{3}+6s^{2}+2s\right) Y\left( s\right) &=&\left( K_{1}s+K_{2}\right) E\left( s\right) \\[ 5pt ]
Y\left( s\right)&=&\frac {K_{1}s+K_{2}}{s^{3}+6s^{2}+2s} E\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,これを①に代入すると,
\[
\begin{eqnarray}
E\left( s\right) &=&R\left( s\right) -\frac {K_{1}s+K_{2}}{s^{3}+6s^{2}+2s} E\left( s\right) \\[ 5pt ]
E\left( s\right) +\frac {K_{1}s+K_{2}}{s^{3}+6s^{2}+2s} E\left( s\right) &=&R\left( s\right) \\[ 5pt ]
\frac {s^{3}+6s^{2}+\left( K_{1}+2\right) s+K_{2}}{s^{3}+6s^{2}+2s }E\left( s\right) &=&R\left( s\right) \\[ 5pt ]
\frac {E\left( s\right) }{R\left( s\right) }&=&\frac {s\left( s^{2}+6s+2\right) }{s^{3}+6s^{2}+\left( K_{1}+2\right) s+K_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)パラメータ\( \ K_{1} \ \)と\( \ K_{2} \ \),残りの特性根
特性根は伝達関数\( \ s^{3}+6s^{2}+\left( K_{1}+2\right) s+K_{2}=0 \ \)の根である。残りの特性根を\( \ \alpha \ \)とすると,
\[
\begin{eqnarray}
s^{3}+6s^{2}+\left( K_{1}+2\right) s+K_{2}&=&\left( s-\alpha \right) \left\{ s-\left( -1+\mathrm {j}\sqrt {3}\right) \right\} \left\{ s-\left( -1-\mathrm {j}\sqrt {3}\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
が成立する。右辺を整理すると,
\[
\begin{eqnarray}
s^{3}+6s^{2}+\left( K_{1}+2\right) s+K_{2}&=&\left( s-\alpha \right) \left( s^{2}+2s+4 \right) \\[ 5pt ]
&=&s^{3}+\left( 2-\alpha \right) s^{2}+\left( 4-2\alpha \right) s-4\alpha \\[ 5pt ]
\end{eqnarray}
\]
となり,それぞれの係数を比較すると,
\[
\begin{eqnarray}
2-\alpha &=&6 \\[ 5pt ]
4-2\alpha &=&K_{1}+2 \\[ 5pt ]
-4\alpha &=&K_{2} \\[ 5pt ]
\end{eqnarray}
\]
となるから,\( \ K_{1} \ \),\( \ K_{2} \ \),残りの特性根\( \ \alpha \ \)は,
\[
\begin{eqnarray}
K_{1}=10,K_{2}=16,\alpha =-4 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)a及びbの条件を同時に満たす\( \ K_{1} \ \)と\( \ K_{2} \ \)の存在範囲
aの条件
ランプ関数\( \ r(t)=t \ \)のラプラス変換は,
\[
\begin{eqnarray}
\mathcal{L} \left[ r(t)\right] &=&\mathcal{L} \left[ t\right] \\[ 5pt ]
&=&\frac {1}{s^2} \\[ 5pt ]
\end{eqnarray}
\]
となるから,これを(2)解答式に代入して\( \ E\left( s\right) \ \)を求めると,
\[
\begin{eqnarray}
E\left( s\right) &=&\frac {s\left( s^{2}+6s+2\right) }{s^{3}+6s^{2}+\left( K_{1}+2\right) s+K_{2}} \cdot \frac {1}{s^2} \\[ 5pt ]
&=&\frac {s^{2}+6s+2}{s\left\{ s^{3}+6s^{2}+\left( K_{1}+2\right) s+K_{2}\right\} } \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで最終値の定理より,\( \ \displaystyle \lim_{t \to \infty} e(t) = \displaystyle \lim_{s \to 0} sE(s) \ \)であるから,
\[
\begin{eqnarray}
\lim_{t \to \infty} e(t) &=&\lim_{s \to 0} sE(s) \\[ 5pt ]
&=&\lim_{s \to 0}\left[ \frac {s^{2}+6s+2}{s^{3}+6s^{2}+\left( K_{1}+2\right) s+K_{2}}\right] \\[ 5pt ]
&=&\frac {2}{K_{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,定常速度偏差の大きさが\( \ \displaystyle \frac {1}{6} \ \)であるから,
\[
\begin{eqnarray}
\frac {2}{K_{2}}&≦&\frac {1}{6} \\[ 5pt ]
K_{2}&≧&12 \\[ 5pt ]
\end{eqnarray}
\]
となる。
bの条件
このフィードバック制御系の特性方程式は\( \ s^{3}+6s^{2}+\left( K_{1}+2\right) s+K_{2}=0 \ \)であり,ラウスの数表を作成すると,
\[
\begin{array}{c|cc}
& 1列 & 2列 \\
\hline
1行 & 1 & K_{1}+2 \\
2行 & 6 & K_{2} \\
3行 & \frac {6\left( K_{1}+2\right) -K_{2}}{6} & 0 \\
4行 & K_{2} & \\
\end{array}
\]
となるので,安定となる条件は,
\[
\begin{eqnarray}
K_{1}+2 > 0 &・・・・・・・・・ ④& \\[ 5pt ]
K_{2} > 0 &・・・・・・・・・ ⑤& \\[ 5pt ]
\frac {6\left( K_{1}+2\right) -K_{2}}{6} > 0 &・・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
となる。これより,
\[
\begin{eqnarray}
K_{1} > -2,K_{2} > 0,K_{2}<6K_{1}+12 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
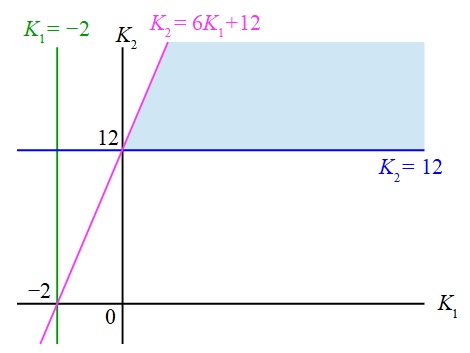
以上から,a及びbを満たす範囲をグラフで表すと,下図に示す範囲となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん