《機械・制御》〈回転機〉[H25:問1] 三相誘導電動機のトルクに関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

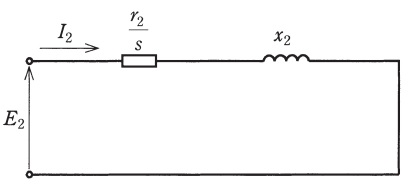
図は，三相誘導電動機の星形換算二次\( \ 1 \ \)相分の等価回路を示す。図中の記号は以下のとおりである。

\( \ E_{2} \ \)：二次誘導起電力\( \ \mathrm {[V]} \ \)，\( \ I_{2} \ \)：二次電流\( \ \mathrm {[A]} \ \)，\( \ s \ \)：滑り
\( \ r_{2} \ \)：二次抵抗\( \ \mathrm {[\Omega ]} \ \)，\( \ x_{2} \ \)：一次周波数における二次リアクタンス\( \ \mathrm {[\Omega ]} \ \)

同期角速度を\( \ \omega _{0} \ \mathrm {[rad/s]} \ \)として，次の問に答えよ。

(1)　\( \ E_{2} \ \)，\( \ r_{2} \ \)，\( \ x_{2} \ \)及び\( \ \omega _{0} \ \)を用いて始動トルク\( \ T_{\mathrm {s}} \ \mathrm {[N\cdot m]} \ \)を表す式を求めよ。

(2)　\( \ T_{\mathrm {s}} \ \)が最大となる\( \ r_{2} \ \)を求めよ。また，そのときのトルク\( \ T_{\mathrm {sm}} \ \mathrm {[N\cdot m]} \ \)を求めよ。

(3)　\( \ r_{2} \ \)は上記(2)で求めた値で，この誘導電動機が滑り\( \ s \ \)で運転されている。このときのトルク\( \ T \ \mathrm {[N\cdot m]} \ \)を上記(2)で求めた\( \ T_{\mathrm {sm}} \ \)及び\( \ s \ \)を用いて表せ。

【ワンポイント解説】

誘導電動機のトルクの導出に関する問題ですが，解くのにも時間があまりかからず近年では最も易しい問題と言えると思います。電験１種二次試験受験者であれば，かなりの方が完答すると思いますので，確実に解けるようにしましょう。

1.電動機のトルク\( \ T \ \)と出力\( \ P_{\mathrm {o}} \ \)の関係
電動機の出力\( \ P_{\mathrm {o}} \ \)は，電動機の角速度\( \ \omega \ \)，トルク\( \ T \ \)とすると，
\[
\begin{eqnarray}
P_{\mathrm {o}}&=&\omega T \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)始動トルク\( \ T_{\mathrm {s}} \ \mathrm {[N\cdot m]} \ \)を表す式
二次電流の大きさ\( \ I_{2} \ \)は，
\[
\begin{eqnarray}
I_{2}&=&\frac {E_{2}}{\sqrt {\left( \displaystyle \frac {r_{2}}{s}\right) ^{2}+x_{2}^{2}}} \\[ 5pt ] \end{eqnarray}
\] となるので，二次入力\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{2}&=&3\left( \frac {r_{2}}{s}\right) I_{2}^{2} \\[ 5pt ] &=&\frac {3\left( \displaystyle \frac {r_{2}}{s}\right)E_{2}^{2}}{\left( \displaystyle \frac {r_{2}}{s}\right) ^{2}+x_{2}^{2}} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「1.電動機のトルク\( \ T \ \)と出力\( \ P_{\mathrm {o}} \ \)の関係」より，
\[
\begin{eqnarray}
T&=&\frac {P}{\omega } \\[ 5pt ] &=&\frac {P_{2}\left( 1-s\right) }{\omega _{0}\left( 1-s\right) } \\[ 5pt ] &=&\frac {P_{2}}{\omega _{0}} \\[ 5pt ] &=&\frac {3\left( \displaystyle \frac {r_{2}}{s}\right)E_{2}^{2}}{\omega _{0}\left[ \left( \displaystyle \frac {r_{2}}{s}\right) ^{2}+x_{2}^{2}\right] } \\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，始動トルクは\( \ s=1 \ \)のトルクであるから，
\[
\begin{eqnarray}
T_{\mathrm {s}}&=&\frac {3r_{2}E_{2}^{2}}{\omega _{0}\left( r_{2}^{2}+x_{2}^{2}\right) } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)\( \ T_{\mathrm {s}} \ \)が最大となる\( \ r_{2} \ \)及びそのときのトルク\( \ T_{\mathrm {sm}} \ \mathrm {[N\cdot m]} \ \)
(1)の解答式の両辺を\( \ r_{2} \ \)で微分すると，
\[
\begin{eqnarray}
\frac {\mathrm {d}T_{\mathrm {s}}}{\mathrm {d}r_{2}}&=&\frac {3E_{2}^{2}\omega _{0}\left( r_{2}^{2}+x_{2}^{2}\right) -3r_{2}E_{2}^{2}\omega _{0}\cdot 2r_{2}}{\left[ \omega _{0}\left( r_{2}^{2}+x_{2}^{2}\right) \right] ^{2}} \\[ 5pt ] &=&\frac {3E_{2}^{2}}{\omega _{0}}\frac {\left( r_{2}^{2}+x_{2}^{2}\right) -2r_{2}^{2}}{\left( r_{2}^{2}+x_{2}^{2}\right) ^{2}} \\[ 5pt ] &=&\frac {3E_{2}^{2}}{\omega _{0}}\frac {x_{2}^{2}-r_{2}^{2}}{\left( r_{2}^{2}+x_{2}^{2}\right) ^{2}} \\[ 5pt ] &=&\frac {3E_{2}^{2}}{\omega _{0}}\frac {\left( x_{2}-r_{2}\right) \left( x_{2}+r_{2}\right) }{\left( r_{2}^{2}+x_{2}^{2}\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となる。トルクが最大となるとき\( \ \displaystyle \frac {\mathrm {d}T_{\mathrm {s}}}{\mathrm {d}r_{2}}=0 \ \)であるから，\( \ r_{2}=x_{2} \ \)となる。
また，この時のトルク\( \ T_{\mathrm {sm}} \ \)は，
\[
\begin{eqnarray}
T_{\mathrm {sm}}&=&\frac {3r_{2}E_{2}^{2}}{\omega _{0}\left( r_{2}^{2}+r_{2}^{2}\right) } \\[ 5pt ] &=&\frac {3E_{2}^{2}}{2\omega _{0}r_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)\( \ r_{2} \ \)は上記(2)で求めた値で，この誘導電動機が滑り\( \ s \ \)で運転されているときのトルク\( \ T \ \mathrm {[N\cdot m]} \ \)
トルクは，
\[
\begin{eqnarray}
T&=&\frac {3\left( \displaystyle \frac {r_{2}}{s}\right)E_{2}^{2}}{\omega _{0}\left[ \left( \displaystyle \frac {r_{2}}{s}\right) ^{2}+x_{2}^{2}\right] } \\[ 5pt ] \end{eqnarray}
\] であるから，\( \ r_{2}=x_{2} \ \)を代入すると，
\[
\begin{eqnarray}
T&=&\frac {3\left( \displaystyle \frac {r_{2}}{s}\right)E_{2}^{2}}{\omega _{0}\left[ \left( \displaystyle \frac {r_{2}}{s}\right) ^{2}+r_{2}^{2}\right] } \\[ 5pt ] &=&\frac {3E_{2}^{2}}{\omega _{0}r_{2}}\frac {\displaystyle \frac {1}{s}}{\left[ \left( \displaystyle \frac {1}{s}\right) ^{2}+1\right] } \\[ 5pt ] &=&2T_{\mathrm {sm}}\frac {s}{1+s^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。