【問題】
【難易度】★★★☆☆(普通)
三相星形結線の円筒形同期発電機\( \ \mathrm {A} \ \)機及び\( \ \mathrm {B} \ \)機の\( \ 2 \ \)台が共通母線に接続され並列運転している。\( \ \mathrm {A} \ \)機は定格容量\( \ 8000 \ \mathrm {[kV\cdot A]} \ \),定格電圧(線間電圧)\( \ 6600 \ \mathrm {[V]} \ \),定格力率\( \ 0.9 \ \)(遅れ),同期リアクタンス\( \ 1.7 \ \mathrm {[p.u.]} \ \)であり,\( \ \mathrm {B} \ \)機は定格容量\( \ 10000 \ \mathrm {[kV\cdot A]} \ \),定格電圧(線間電圧)\( \ 6600 \ \mathrm {[V]} \ \),定格力率\( \ 0.9 \ \)(遅れ),同期リアクタンス\( \ 1.7 \ \mathrm {[p.u.]} \ \)である。この並列運転に関して次の問に答えよ。ただし,鉄心の磁気飽和及び電機子抵抗は無視できるものとする。また,単位法は各機の定格容量を基準としている。
(1) 両機が母線電圧(線間電圧)\( \ 6600 \ \mathrm {[V]} \ \)で並列運転して,\( \ 12000 \ \mathrm {[kW]} \ \)遅れ力率\( \ 0.9 \ \)の負荷を負っている。両機が\( \ 6000 \ \mathrm {[kW]} \ \)ずつ負荷電力を分担するように調整したとき,\( \ \mathrm {A} \ \)機の運転力率は\( \ 0.95 \ \)(遅れ)であった。
a. 負荷電流\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \),両機の電機子電流\( \ I_{\mathrm {A}} \ \mathrm {[A]} \ \),\( \ I_{\mathrm {B}} \ \mathrm {[A]} \ \),及び\( \ \mathrm {B} \ \)機の運転力率\( \ \cos \mathit {\phi }_{\mathrm {B}} \ \)を求めよ。
b. 両機の同期リアクタンス\( \ X_{\mathrm {A}} \ \mathrm {[\Omega ]} \ \),\( \ X_{\mathrm {B}} \ \mathrm {[\Omega ]} \ \),及び無負荷誘導起電力(相電圧)\( \ E_{\mathrm {A}} \ \mathrm {[V]} \ \),\( \ E_{\mathrm {B}} \ \mathrm {[V]} \ \)を求めよ。
(2) 上記(1)において,母線電圧(線間電圧)\( \ 6600 \ \mathrm {[V]} \ \)のままで,徐々に負荷状態が変化して,両機は並列運転にて\( \ 15000 \ \mathrm {[kW]} \ \)の負荷電力を負うことになった。この負荷電力に対して,両機の無負荷誘導起電力\( \ E_{\mathrm {A}} \ \),\( \ E_{\mathrm {B}} \ \)を上記(1)b.の値に保ちながら,各機の負荷電力を徐々に変えると,同期化力によって\( \ E_{\mathrm {A}} \ \),\( \ E_{\mathrm {B}} \ \)は同位相になった。このときの\( \ E_{\mathrm {A}} \ \),\( \ E_{\mathrm {B}} \ \)と母線の相電圧との内部相差角を\( \ \delta \ \mathrm {[rad]} \ \)として,その\( \ \sin \delta \ \)及びそのときの各機が分担する有効電力\( \ \mathrm {[kW]} \ \)を求めよ。
【ワンポイント解説】
同期発電機の平衡運転に関する問題です。単位法を用いて解くか迷う問題ですが,本問の場合,単位法を使わず普通に解いた方が速そうなので,そちらを採用しました。
1.単位法
基準容量を\( \ P_{\mathrm {B}} \ \),基準電圧を\( \ V_{\mathrm {B}} \ \)とすると,
\[
\begin{eqnarray}
P \ \mathrm {[p.u.]}&=&\frac {P \ \mathrm {[W]}}{P_{\mathrm {B}}} \\[ 5pt ]
V \ \mathrm {[p.u.]}&=&\frac {V \ \mathrm {[V]}}{V_{\mathrm {B}}} \\[ 5pt ]
I \ \mathrm {[p.u.]}&=&\frac {I \ \mathrm {[A]}}{I_{\mathrm {B}}} \\[ 5pt ]
&=&\frac {I \ \mathrm {[A]}}{\displaystyle \frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}}} \\[ 5pt ]
&=&\frac {\sqrt {3}V_{\mathrm {B}}}{P_{\mathrm {B}}}\cdot I \ \mathrm {[A]} \\[ 5pt ]
Z \ \mathrm {[p.u.]}&=&\frac {Z \ \mathrm {[\Omega ]}}{Z_{\mathrm {B}}} \\[ 5pt ]
&=&\frac {Z \ \mathrm {[\Omega ]}}{\displaystyle \frac {V_{\mathrm {B}}}{\sqrt {3}I_{\mathrm {B}}}} \\[ 5pt ]
&=&\frac {\sqrt {3}}{V_{\mathrm {B}}}I_{\mathrm {B}}\cdot Z \ \mathrm {[\Omega ]} \\[ 5pt ]
&=&\frac {\sqrt {3}}{V_{\mathrm {B}}} \frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}}\cdot Z \ \mathrm {[\Omega ]} \\[ 5pt ]
&=&\frac {P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}}\cdot Z \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となります。インピーダンスの式は公式として暗記しておきましょう。
【解答】
(1)a.負荷電流\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \),両機の電機子電流\( \ I_{\mathrm {A}} \ \mathrm {[A]} \ \),\( \ I_{\mathrm {B}} \ \mathrm {[A]} \ \),\( \ \cos \mathit {\phi }_{\mathrm {B}} \ \)をを求める
題意の内容を図に整理すると,図1のようになる。各記号は図1のようにおく。
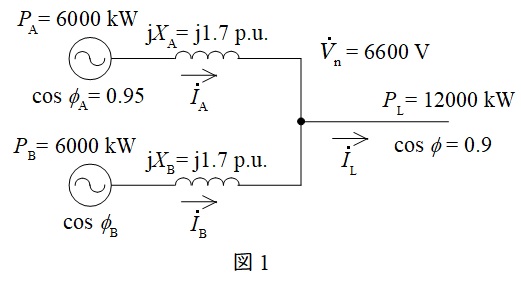
負荷の電力\( \ P_{\mathrm {L}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {L}}\cos \phi \ \)より,負荷電流\( \ I_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {L}}&=&\frac {P_{\mathrm {L}}}{\sqrt {3}V_{\mathrm {n}}\cos \mathit {\phi } } \\[ 5pt ]
&=&\frac {12000\times 10^{3}}{\sqrt {3}\times 6600 \times 0.9 } \\[ 5pt ]
&≒&1166.4 → 1170 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ \mathrm {A} \ \)機の電機子電流\( \ I_{\mathrm {A}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {A}}&=&\frac {P_{\mathrm {A}}}{\sqrt {3}V_{\mathrm {n}}\cos \mathit {\phi } _{\mathrm {A}} } \\[ 5pt ]
&=&\frac {6000\times 10^{3}}{\sqrt {3}\times 6600 \times 0.95 } \\[ 5pt ]
&≒&552.49 → 552 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。ここで,各電流をベクトル式で表すと,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {L}}&=&I_{\mathrm {L}}\cos \mathit {\phi } -\mathrm {j}I_{\mathrm {L}}\sin \mathit {\phi } \\[ 5pt ]
&=&1166.4\times 0.9 -\mathrm {j}1166.4\times \sqrt {1-0.9^{2}} \\[ 5pt ]
&≒&1049.8-\mathrm {j}508.42 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
{\dot I}_{\mathrm {A}}&=&I_{\mathrm {A}}\cos \mathit {\phi } _{\mathrm {A}}-\mathrm {j}I_{\mathrm {A}}\sin \mathit {\phi } _{\mathrm {A}} \\[ 5pt ]
&=&552.49\times 0.95 -\mathrm {j}552.49\times \sqrt {1-0.95^{2}} \\[ 5pt ]
&≒&524.87-\mathrm {j}172.51 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \mathrm {B} \ \)機の電機子電流\( \ {\dot I}_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {B}}&=&{\dot I}_{\mathrm {L}}-{\dot I}_{\mathrm {A}} \\[ 5pt ]
&=&1049.8-\mathrm {j}508.42-\left( 524.87-\mathrm {j}172.51\right) \\[ 5pt ]
&≒&524.93-\mathrm {j}335.91 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさは,
\[
\begin{eqnarray}
I_{\mathrm {B}}&=&\sqrt {524.93^{2}+335.91^{2}} \\[ 5pt ]
&≒&623.21 → 623 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ \mathrm {B} \ \)機の運転力率\( \ \cos \mathit {\phi }_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
\cos \mathit {\phi }_{\mathrm {B}}&=&\frac {524.93}{623.21} \\[ 5pt ]
&≒&0.84230 → 0.842(遅れ) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(1)b. 両機の同期リアクタンス\( \ X_{\mathrm {A}} \ \mathrm {[\Omega ]} \ \),\( \ X_{\mathrm {B}} \ \mathrm {[\Omega ]} \ \),及び無負荷誘導起電力(相電圧)\( \ E_{\mathrm {A}} \ \mathrm {[V]} \ \),\( \ E_{\mathrm {B}} \ \mathrm {[V]} \ \)を求める
ワンポイント解説「1.単位法」より,
\[
\begin{eqnarray}
X_{\mathrm {A}} \ \mathrm {[\Omega ]}&=&\frac {V_{\mathrm {n}}^{2}}{P_{\mathrm {A}}}\cdot X_{\mathrm {A}} \ \mathrm {[p.u.]} \\[ 5pt ]
&=&\frac {6600^{2}}{8000\times 10^{3}}\times 1.7 \\[ 5pt ]
&=&9.2565 → 9.26 \ \mathrm {[\Omega ]} \\[ 5pt ]
X_{\mathrm {B}} \ \mathrm {[\Omega ]}&=&\frac {V_{\mathrm {n}}^{2}}{P_{\mathrm {B}}}\cdot X_{\mathrm {A}} \ \mathrm {[p.u.]} \\[ 5pt ]
&=&\frac {6600^{2}}{10000\times 10^{3}}\times 1.7 \\[ 5pt ]
&=&7.4052 → 7.41 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。無負荷誘導起電力\( \ {\dot E}_{\mathrm {A}} \ \),\( \ {\dot E}_{\mathrm {B}} \ \)は,図1より,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {A}}&=&\frac {{\dot V}_{\mathrm {n}}}{\sqrt {3}}+\mathrm {j} X_{\mathrm {A}} {\dot I}_{\mathrm {A}} \\[ 5pt ]
&=&\frac {6600}{\sqrt {3}}+\mathrm {j} \times 9.2565 \times \left( 524.87-\mathrm {j}172.51\right) \\[ 5pt ]
&=&5407.4+\mathrm {j} 4858.5 \\[ 5pt ]
{\dot E}_{\mathrm {B}}&=&\frac {{\dot V}_{\mathrm {n}}}{\sqrt {3}}+\mathrm {j} X_{\mathrm {B}} {\dot I}_{\mathrm {B}} \\[ 5pt ]
&=&\frac {6600}{\sqrt {3}}+\mathrm {j} \times 7.4052 \times \left( 524.93-\mathrm {j}335.91\right) \\[ 5pt ]
&=&6298.0+\mathrm {j} 3887.2 \\[ 5pt ]
\end{eqnarray}
\]
となるので,それぞれの大きさ\( \ E_{\mathrm {A}} \ \),\( \ E_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {A}}&=&\sqrt {5407.4^{2}+4858.5^{2}} \\[ 5pt ]
&=&7269.5 → 7270 \ \mathrm {[V]} \\[ 5pt ]
E_{\mathrm {B}}&=&\sqrt {6298.0^{2}+3887.2^{2}} \\[ 5pt ]
&=&7401.0 → 7400 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ \sin \delta \ \)及び各機が分担する有効電力\( \ \mathrm {[kW]} \ \)
題意に沿ってベクトル図を描くと図2のようになる。
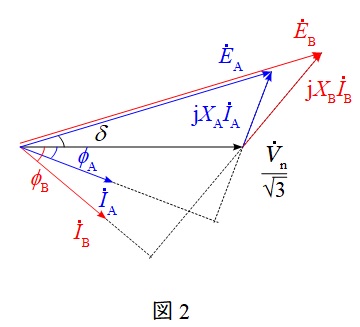
図2より,
\[
\begin{eqnarray}
E_{\mathrm {A}}\sin \delta &=&X_{\mathrm {A}}I_{\mathrm {A}}\cos \mathit {\phi }_{\mathrm {A}} & ・・・・・・・・・①& \\[ 5pt ]
E_{\mathrm {B}}\sin \delta &=&X_{\mathrm {B}}I_{\mathrm {B}}\cos \mathit {\phi }_{\mathrm {B}} & ・・・・・・・・・②& \\[ 5pt ]
\end{eqnarray}
\]
であり,それぞれの電力\( \ P_{\mathrm {A}} \ \),\( \ P_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {A}}&=&\sqrt {3}V_{\mathrm {n}}I_{\mathrm {A}}\cos \mathit {\phi }_{\mathrm {A}} \\[ 5pt ]
I_{\mathrm {A}}\cos \mathit {\phi }_{\mathrm {A}}&=&\frac {P_{\mathrm {A}}}{\sqrt {3}V_{\mathrm {n}}} & ・・・・・・・・・③& \\[ 5pt ]
P_{\mathrm {B}}&=&\sqrt {3}V_{\mathrm {n}}I_{\mathrm {B}}\cos \mathit {\phi }_{\mathrm {B}} \\[ 5pt ]
I_{\mathrm {B}}\cos \mathit {\phi }_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {n}}} & ・・・・・・・・・④& \\[ 5pt ]
\end{eqnarray}
\]
となる。③,④を①,②にそれぞれ代入すると,
\[
\begin{eqnarray}
E_{\mathrm {A}}\sin \delta &=&X_{\mathrm {A}}\frac {P_{\mathrm {A}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ]
P_{\mathrm {A}}&=&\frac {\sqrt {3}E_{\mathrm {A}}V_{\mathrm {n}}}{X_{\mathrm {A}}}\sin \delta \\[ 5pt ]
E_{\mathrm {B}}\sin \delta &=&X_{\mathrm {B}}\frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ]
P_{\mathrm {B}}&=&\frac {\sqrt {3}E_{\mathrm {B}}V_{\mathrm {n}}}{X_{\mathrm {B}}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ P_{\mathrm {A}}+P_{\mathrm {B}}=15000 \ \mathrm {[kW]} \ \)であるから,
\[
\begin{eqnarray}
\frac {\sqrt {3}E_{\mathrm {A}}V_{\mathrm {n}}}{X_{\mathrm {A}}}\sin \delta +\frac {\sqrt {3}E_{\mathrm {B}}V_{\mathrm {n}}}{X_{\mathrm {B}}}\sin \delta &=&15000\times 10^{3} \\[ 5pt ]
\sin \delta &=&\frac {1}{\displaystyle \frac {\sqrt {3}E_{\mathrm {A}}V_{\mathrm {n}}}{X_{\mathrm {A}}}+\frac {\sqrt {3}E_{\mathrm {B}}V_{\mathrm {n}}}{X_{\mathrm {B}}}}\times 15000\times 10^{3} \\[ 5pt ]
\end{eqnarray}
\]
となるので,各値を代入すると,
\[
\begin{eqnarray}
\sin \delta &=&\frac {1}{\displaystyle \frac {\sqrt {3}E_{\mathrm {A}}V_{\mathrm {n}}}{X_{\mathrm {A}}}+\frac {\sqrt {3}E_{\mathrm {B}}V_{\mathrm {n}}}{X_{\mathrm {B}}}}\times 15000\times 10^{3} \\[ 5pt ]
&=&\frac {1}{\displaystyle \frac {\sqrt {3}\times 7269.5\times 6600}{9.2565}+\frac {\sqrt {3}\times 7401.0\times 6600}{7.4052}}\times 15000\times 10^{3} \\[ 5pt ]
&≒&0.73520 → 0.735 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,各機が分担する有効電力は,
\[
\begin{eqnarray}
P_{\mathrm {A}}&=&\frac {\sqrt {3}E_{\mathrm {A}}V_{\mathrm {n}}}{X_{\mathrm {A}}}\sin \delta \\[ 5pt ]
&=&\frac {\sqrt {3}\times 7269.5\times 6600}{9.2565}\times 0.73520 \\[ 5pt ]
&≒&6600362 \ \mathrm {[W]} → 6600 \ \mathrm {[kW]} \\[ 5pt ]
P_{\mathrm {B}}&=&P_{\mathrm {L}}-P_{\mathrm {A}} \\[ 5pt ]
&=&15000-6600 \\[ 5pt ]
&=&8400 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん