《機械・制御》〈回転機〉[H27:問2] 円筒形同期発電機における出力と界磁電流との関係に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

三相星形結線の円筒形同期発電機(短絡比$0.5$ )における出力と界磁電流との関係に関して，次の問に答えよ。ただし，鉄心の磁気飽和及び電機子抵抗は無視する。また，単位法は自己定格容量(定格皮相電力$\mathrm {[kV\cdot A]}$)を基準としている。なお，界磁電流$I_{\mathrm {f}}$の大きさは，無負荷状態で定格電圧発生時の界磁電流$I_{\mathrm {f0}}$に対する比$k_{\mathrm {1F}}$( $\displaystyle k_{\mathrm {1F}}=\frac {I_{\mathrm {f}}}{I_{\mathrm {f0}}}$ )で表示する。

(1)　定格周波数における，単位法表示の同期リアクタンス$X_{\mathrm {S}} \ \mathrm {[ p.u. ]}$の数値を算出せよ。

(2)　端子電圧(相電圧)$V \ \mathrm {[ p.u. ]}$，無負荷誘導起電力$E \ \mathrm {[ p.u. ]}$，負荷角(内部相差角)$\delta \ \mathrm {[ p.u. ]}$及び$X_{\mathrm {S}} \ \mathrm {[ p.u. ]}$を含む有効電力$P \ \mathrm {[ p.u. ]}$の式を導出せよ。また，$V$及び周波数が一定で運転し，$P$が一定の状態において$I_{\mathrm {f}}$を変化させても$E\sin \delta$が一定であることを示せ。

(3)　$V \ \mathrm {[ p.u. ]}$，$E \ \mathrm {[ p.u. ]}$，$\delta \ \mathrm {[ p.u. ]}$及び$X_{\mathrm {S}} \ \mathrm {[ p.u. ]}$を含む無効電力$Q \ \mathrm {[ p.u. ]}$の式(誘導性無効電力を出力する遅れ力率のとき，$Q ＞ 0$とする)を導出せよ。また，$V$及び周波数が一定で運転し，$Q$が一定の状態において$I_{\mathrm {f}}$を変化させても$E\cos \delta$が一定であることを示せ。

(4)　定格周波数において，$\ V =1 \ \mathrm { p.u. } \ $及び$\ P =0.5 \ \mathrm { p.u. } \ $一定の状態で$I_{\mathrm {f}}$の大きさを$k_{\mathrm {1F}}=2$にしたときの$Q \ \mathrm {[ p.u. ]}$，$E \ \mathrm {[ p.u. ]}$，出力電流(相電流)$I \ \mathrm {[ p.u. ]}$及び力率$\cos \phi$の数値を算出せよ。ただし，$\displaystyle 0 ≦ \delta ≦ \frac {\pi}{2} \mathrm {rad}$とする。

【ワンポイント解説】

一種としては比較的易しい問題に分類されると思います。等価回路とベクトル図を描いて落ち着いて解くようにしましょう。

1.同期電動機の特性曲線
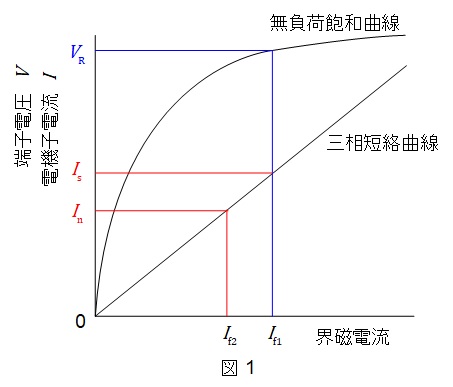
同期電動機の特性曲線は図1のように描けられ，短絡比$K_{\mathrm {s}}$は次のように定義されます。
$$\begin{eqnarray} K_{\mathrm {s}} &=& \frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ] &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ] \end{eqnarray}$$ 短絡比$K_{\mathrm {s}}$と単位法で表した同期インピーダンス$Z_{\mathrm {s}}$との関係は，
$$\begin{eqnarray} K_{\mathrm {s}} &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ] &=& \frac {\frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}}}}{I_{\mathrm {n}}} \\[ 5pt ] &=& \frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}}I_{\mathrm {n}}}\\[ 5pt ] &=& \frac {1}{Z_{\mathrm {s}}\mathrm {[p.u.]}} \\[ 5pt ] \end{eqnarray}$$ となります。

【解答】

(1)単位法表示の同期リアクタンス$X_{\mathrm {S}} \ \mathrm {[ p.u. ]}$
電機子抵抗を無視できるので，ワンポイント解説「1.同期電動機の特性曲線」より，
$$\begin{eqnarray} X_{\mathrm {s}}\mathrm {[p.u.]} &=& \frac {1}{K_{\mathrm {s}}} \\[ 5pt ] &=& \frac {1}{0.5} \\[ 5pt ] &=& 2 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(2)有効電力$P \ \mathrm {[ p.u. ]}$の式を導出，$E\sin \delta$が一定であることを示す
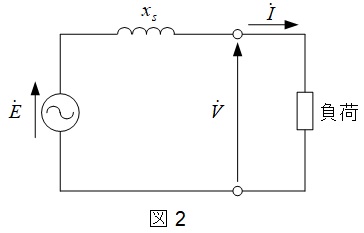
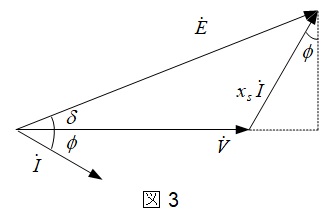
力率を$\cos \phi$として，題意に沿って等価回路とベクトル図を描くと図2及び図3の通りとなる。
図3のベクトル図より，
$$\begin{eqnarray} E\sin \delta &=& X_{\mathrm {s}}I\cos \phi \\[ 5pt ] I\cos \phi &=& \frac {E\sin \delta }{X_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}$$ となり，$P=VI\cos \phi$であるので，
$$\begin{eqnarray} P &=& VI\cos \phi \\[ 5pt ] &=& \frac {EV\sin \delta }{X_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}$$ と求められる。これより，
$$\begin{eqnarray} E\sin \delta &=& \frac {PX_{\mathrm {s}}}{V} \\[ 5pt ] \end{eqnarray}$$ となり，周波数が一定であれば$X_{\mathrm {s}}$も一定であり，$P$及び$V$も一定なので，$E\sin \delta$も一定となる。

(3)無効電力$Q \ \mathrm {[ p.u. ]}$の式を導出，$E\cos \delta$が一定であることを示す
図3のベクトル図より，
$$\begin{eqnarray} E\cos \delta &=& V+X_{\mathrm {s}}I\sin \phi \\[ 5pt ] I\sin \phi &=& \frac {E\cos \delta -V}{X_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}$$ となり，$Q=VI\sin \phi$であるので，
$$\begin{eqnarray} Q &=& VI\sin \phi \\[ 5pt ] &=& V\cdot \frac {E\cos \delta -V}{X_{\mathrm {s}}} \\[ 5pt ] &=& \frac {EV\cos \delta -V^{2}}{X_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}$$ と求められる。これより，
$$\begin{eqnarray} EV\cos \delta -V^{2} &=& QX_{\mathrm {s}} \\[ 5pt ] E\cos \delta &=& \frac {QX_{\mathrm {s}}}{V}+V \\[ 5pt ] \end{eqnarray}$$ となり，周波数が一定であれば$X_{\mathrm {s}}$も一定であり，$Q$及び$V$も一定なので，$E\cos \delta$も一定となる。

(4)$Q \ \mathrm {[ p.u. ]}$，$E \ \mathrm {[ p.u. ]}$，出力電流(相電流)$I \ \mathrm {[ p.u. ]}$及び力率$\cos \phi$の数値を算出
$E ∝ I_{\mathrm {f}}$であるから，$E=2.0 \ \mathrm {[ p.u. ]}$となる。
(2)より，
$$\begin{eqnarray} P &=& \frac {EV\sin \delta }{X_{\mathrm {s}}} \\[ 5pt ] 0.5 &=& \frac {2\times 1 \times \sin \delta }{2} \\[ 5pt ] \sin \delta &=& \frac {1}{2} \end{eqnarray}$$ となるから，$\displaystyle \cos \delta =\frac {\sqrt {3}}{2}$となるので，
$$\begin{eqnarray} Q &=& \frac {EV\cos \delta -V^{2}}{X_{\mathrm {s}}} \\[ 5pt ] &=& \frac {2\times 1 \times \frac {\sqrt {3}}{2} -1}{2} \\[ 5pt ] &≒& 0.36603　→　0.366 \ \mathrm {[ p.u. ]} \\[ 5pt ] \end{eqnarray}$$ と求められる。$P$及び$Q$より，
$$\begin{eqnarray} \cos \phi &=& \frac {P}{\sqrt {P^{2}+Q^{2}}} \\[ 5pt ] &=& \frac {0.5}{\sqrt {0.5^{2}+0.36603^{2}}} \\[ 5pt ] &≒& 0.80689　→　0.807 \ \mathrm {[ p.u. ]} \\[ 5pt ] \end{eqnarray}$$ と求められる。$P=VI\cos \phi$であるから，
$$\begin{eqnarray} I &=& \frac {P}{V\cos \phi } \\[ 5pt ] &=& \frac {0.5}{1\times 0.80689 } \\[ 5pt ] &≒& 0.61966　→　0.620 \ \mathrm {[ p.u. ]} \\[ 5pt ] \end{eqnarray}$$ と求められる。