【問題】
【難易度】★★★☆☆(普通)
定格容量\( \ 15 \ 000 \ \mathrm {kV\cdot A} \ \),定格一次電圧\( \ 66 \ \mathrm {kV} \ \),定格二次電圧\( \ 11 \ \mathrm {kV} \ \)の単相変圧器があり,試験結果は次のとおりであった。
・高圧側(一次側)を開放して無負荷試験を行った場合:
電圧\( \ V_{\mathrm {20}}=11 \ 000 \ \mathrm {V} \ \),電流\( \ I_{\mathrm {20}}=44 \ \mathrm {A} \ \),電力\( \ P_{\mathrm {20}}=55 \ \mathrm {kW} \ \)
・高圧側(一次側)を短絡して短絡試験を行った場合:
電圧\( \ V_{\mathrm {2s}}=660 \ \mathrm {V} \ \),電流\( \ I_{\mathrm {2s}}=1 \ 364 \ \mathrm {A} \ \),電力\( \ P_{\mathrm {2s}}=110 \ \mathrm {kW} \ \)
次の問に答えよ。
ただし,定格容量の負荷時の力率\( \ \cos \theta \ \)における電圧の変動率\( \ \varepsilon \ \mathrm {[%]} \ \)は,百分率抵抗降下を\( \ p \ \mathrm {[%]} \ \),百分率リアクタンス降下を\( \ q \ \mathrm {[%]} \ \)とすれば,次式で表せるものとする。
\[
\begin{eqnarray}
\varepsilon &=&p\cos \theta +q\sin \theta +\frac {1}{200}\left( q\cos \theta -p\sin \theta \right) ^{2} \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
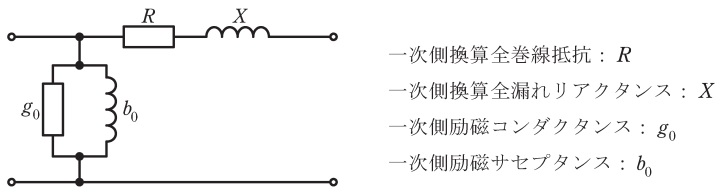
(1) 図に示す一次側から見た簡易等価回路の回路定数をそれぞれ求めよ。ただし,上記無負荷試験においては巻線抵抗と漏れリアクタンスによる電圧降下を,短絡試験においては鉄損を無視できるものとする。
(2) 百分率抵抗降下\( \ p \ \mathrm {[%]} \ \),百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)及び百分率インピーダンス\( \ z \ \mathrm {[%]} \ \)を求めよ。
(3) 遅れ力率\( \ 80 \ \mathrm {%} \ \)で定格容量の負荷における電圧の変動率\( \ \varepsilon \ \mathrm {[%]} \ \)を求めよ。
(4) 力率\( \ 100 \ \mathrm {%} \ \)において効率が最大のとき,負荷電力\( \ P_{\mathrm {L}} \ \mathrm {[kW]} \ \)及び最大効率\( \ \eta _{\mathrm {m}} \ \mathrm {[%]} \ \)を求めよ。
【ワンポイント解説】
変圧器の短絡試験や無負荷試験に関する問題です。
\( \ 3 \ \)種の頃から扱う内容なので,\( \ 1 \ \)種受験生であれば一度は学習したことがある内容かと思います。ただし,計算量が非常に多い問題なので,本番で選択するかどうかはよく検討しましょう。本問で与えられている電圧変動率の式は過去与えられなかったこともあるので,覚えておくようにしましょう。
1.変圧器の\( \ \mathrm {L} \ \)形簡易等価回路(一次換算)
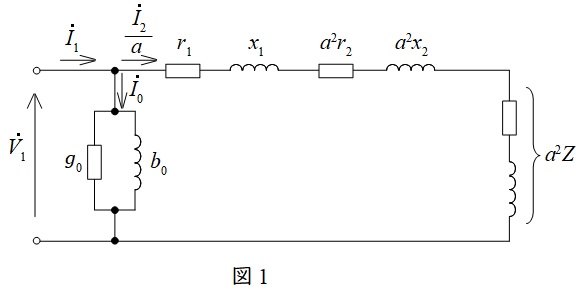
変圧器の一次側等価回路を図1に示します。ただし,\( \ {\dot V}_{1} \ \)は一次側端子電圧,\( \ {\dot I}_{1} \ \)は一次電流,\( \ {\dot I}_{2} \ \)は二次電流,\( \ {\dot I}_{0} \ \)は励磁電流,\( \ r_{1} \ \)は一次巻線抵抗,\( \ r_{2} \ \)は二次巻線抵抗,\( \ x_{1} \ \)は一次漏れリアクタンス,\( \ x_{2} \ \)は二次漏れリアクタンス,\( \ a \ \)は変圧比(巻数比)となります。
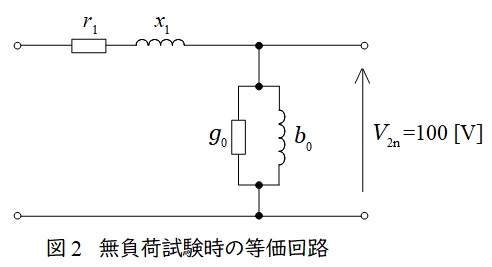
2.無負荷試験の等価回路
変圧器の無負荷試験は一次側を開放して,二次側に定格電圧を加える試験です。測定される電力は鉄損となり,測定される電力と電流から,励磁コンダクタンス\( \ g_{0} \ \)及び励磁サセプタンス\( \ b_{0} \ \)を求めることが可能となります。二次側に定格電圧を加えるのが一般的ですが,二次側開放で一次側に定格電圧を加えても同様に求められます。
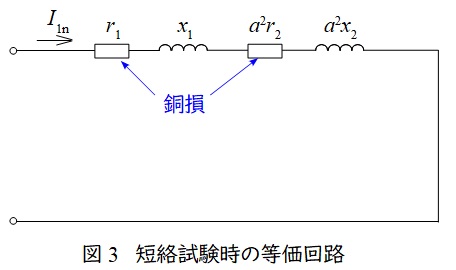
3.短絡試験の等価回路
変圧器の短絡試験は二次側を短絡して,一次側にインピーダンス電圧を加えて,定格電流を流す試験です。励磁回路に流れる電流が十分に小さいと仮定すると,測定される電力は銅損となります。測定される電力と電流から,高圧側換算の巻線抵抗\( \ R=r_{1}+a^{2}r_{2} \ \)を求めることが可能となります。変圧器一次側を短絡しても求めることが可能となりますが,その場合は二次側換算の巻線抵抗が求められます。
4.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)
変圧器の損失は鉄損\( \ p_{\mathrm {i}} \ \)と銅損\( \ p_{\mathrm {c}} \ \)があり,\( \ p_{\mathrm {i}} \ \)は負荷によらず一定であり,\( \ p_{\mathrm {c}} \ \)は負荷(電流)の\( \ 2 \ \)乗に比例します。従って,力率が\( \ 1 \ \)の負荷を接続したとき,定格出力\( \ P_{\mathrm {n}} \ \)で利用率\( \ \alpha \ \)の時の変圧器の効率\( \ \eta \ \)は,
\[
\begin{eqnarray}
\eta &=&\frac {出力}{入力} \\[ 5pt ]
&=&\frac {出力}{出力+損失} \\[ 5pt ]
&=&\frac {\alpha P_{\mathrm {n}}}{\alpha P_{\mathrm {n}}+p_{\mathrm {i}}+\alpha ^{2}p_{\mathrm {c}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
次に,最大効率\( \ \eta _{\mathrm {m}} \ \)を求めます。上式の分母分子を\( \ \alpha \ \)で割ると
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {n}}}{\displaystyle P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,効率が最大となるためには,上式の分母が最小となれば良いので,\( \ \displaystyle A=P_{\mathrm {n}}+\frac {p_{\mathrm {i}}}{\alpha }+\alpha p_{\mathrm {c}} \ \)と置くと,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}\alpha }&=&-\frac {p_{\mathrm {i}}}{\alpha ^{2} }+p_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となります。よって\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}\alpha }=0 \ \)となるとき,\( \ p_{\mathrm {i}}=\alpha ^{2}p_{\mathrm {c}} \ \)であり,鉄損と銅損が等しい時効率は最大となります。
※ 本問題を解く上では,鉄損と銅損が等しい時,効率が最大となることを覚えていれば問題ありません。
5.電圧変動率の近似式
変圧器の無負荷時の二次側端子電圧を\( \ V_{\mathrm {20}} \ \),定格二次電圧\( \ V_{\mathrm {2n}} \ \)をとすると,電圧変動率\( \ \varepsilon \ \)は,
\[
\varepsilon =\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ [%]
\]
で定義され,ベクトル図を描くと図3の通りとなるので,位相差\( \ \delta \ \)が十分に小さいとすると,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ]
&≒&\frac {r_{21}I_{\mathrm {2n}}\cos \theta +x_{21}I_{\mathrm {2n}}\sin \theta }{V_{\mathrm {2n}}}\times 100 \\[ 5pt ]
&=&\frac {r_{21}I_{\mathrm {2n}}}{V_{\mathrm {2n}}}\cos \theta \times 100 +\frac {x_{21}I_{\mathrm {2n}}}{V_{\mathrm {2n}}}\sin \theta \times 100 \\[ 5pt ]
&=&p\cos \theta +q\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。このときの\( \ p \ \)を百分率抵抗降下,\( \ q \ \)を百分率リアクタンス降下といいます。
なお,本問で与えられている式はもう少し厳密な電圧変動率の式となります。もう少し詳しく知りたい方は電気の神髄HPを参照して下さい。

【関連する「電気の神髄」記事】
【解答】
(1)一次側から見た簡易等価回路の回路定数をそれぞれ求める
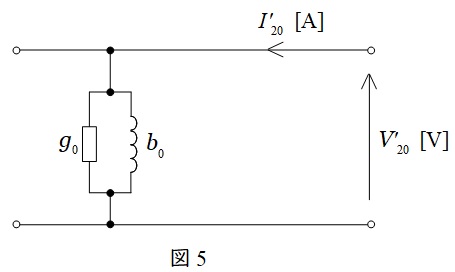
題意より,無負荷試験時の巻線抵抗\( \ R \ \)と漏れリアクタンス\( \ X \ \)による電圧降下は無視できるので,等価回路は図5のようになる。ただし,\( \ V_{\mathrm {20}}^{\prime } \ \)は無負荷試験時の電圧\( \ V_{\mathrm {20}} \ \)の一次側換算,\( \ I_{\mathrm {20}}^{\prime } \ \)は無負荷試験時の電流\( \ I_{\mathrm {20}} \ \)の一次側換算である。
ここで,\( \ V_{\mathrm {20}}^{\prime } \ \)及び\( \ I_{\mathrm {20}}^{\prime } \ \)は,定格一次電圧\( \ V_{\mathrm {1n}}=66 \ \mathrm {[kV]} \ \),定格二次電圧\( \ V_{\mathrm {2n}}=11 \ \mathrm {[kV]} \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {20}}^{\prime } &=& \frac {V_{\mathrm {1n}}}{V_{\mathrm {2n}}}\cdot V_{\mathrm {20}} \\[ 5pt ]
&=& \frac {66\times 10^{3}}{11\times 10^{3}}\times 11000 \\[ 5pt ]
&=& 66000 \ \mathrm {[V]} \\[ 5pt ]
I_{\mathrm {20}}^{\prime } &=& \frac {V_{\mathrm {2n}}}{V_{\mathrm {1n}}}\cdot I_{\mathrm {20}} \\[ 5pt ]
&=& \frac {11\times 10^{3}}{66\times 10^{3}}\times 44 \\[ 5pt ]
&≒& 7.3333 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,オームの法則より励磁回路のアドミタンス\( \ Y_{\mathrm {0}}=\sqrt {g_{\mathrm {0}}^{2}+b_{\mathrm {0}}^{2}} \ \)は,
\[
\begin{eqnarray}
Y_{\mathrm {0}} &=& \frac {I_{\mathrm {20}}^{\prime }}{V_{\mathrm {20}}^{\prime }} \\[ 5pt ]
&=& \frac {7.3333}{66000} \\[ 5pt ]
&≒& 1.1111\times 10^{-4} \ \mathrm {[S]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,電力\( \ P_{\mathrm {20}}=55 \ \mathrm {[kW]} \ \)であるから,
\[
\begin{eqnarray}
P_{\mathrm {20}} &=& g_{0}{V_{\mathrm {20}}^{\prime }}^{2}\\[ 5pt ]
g_{0}&=& \frac {P_{\mathrm {20}}}{{V_{\mathrm {20}}^{\prime }}^{2}} \\[ 5pt ]
&=& \frac {55\times 10^{3}}{66000^{2}} \\[ 5pt ]
&≒& 1.2626\times 10^{-5} → 1.26\times 10^{-5} \ \mathrm {[S]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,\( \ Y_{\mathrm {0}}=\sqrt {g_{\mathrm {0}}^{2}+b_{\mathrm {0}}^{2}} \ \)より,
\[
\begin{eqnarray}
b_{\mathrm {0}} &=& \sqrt {Y_{\mathrm {0}}^{2}-g_{\mathrm {0}}^{2}} \\[ 5pt ]
&=& \sqrt {\left( 1.1111\times 10^{-4}\right) ^{2}-\left( 1.2626\times 10^{-5}\right) ^{2}} \\[ 5pt ]
&≒& 1.1039\times 10^{-4} → 1.10\times 10^{-4} \ \mathrm {[S]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
次に,短絡試験時は鉄損を無視できるので,等価回路は図6のようになる。ただし,\( \ V_{\mathrm {2s}}^{\prime } \ \)は短絡試験時の電圧\( \ V_{\mathrm {2s}} \ \)の一次側換算,\( \ I_{\mathrm {2s}}^{\prime } \ \)は短絡試験時の電流\( \ I_{\mathrm {2s}} \ \)の一次側換算である。
\( \ V_{\mathrm {2s}}^{\prime } \ \)及び\( \ I_{\mathrm {2s}}^{\prime } \ \)は,定格一次電圧\( \ V_{\mathrm {1n}}=66 \ \mathrm {[kV]} \ \),定格二次電圧\( \ V_{\mathrm {2n}}=11 \ \mathrm {[kV]} \ \)であるから,
\[
\begin{eqnarray}
V_{\mathrm {2s}}^{\prime } &=& \frac {V_{\mathrm {1n}}}{V_{\mathrm {2n}}}\cdot V_{\mathrm {2s}} \\[ 5pt ]
&=& \frac {66\times 10^{3}}{11\times 10^{3}}\times 660 \\[ 5pt ]
&=& 3960 \ \mathrm {[V]} \\[ 5pt ]
I_{\mathrm {2s}}^{\prime } &=& \frac {V_{\mathrm {2n}}}{V_{\mathrm {1n}}}\cdot I_{\mathrm {2s}} \\[ 5pt ]
&=& \frac {11\times 10^{3}}{66\times 10^{3}}\times 1364 \\[ 5pt ]
&≒& 227.33 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ R \ \)と\( \ X \ \)の合成インピーダンス\( \ Z=\sqrt {R^{2}+X^{2}} \ \)は,
\[
\begin{eqnarray}
Z &=& \frac {V_{\mathrm {2s}}^{\prime }}{I_{\mathrm {2s}}^{\prime }} \\[ 5pt ]
&=& \frac {3960}{227.33} \\[ 5pt ]
&≒& 17.419 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,電力\( \ P_{\mathrm {2s}}=110 \mathrm {[kW]} \ \)であるから,
\[
\begin{eqnarray}
P_{\mathrm {2s}} &=& R{I_{\mathrm {2s}}^{\prime }}^{2}\\[ 5pt ]
R&=& \frac {P_{\mathrm {2s}}}{{I_{\mathrm {2s}}^{\prime }}^{2}} \\[ 5pt ]
&=& \frac {110\times 10^{3}}{227.33^{2}} \\[ 5pt ]
&≒& 2.1285 → 2.13 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,\( \ Z=\sqrt {R^{2}+X^{2}} \ \)より,
\[
\begin{eqnarray}
X &=& \sqrt {Z^{2}-R^{2}} \\[ 5pt ]
&=& \sqrt {17.419 ^{2}-2.1285 ^{2}} \\[ 5pt ]
&≒& 17.288 → 17.3 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。

(2)百分率抵抗降下\( \ p \ \mathrm {[%]} \ \),百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)及び百分率インピーダンス\( \ z \ \mathrm {[%]} \ \)を求める
定格容量\( \ P_{\mathrm {n}}=15 \ 000 \ \mathrm {[kV\cdot A]} \ \)であり,定格一次電圧\( \ V_{\mathrm {1n}}=66 \ \mathrm {[kV]} \ \)であるから,定格一次電流\( \ I_{\mathrm {1n}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {1n}} &=&\frac {P_{\mathrm {n}}}{V_{\mathrm {1n}}} \\[ 5pt ]
&=&\frac {15000\times 10^{3}}{66\times 10^{3}} \\[ 5pt ]
&≒& 227.27 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,百分率抵抗降下\( \ p \ \mathrm {[%]} \ \),百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)は,ワンポイント解説「5.電圧変動率の近似式」の通り,
\[
\begin{eqnarray}
p &=&\frac {RI_{\mathrm {1n}}}{V_{\mathrm {1n}}}\times 100 \\[ 5pt ]
&=&\frac {2.1285\times 227.27}{66\times 10^{3}}\times 100 \\[ 5pt ]
&≒& 0.73295 → 0.733 \ \mathrm {[%]} \\[ 5pt ]
q &=&\frac {XI_{\mathrm {1n}}}{V_{\mathrm {1n}}}\times 100 \\[ 5pt ]
&=&\frac {17.288\times 227.27}{66\times 10^{3}}\times 100 \\[ 5pt ]
&≒& 5.9531 → 5.95 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,\( \ z=\sqrt {p^{2}+q^{2}} \ \)の関係があるから,
\[
\begin{eqnarray}
z &=&\sqrt {p^{2}+q^{2}} \\[ 5pt ]
&=&\sqrt {0.73295^{2}+5.9531^{2}} \\[ 5pt ]
&≒& 5.9981 → 6.00 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)遅れ力率\( \ 80 \ \mathrm {%} \ \)で定格容量の負荷における電圧の変動率\( \ \varepsilon \ \mathrm {[%]} \ \)
力率\( \ \cos \theta =0.8 \ \)であるから,
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&\sqrt {1-0.8 ^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
となるので,問で与えられている電圧変動率の式に各値を代入すると,
\[
\begin{eqnarray}
\varepsilon &=&p\cos \theta +q\sin \theta +\frac {1}{200}\left( q\cos \theta -p\sin \theta \right) ^{2} \\[ 5pt ]
&=&0.73295\times 0.8 +5.9531\times 0.6 +\frac {1}{200}\times \left( 5.9531\times 0.8 -0.73295\times 0.6 \right) ^{2} \\[ 5pt ]
&≒& 4.2516 → 4.25 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)力率\( \ 100 \ \mathrm {%} \ \)において効率が最大のとき,負荷電力\( \ P_{\mathrm {L}} \ \mathrm {[kW]} \ \)及び最大効率\( \ \eta _{\mathrm {m}} \ \mathrm {[%]} \ \)
定格負荷時の銅損\( \ P_{\mathrm {cn}} \ \mathrm {[kW]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {cn}} &=&RI_{\mathrm {1n}}^{2} \\[ 5pt ]
&=&2.1285\times 227.27^{2} \\[ 5pt ]
&≒& 109 \ 940 \ \mathrm {[W]} → 109.94 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「4.変圧器の効率\( \ \eta \ \)と最大効率\( \ \eta _{\mathrm {m}} \ \)」の通り,効率が最大であるときは鉄損\( \ P_{\mathrm {20}}=55 \mathrm {[kW]} \ \)と銅損が等しいときであるので,その時の負荷率\( \ \alpha \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {20}} &=&\alpha ^{2}P_{\mathrm {cn}} \\[ 5pt ]
\alpha &=&\sqrt {\frac {P_{\mathrm {20}}}{P_{\mathrm {cn}}}} \\[ 5pt ]
&=&\sqrt {\frac {55}{109.94}} \\[ 5pt ]
&≒& 0.70730 \\[ 5pt ]
\end{eqnarray}
\]
となるので,そのときの負荷電力\( \ P_{\mathrm {L}} \ \mathrm {[kW]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {L}} &=&\alpha P_{\mathrm {n}} \\[ 5pt ]
&=&0.70730\times 15 \ 000 \\[ 5pt ]
&≒& 10 \ 610 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,そのときの最大効率\( \ \eta _{\mathrm {m}} \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
\eta _{\mathrm {m}} &=&\frac {P_{\mathrm {L}}}{\displaystyle P_{\mathrm {L}}+2P_{\mathrm {20}}}\times 100 \\[ 5pt ]
&=&\frac {10610 }{10610+2\times 55}\times 100 \\[ 5pt ]
&≒&98.974 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん