【問題】
【難易度】★★★☆☆(普通)
直軸同期リアクタンスが\( \ X_{\mathrm {d}} \ \left( \ =2.0 \ \mathrm {p.u.} \ \right) \ \),横軸同期リアクタンスが\( \ X_{\mathrm {q}} \ \left( \ =0.9 \ \mathrm {p.u.} \ \right) \ \)である三相突極形同期発電機を,端子電圧\( \ V \ \mathrm {[p.u.]} \ \),電機子電流\( \ I \ \mathrm {[p.u.]} \ \),及び力率\( \ \cos \varphi \ \)で運転した場合に,次の問に答えよ。なお,単位法は自己定格容量及び自己定格電圧を基準とし,電機子抵抗は無視する。
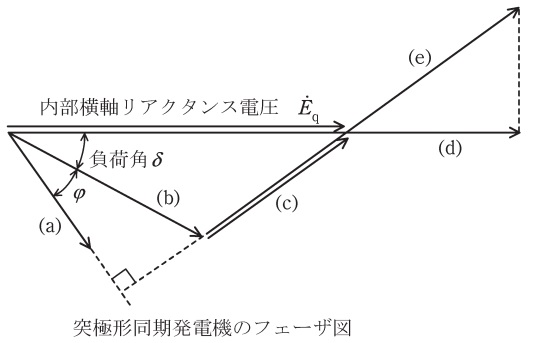
(1) 図は突極形同期発電機のフェーザ図である。図において下記の諸量に対応するフェーザを図中の記号で答えよ。なお,電気諸量の単位は\( \ \mathrm {p.u.} \ \)とする。
① 発電機端子電圧 \( \ \dot V \ \)
② 無負荷誘導起電力 \( \ \dot E \ \)
③ 電機子電流 \( \ \dot I \ \)
④ 直軸同期リアクタンス電圧降下 \( \ \mathrm {j} X_{\mathrm {d}}\dot I \ \)
⑤ 横軸同期リアクタンス電圧降下 \( \ \mathrm {j} X_{\mathrm {q}}\dot I \ \)
(解答例 ① (a),② (b),\(\cdots \))
(2) この発電機の定格運転\( \ \left( \ V=1.0 \ \mathrm {p.u.} , I=1.0 \ \mathrm {p.u.} , \cos \varphi =0.8 \ \right) \ \)における\( \ E_{\mathrm {q}} \ \mathrm {[p.u.]} \ \),\( \ \sin \left( \varphi +\delta \right) \ \),及び\( \ E \ \mathrm {[p.u.]} \ \)の値を求めよ。
(3) この発電機の運転において,\( \ E \ \),\( \ V \ \)を一定として機械入力を徐々に増加させてゆく場合の発電機の定態安定限界出力における負荷角を\( \ \delta _{\mathrm {m}} \ \)とする。このときの\( \ \cos \delta _{\mathrm {m}} \ \)を\( \ V \ \),\( \ X_{\mathrm {d}} \ \),\( \ X_{\mathrm {q}} \ \),及び\( \ E \ \)で表せ。
なお,突極形同期発電機の出力\( \ P \ \mathrm {[p.u.]} \ \)は一般に下記の①式で表すことができ,\( \ \cos \delta _{\mathrm {m}} \ \)の導出にはこの式を利用してよい。
\[
\begin{eqnarray}
P \ \mathrm {[p.u.]}&=&\frac {VE}{X_{\mathrm {d}}}\sin \delta +\frac {1}{2}\left( \frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}\right) V^{2}\sin 2\delta ・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
(4) 小問(2)の定格運転状態から,小問(3)と同じ条件で機械入力を増加させる場合の\( \ \cos \delta _{\mathrm {m}} \ \)の値を求めよ。
【ワンポイント解説】
突極形同期発電機に関する問題です。
一般に電験\( \ 2 \ \)種までは円筒形の同期発電機について出題されており,その場合は同期リアクタンスのみを検討すれば良いのですが,\( \ 1 \ \)種になると突極形同期発電機の内容が出題され,その場合には直軸同期リアクタンスと横軸同期リアクタンスが等しくならないので,本問のようにそれぞれ別に検討する必要があります。
少し計算量は多めですが,難易度はそれほど高くないので,本問で理解するようにしましょう。
1.突極形同期発電機の構造及びベクトル図
突極形同期発電機の構造は図1のようになり,回転子の磁極と同じ向きの軸を直軸(\( \ \mathrm {d} \ \)軸),磁極と直角の向きの軸を横軸(\( \ \mathrm {q} \ \)軸)といいます。
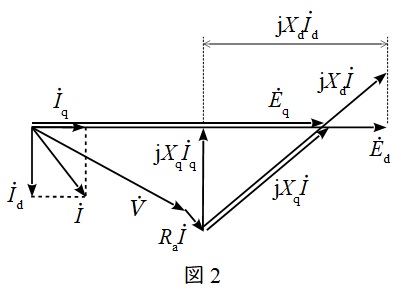
円筒機は直軸同期リアクタンス\( \ X_{\mathrm {d}} \ \)と横軸同期リアクタンス\( \ X_{\mathrm {q}} \ \)がほぼ等しいので,基本的な同期発電機の等価回路やベクトル図が適用できますが,突極機の場合はその構造上\( \ X_{\mathrm {d}}>X_{\mathrm {q}} \ \)となるので,ベクトル図としては図2のようになります。
(\( \ X_{\mathrm {d}}>X_{\mathrm {q}} \ \)となる理由はかなり専門性が強い内容なので,ご興味のある方は専門書をご覧下さい。\( \ \mathrm {d} \ \)軸方向が鉄心がある分インダクタンスが大きくなり,それに比例するリアクタンスが大きくなるぐらいのイメージで十分です。)
図2において,\( \ {\dot E}_{\mathrm {d}} \ \):無負荷誘導起電力,\( \ {\dot E}_{\mathrm {q}} \ \):内部横軸リアクタンス電圧,\( \ \dot I \ \):電機子電流,\( \ {\dot I}_{\mathrm {d}} \ \):電機子電流の直軸分,\( \ {\dot I}_{\mathrm {q}} \ \):電機子電流の横軸分,\( \ R_{\mathrm {a}} \ \):電機子抵抗(無視することも多い),となります。

【解答】
(1)フェーザ図において各諸量に対応するフェーザを図中の記号で答える
ワンポイント解説「1.突極形同期発電機の構造及びベクトル図」の通り,
① 発電機端子電圧 \( \ \dot V \ \) → (b)
② 無負荷誘導起電力 \( \ \dot E \ \) → (d)
③ 電機子電流 \( \ \dot I \ \) → (a)
④ 直軸同期リアクタンス電圧降下 \( \ \mathrm {j} X_{\mathrm {d}}\dot I \ \) → (e)
⑤ 横軸同期リアクタンス電圧降下 \( \ \mathrm {j} X_{\mathrm {q}}\dot I \ \) → (c)
と求められる。
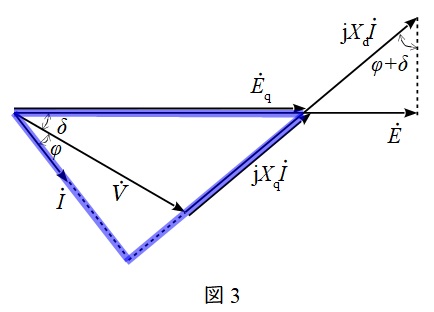
(2)定格運転における\( \ E_{\mathrm {q}} \ \mathrm {[p.u.]} \ \),\( \ \sin \left( \varphi +\delta \right) \ \),及び\( \ E \ \mathrm {[p.u.]} \ \)の値
図3に示す三角形に三平方の定理を適用すると,
\[
\begin{eqnarray}
E_{\mathrm {q}}&=&\sqrt {\left( V\cos \varphi \right) ^{2}+\left( V\sin \varphi +X_{\mathrm {q}}I\right) ^{2}} \\[ 5pt ]
&=&\sqrt {\left( V\cos \varphi \right) ^{2}+\left( V\sqrt {1-\cos ^{2}\varphi } +X_{\mathrm {q}}I\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,各値を代入すると,
\[
\begin{eqnarray}
E_{\mathrm {q}}&=&\sqrt {\left( 1.0\times 0.8 \right) ^{2}+\left( 1.0 \times \sqrt {1-0.8^{2}} +0.9\times 1.0\right) ^{2}} \\[ 5pt ]
&=&\sqrt {0.8^{2}+1.5^{2}} \\[ 5pt ]
&=&1.7 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。次に\( \ \sin \left( \varphi +\delta \right) \ \)は,
\[
\begin{eqnarray}
\sin \left( \varphi +\delta \right) &=&\frac {V\sin \varphi +X_{\mathrm {q}}I}{E_{\mathrm {q}}} \\[ 5pt ]
&=&\frac {1.5 }{1.7} \\[ 5pt ]
&≒&0.88235 → 0.882 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。最後に\( \ E \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
E &=&E_{\mathrm {q}}+\left( X_{\mathrm {d}}I-X_{\mathrm {q}}I\right) \sin \left( \varphi +\delta \right) \\[ 5pt ]
&=&1.7+\left( 2.0\times 1-0.9\times 1\right) \times 0.88235 \\[ 5pt ]
&≒&2.6706 → 2.67 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)定態安定限界出力における負荷角を\( \ \delta _{\mathrm {m}} \ \)としたときの\( \ \cos \delta _{\mathrm {m}} \ \)
①式の通り,
\[
\begin{eqnarray}
P \ \mathrm {[p.u.]}&=&\frac {VE}{X_{\mathrm {d}}}\sin \delta +\frac {1}{2}\left( \frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}\right) V^{2}\sin 2\delta \\[ 5pt ]
\end{eqnarray}
\]
であるから,両辺\( \ \delta \ \)で微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}\delta }&=&\frac {VE}{X_{\mathrm {d}}}\cos \delta +\frac {1}{2}\left( \frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}\right) V^{2}\times 2\cos 2\delta \\[ 5pt ]
&=&\frac {VE}{X_{\mathrm {d}}}\cos \delta +\left( \frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}\right) V^{2}\cos 2\delta \\[ 5pt ]
\end{eqnarray}
\]
となる。発電機の定態安定限界出力すなわち出力が最大となるとき,\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta }=0 \ \)であるから,
\[
\begin{eqnarray}
\frac {VE}{X_{\mathrm {d}}}\cos \delta _{\mathrm {m}}+\left( \frac {1}{X_{\mathrm {q}}}-\frac {1}{X_{\mathrm {d}}}\right) V^{2}\cos 2\delta _{\mathrm {m}}&=&0 \\[ 5pt ]
\frac {VE}{X_{\mathrm {d}}}\cos \delta _{\mathrm {m}}+\left( \frac {X_{\mathrm {d}}-X_{\mathrm {q}}}{X_{\mathrm {d}}X_{\mathrm {q}}}\right) V^{2}\left( 2\cos ^{2}\delta _{\mathrm {m}}-1\right) &=&0 \\[ 5pt ]
X_{\mathrm {q}}VE\cos \delta _{\mathrm {m}}+\left( X_{\mathrm {d}}-X_{\mathrm {q}}\right) V^{2}\left( 2\cos ^{2}\delta _{\mathrm {m}}-1\right) &=&0 \\[ 5pt ]
X_{\mathrm {q}}E\cos \delta _{\mathrm {m}}+\left( X_{\mathrm {d}}-X_{\mathrm {q}}\right) V\left( 2\cos ^{2}\delta _{\mathrm {m}}-1\right) &=&0 \\[ 5pt ]
2\left( X_{\mathrm {d}}-X_{\mathrm {q}}\right) V\cos ^{2}\delta _{\mathrm {m}}+X_{\mathrm {q}}E\cos \delta _{\mathrm {m}}-\left( X_{\mathrm {d}}-X_{\mathrm {q}}\right) V &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,解の公式を適用すると,
\[
\begin{eqnarray}
\cos \delta _{\mathrm {m}}&=&\frac {-X_{\mathrm {q}}E±\sqrt {\left( X_{\mathrm {q}}E\right) ^{2}+8\left( X_{\mathrm {d}}-X_{\mathrm {q}}\right) ^{2}V^{2}}}{4\left( X_{\mathrm {d}}-X_{\mathrm {q}}\right) V} \\[ 5pt ]
\end{eqnarray}
\]
と計算され,\( \ \cos \delta _{\mathrm {m}}>0 \ \)であるから,
\[
\begin{eqnarray}
\cos \delta _{\mathrm {m}}&=&\frac {-X_{\mathrm {q}}E+\sqrt {\left( X_{\mathrm {q}}E\right) ^{2}+8\left( X_{\mathrm {d}}-X_{\mathrm {q}}\right) ^{2}V^{2}}}{4\left( X_{\mathrm {d}}-X_{\mathrm {q}}\right) V} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)小問(2)の定格運転状態から,小問(3)と同じ条件で機械入力を増加させる場合の\( \ \cos \delta _{\mathrm {m}} \ \)の値
(3)解答式に各値を代入すると,
\[
\begin{eqnarray}
\cos \delta _{\mathrm {m}}&=&\frac {-0.9 \times 2.6706+\sqrt {\left( 0.9 \times 2.6706\right) ^{2}+8\times \left( 2.0-0.9\right) ^{2}\times 1.0^{2}}}{4\times \left( 2.0-0.9\right) \times 1.0} \\[ 5pt ]
&=&\frac {-2.40354+\sqrt {2.40354 ^{2}+9.68}}{4.4} \\[ 5pt ]
&≒&0.34727 → 0.347 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん