【問題】
【難易度】★★☆☆☆(やや易しい)
定格電圧(相電圧)が\( \ V_{\mathrm {n}} \ \mathrm {[p.u.]} \ \),定格電流が\( \ I_{\mathrm {n}} \ \mathrm {[p.u.]} \ \),定格力率が\( \ \cos \theta _{\mathrm {n}} \ \)\( \left( 80 \ \mathrm {%} \right. \ \)遅れ\(\left. \right) \),及び同期リアクタンスが\( \ X_{\mathrm {s}} \ \)である三相円筒形同期発電機に関して,次の問に答えよ。なお,単位法は自己定格容量及び自己定格電圧を基準とし,電機子抵抗や磁気飽和は無視する。
(1) この発電機のフェーザ図を端子電圧(相電圧)を基準にして描き,図中に\( \ {\dot V}_{\mathrm {n}} \ \),\( \ {\dot I}_{\mathrm {n}} \ \),\( \ \mathrm {j}X_{\mathrm {s}}{\dot I}_{\mathrm {n}} \ \),\( \ \theta _{\mathrm {n}} \ \),及び定格時の無負荷誘導起電力\( \ {\dot E}_{\mathrm {n}} \ \),を示せ。
(2) 同期機の電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)は,定格運転状態から回転速度と界磁電流を一定に保って無負荷にしたときの端子電圧の変化率を表したものである。\( \ \varepsilon \ \mathrm {[%]} \ \)を表す式を\( \ E_{\mathrm {n}} \ \)と\( \ V_{\mathrm {n}} \ \)を用いて示せ。
(3) フェーザ図から,\( \ E_{\mathrm {n}} \ \)を\( \ V_{\mathrm {n}} \ \),\( \ \theta _{\mathrm {n}} \ \),及び\( \ X_{\mathrm {s}}I_{\mathrm {n}} \ \)で表す式を導出し,さらに\( \ \varepsilon \ \)を\( \ V_{\mathrm {n}} \ \),\( \ \theta _{\mathrm {n}} \ \),及び\( \ X_{\mathrm {s}}I_{\mathrm {n}} \ \)を用いて表す式を示せ。
(4)
a.この発電機の同期リアクタンス\( \ X_{\mathrm {s}} \ \)を\( \ 1.25 \ \mathrm {p.u.} \ \)として,電圧変動率\( \ \varepsilon \ \)の値を求めよ。
b.次に,この発電機を定格電圧,定格電流,及び力率\( \ 100 \ \mathrm {%} \ \)で運転する場合に,そのときの端子電圧の変動率\( \ \varepsilon ^{\prime } \ \mathrm {[%]} \ \)の値を求めよ。ただし,\( \ \varepsilon ^{\prime } \ \)は,任意の運転状態から無負荷にした場合の端子電圧の変動率とする。
c.上記の問題の結果のように同じ発電機でも力率が\( \ 80 \ \mathrm {%} \ \)と\( \ 100 \ \mathrm {%} \ \)の場合で電圧の変動率が異なる理由を,\( \ 150 \ \)字を上限としてできるだけ簡単に述べよ。
(5) 同期発電機の電圧変動率\( \ \varepsilon \ \)は,短絡比が大きい発電機の方がより小さい値になる。発電機の定格力率が\( \ 80 \ \mathrm {%} \ \)遅れの場合,その電圧変動率\( \ \varepsilon \ \)が \( \ 50 \ \mathrm {%} \ \)になるような発電機の同期リアクタンスを求めよ。
【ワンポイント解説】
三相同期発電機のベクトル図を使った計算問題です。
内容はそれほど難しくありませんが,問題数と計算量が多い問題であるため,\( \ 30 \ \)分で完答するのは少し厳しいかもしれません。
計算力に自信のある方は最優先に取り組んでも良い問題とも言えるでしょう。
1.同期発電機の等価回路とベクトル図
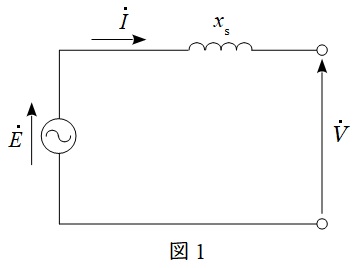
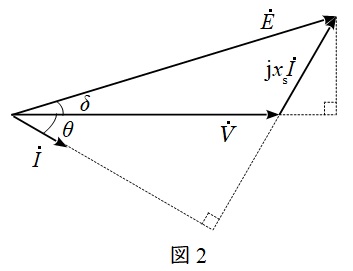
三相同期発電機の誘導起電力(相電圧)を\( \ \dot E \ \mathrm {[V]} \ \),端子電圧(相電圧)を\( \ \dot V \ \mathrm {[V]} \ \),同期リアクタンスを\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \),電機子電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると,一相分等価回路は図1,ベクトル図は図2のように描くことができます。
一般に同期機においては電機子巻線抵抗等の抵抗分は十分に小さいと考え無視します。
2.同期機の電圧変動率\( \ \varepsilon \ \)
同期機の電圧変動率\( \ \varepsilon \ \)は,無負荷としたときの端子電圧(内部誘導起電力)を\( \ E \ \mathrm {[V]} \ \),定格の端子電圧を\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)としたとき,
\[
\begin{eqnarray}
\varepsilon &=&\frac {E-V_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
で定義されます。
【解答】
(1)フェーザ図を端子電圧(相電圧)を基準にして描く
ワンポイント解説「1.同期発電機の等価回路とベクトル図」の通りフェーザ図を描き,\( \ {\dot V}_{\mathrm {n}} \ \),\( \ {\dot I}_{\mathrm {n}} \ \),\( \ \mathrm {j}X_{\mathrm {s}}{\dot I}_{\mathrm {n}} \ \),\( \ \theta _{\mathrm {n}} \ \),及び\( \ {\dot E}_{\mathrm {n}} \ \)を記載すると,図3のようになる。
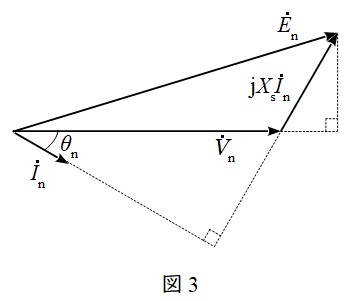
(2)電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)を表す式
ワンポイント解説「2.同期機の電圧変動率\( \ \varepsilon \ \)」の通り,電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&\frac {E_{\mathrm {n}}-V_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ E_{\mathrm {n}} \ \)を\( \ V_{\mathrm {n}} \ \),\( \ \theta _{\mathrm {n}} \ \),及び\( \ X_{\mathrm {s}}I_{\mathrm {n}} \ \)で表す式,\( \ \varepsilon \ \)を\( \ V_{\mathrm {n}} \ \),\( \ \theta _{\mathrm {n}} \ \),及び\( \ X_{\mathrm {s}}I_{\mathrm {n}} \ \)で表す式
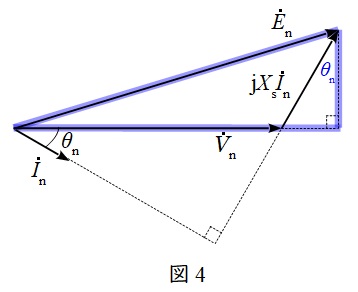
図4に示すフェーザ図の直角三角形に三平方の定理を適用すると,
\[
\begin{eqnarray}
E_{\mathrm {n}}^{2} &=&\left( V_{\mathrm {n}}+X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta _{\mathrm {n}}\right) ^{2}+\left( X_{\mathrm {s}}I_{\mathrm {n}}\cos \theta _{\mathrm {n}}\right) ^{2} \\[ 5pt ]
E_{\mathrm {n}} &=&\sqrt {\left( V_{\mathrm {n}}+X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta _{\mathrm {n}}\right) ^{2}+\left( X_{\mathrm {s}}I_{\mathrm {n}}\cos \theta _{\mathrm {n}}\right) ^{2}} \\[ 5pt ]
&=&\sqrt { V_{\mathrm {n}}^{2}+2V_{\mathrm {n}}X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta _{\mathrm {n}}+X_{\mathrm {s}}^{2}I_{\mathrm {n}}^{2}\sin ^{2}\theta _{\mathrm {n}}+ X_{\mathrm {s}}^{2}I_{\mathrm {n}}^{2}\cos ^{2}\theta _{\mathrm {n}}} \\[ 5pt ]
&=&\sqrt { V_{\mathrm {n}}^{2}+2V_{\mathrm {n}}X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta _{\mathrm {n}}+X_{\mathrm {s}}^{2}I_{\mathrm {n}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。これを(2)解答式に代入すれば,
\[
\begin{eqnarray}
\varepsilon &=&\frac {E_{\mathrm {n}}-V_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {\sqrt { V_{\mathrm {n}}^{2}+2V_{\mathrm {n}}X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta _{\mathrm {n}}+X_{\mathrm {s}}^{2}I_{\mathrm {n}}^{2}}-V_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}\sqrt { 1+\displaystyle \frac {2X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta _{\mathrm {n}}}{V_{\mathrm {n}}}+\frac {X_{\mathrm {s}}^{2}I_{\mathrm {n}}^{2}}{V_{\mathrm {n}}^{2}}}-V_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\left( \sqrt { 1+\displaystyle \frac {2X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta _{\mathrm {n}}}{V_{\mathrm {n}}}+\frac {X_{\mathrm {s}}^{2}I_{\mathrm {n}}^{2}}{V_{\mathrm {n}}^{2}}}-1\right) \times 100 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)a.\( \ X_{\mathrm {s}} \ \)を\( \ 1.25 \ \mathrm {p.u.} \ \)としたときの電圧変動率\( \ \varepsilon \ \)の値
題意より,\( \ \cos \theta _{\mathrm {n}}=0.8 \ \)であるから,
\[
\begin{eqnarray}
\sin \theta _{\mathrm {n}} &=&\sqrt {1-\cos ^{2}\theta _{\mathrm {n}}} \\[ 5pt ]
&=&\sqrt {1-0.8 ^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ V_{\mathrm {n}}=1 \ \mathrm {[p.u.]} \ \),\( \ I_{\mathrm {n}}=1 \ \mathrm {[p.u.]} \ \),\( \ X_{\mathrm {s}}=1.25 \ \mathrm {[p.u.]} \ \),\( \ \sin \theta _{\mathrm {n}}=0.6 \ \)を(3)解答式に代入すると,
\[
\begin{eqnarray}
\varepsilon &=&\left( \sqrt { 1+\displaystyle \frac {2X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta _{\mathrm {n}}}{V_{\mathrm {n}}}+\frac {X_{\mathrm {s}}^{2}I_{\mathrm {n}}^{2}}{V_{\mathrm {n}}^{2}}}-1\right) \times 100 \\[ 5pt ]
&=&\left( \sqrt { 1+\displaystyle \frac {2\times 1.25\times 1\times 0.6}{1}+\frac {1.25^{2}\times 1^{2}}{1^{2}}}-1\right) \times 100 \\[ 5pt ]
&=&\left( \sqrt { 1+1.5+1.5625}-1\right) \times 100 \\[ 5pt ]
&≒&101.56 → 102 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)b.力率\( \ 100 \ \mathrm {%} \ \)で運転する場合の端子電圧の変動率\( \ \varepsilon ^{\prime } \ \mathrm {[%]} \ \)の値
\( \ \sin \theta _{\mathrm {n}} =0 \ \)であるから,\( \ V_{\mathrm {n}}=1 \ \mathrm {[p.u.]} \ \),\( \ I_{\mathrm {n}}=1 \ \mathrm {[p.u.]} \ \),\( \ X_{\mathrm {s}}=1.25 \ \mathrm {[p.u.]} \ \),\( \ \sin \theta _{\mathrm {n}}=0 \ \)を(3)解答式に代入すると,
\[
\begin{eqnarray}
\varepsilon &=&\left( \sqrt { 1+\displaystyle \frac {2X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta _{\mathrm {n}}}{V_{\mathrm {n}}}+\frac {X_{\mathrm {s}}^{2}I_{\mathrm {n}}^{2}}{V_{\mathrm {n}}^{2}}}-1\right) \times 100 \\[ 5pt ]
&=&\left( \sqrt { 1+\displaystyle \frac {2\times 1.25\times 1\times 0}{1}+\frac {1.25^{2}\times 1^{2}}{1^{2}}}-1\right) \times 100 \\[ 5pt ]
&=&\left( \sqrt { 1+0+1.5625}-1\right) \times 100 \\[ 5pt ]
&≒&60.078 → 60.1 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)c.同じ発電機でも力率が\( \ 80 \ \mathrm {%} \ \)と\( \ 100 \ \mathrm {%} \ \)の場合で電圧の変動率が異なる理由
(ポイント)
・電機子反作用が最大のポイントです。遅れ力率の場合に電機子反作用がどのように内部誘導起電力に影響するかを記載すれば最適解となります。
(試験センター解答)
力率が遅れ\( \ 80 \ \mathrm {%} \ \)の場合では電機子反作用中に減磁作用成分が含まれるが,力率が\( \ 100 \ \mathrm {%} \ \)では電機子反作用は交差磁化作用となる。このため端子電圧を\( \ 1 \ \mathrm {p.u.} \ \)にするための界磁電流すなわち無負荷誘導起電力は,力率\( \ 100 \ \mathrm {%} \ \)より遅れ力率\( \ 80 \ \mathrm {%} \ \)の場合の方が大きくなり,電圧変動率\( \ \varepsilon \ \)は遅れ力率\( \ 80 \ \mathrm {%} \ \)の場合の方が大きくなる。
(5)力率が\( \ 80 \ \mathrm {%} \ \)遅れの場合,その電圧変動率\( \ \varepsilon \ \)が \( \ 50 \ \mathrm {%} \ \)になるような発電機の同期リアクタンス
(3)解答式に\( \ \varepsilon =50 \ \mathrm {[%]} \ \),\( \ V_{\mathrm {n}}=1 \ \mathrm {[p.u.]} \ \),\( \ I_{\mathrm {n}}=1 \ \mathrm {[p.u.]} \ \),\( \ \sin \theta _{\mathrm {n}}=0.6 \ \)を代入して計算すると,
\[
\begin{eqnarray}
\varepsilon &=&\left( \sqrt { 1+\displaystyle \frac {2X_{\mathrm {s}}I_{\mathrm {n}}\sin \theta _{\mathrm {n}}}{V_{\mathrm {n}}}+\frac {X_{\mathrm {s}}^{2}I_{\mathrm {n}}^{2}}{V_{\mathrm {n}}^{2}}}-1\right) \times 100 \\[ 5pt ]
50 &=&\left( \sqrt { 1+\displaystyle \frac {2X_{\mathrm {s}}\times 1\times 0.6}{1}+\frac {X_{\mathrm {s}}^{2}\times 1^{2}}{1^{2}}}-1\right) \times 100 \\[ 5pt ]
0.5 &=& \sqrt { 1+1.2X_{\mathrm {s}}+X_{\mathrm {s}}^{2}}-1 \\[ 5pt ]
\sqrt { 1+1.2X_{\mathrm {s}}+X_{\mathrm {s}}^{2}} &=& 1.5 \\[ 5pt ]
1+1.2X_{\mathrm {s}}+X_{\mathrm {s}}^{2} &=& 2.25\\[ 5pt ]
X_{\mathrm {s}}^{2}+1.2X_{\mathrm {s}}-1.25 &=& 0 \\[ 5pt ]
X_{\mathrm {s}} &=& -0.6±\sqrt {0.6^{2}+1.25} \\[ 5pt ]
&≒& 0.66886,-1.8689(不適) → 0.669 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん