【問題】
【難易度】★★☆☆☆(やや易しい)
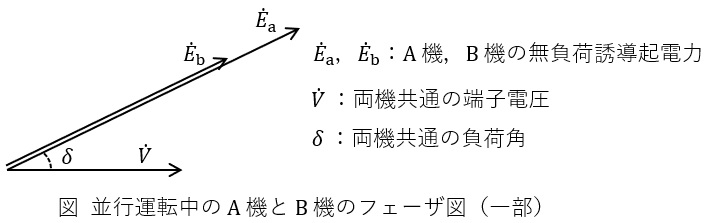
\( \ \mathrm {A} \ \)機及び\( \ \mathrm {B} \ \)機の\( \ \mathrm {2} \ \)台の三相円筒形同期発電機を共通の母線に接続して並行運転を行う。この共通母線に負荷を接続して,両機とも遅れ力率にて,また両機の負荷角が等しくなるように並行運転を行うと両機のフェーザ図の一部が図のようになった。この運転状態の発電機について,次の問に答えよ。
ここで,両機はいずれも定格皮相電力\( \ 10 \ \mathrm {MV\cdot A } \ \),定格力率\( \ 0.8 \ \)(遅れ)であり,\( \ \mathrm {A} \ \)機と\( \ \mathrm {B} \ \)機の同期リアクタンスは,\( \ X_{\mathrm {a}}=2.0 \ \mathrm {p.u.} \ \),及び\( \ X_{\mathrm {b}}=1.5 \ \mathrm {p.u.} \ \)である。なお,鉄心の磁気飽和及び発電機の損失は無視し,単位法は発電機の定格皮相電力及び定格電圧を基準,無効電力は遅れを正とする。
(1) 図を参考にして,\( \ \dot V \ \),\( \ {\dot E}_{\mathrm {a}} \ \),\( \ {\dot E}_{\mathrm {b}} \ \),\( \ \delta \ \)に加えて,\( \ \mathrm {A} \ \)機と\( \ \mathrm {B} \ \)機の電機子電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),力率角\( \ \theta _{\mathrm {a}} \ \),\( \ \theta _{\mathrm {b}} \ \),同期リアクタンス電圧降下\( \ \mathrm {j}X_{\mathrm {a}}{\dot I}_{\mathrm {a}} \ \),\( \ \mathrm {j}X_{\mathrm {b}}{\dot I}_{\mathrm {b}} \ \)を記入したフェーザ図を答案用紙に描け。なお,フェーザ図は図のように\( \ \dot V \ \)の位相を基準とし,各機単独では無く一つの図として記載せよ。
(2) この運転状態における\( \ \mathrm {A} \ \)機の諸量を有効電力\( \ P_{\mathrm {a}}=4 \ \mathrm {MW} \ \),\( \ \cos \theta _{\mathrm {a}} =0.8 \ \),\( \ V=1.0 \ \mathrm {p.u.} \ \)として,そのときの\( \ I_{\mathrm {a}} \ \mathrm {[p.u.]} \ \)を求め,さらに\( \ E_{\mathrm {a}} \ \mathrm {[p.u.]} \ \),\( \ \sin \delta \ \)の値を求めよ。
(3) また,そのときの\( \ \mathrm {B} \ \)機の有効電力を\( \ P_{\mathrm {b}}=4 \ \mathrm {MW} \ \)として,\( \ \mathrm {B} \ \)機の\( \ E_{\mathrm {b}} \ \mathrm {[p.u.]} \ \)を求め,さらに\( \ I_{\mathrm {b}} \ \mathrm {[p.u.]} \ \),\( \ \cos \theta _{\mathrm {b}} \ \),及び\( \ \mathrm {B} \ \)機が分担する無効電力\( \ Q_{\mathrm {b}} \ \mathrm {[p.u.]} \ \)の値を求めよ。
【ワンポイント解説】
同期発電機の並行運転に関する問題です。
計算量はやや多めですが,\( \ 1 \ \)種の問題としては比較的取り組みやすい問題と言えるかと思います。
本問を\( \ 30 \ \)分以内に計算間違いせずに解けると\( \ 1 \ \)種合格に大きく近づくと言えるでしょう。
1.同期発電機の等価回路とベクトル図
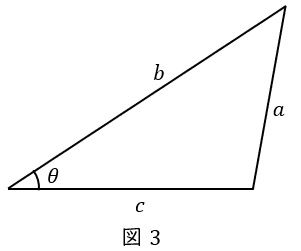
同期発電機の一相分等価回路は誘導起電力(相電圧)\( \ {\dot E}_{0} \ \mathrm {[V]} \ \),端子電圧(相電圧)\( \ \dot E \ \mathrm {[V]} \ \),同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \),電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)とすると,図1のようになります。
通常,電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)は十分に小さいと考え,無視して考えることが一般的です。
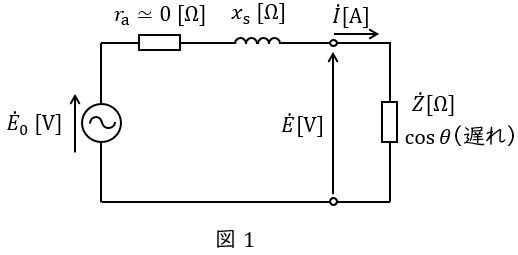
また,等価回路よりベクトル図は図2のようになります。ただし,\( \ \theta \ \)は力率角,\( \ \delta \ \)は負荷角です。
2.単位法における電力
誘導起電力(相電圧)\( \ {\dot E}_{0} \ \mathrm {[V]} \ \),端子電圧(相電圧)\( \ \dot E \ \mathrm {[V]} \ \),同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \),相電流\( \ \dot I \ \mathrm {[A]} \ \)とし,電機子巻線抵抗\( \ r_{\mathrm {a}} \ \mathrm {[\Omega ]} \ \)が無視でき,力率角\( \ \theta \ \mathrm {[rad]} \ \),負荷角\( \ \delta \ \mathrm {[rad]} \ \)としたとき,同期発電機の出力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&3EI\cos \theta \\[ 5pt ]
&=&\frac {3E_{0}E\sin \delta }{x_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
で求められますが,基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧\( \ E_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)とすると,
\[
\begin{eqnarray}
\frac {P}{P_{\mathrm {n}}} &=&\frac {3EI}{3E_{\mathrm {n}}I_{\mathrm {n}}}\cos \theta \\[ 5pt ]
\frac {P}{P_{\mathrm {n}}} &=&\frac {E}{E_{\mathrm {n}}}\frac {I}{I_{\mathrm {n}}}\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
すなわち,
\[
\begin{eqnarray}
P \ \mathrm {[p.u.]}&=&E \ \mathrm {[p.u.]}I \ \mathrm {[p.u.]}\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となり,同様に,
\[
\begin{eqnarray}
P \ \mathrm {[p.u.]} &=&\frac {E_{0} \ \mathrm {[p.u.]} \ E \ \mathrm {[p.u.]}\sin \delta }{x_{\mathrm {s}} \ \mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
となります。いずれも単位法で考える場合,係数の\( \ 3 \ \)がなくなることに注意しましょう。
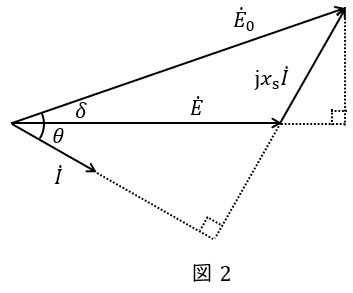
3.余弦定理
図3に示すような三角形(任意の三角形)において,
\[
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
の関係が成立し,これを余弦定理といいます。
【解答】
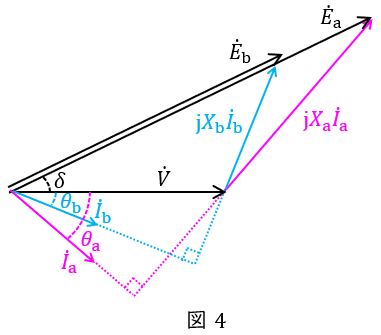
(1)電機子電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),力率角\( \ \theta _{\mathrm {a}} \ \),\( \ \theta _{\mathrm {b}} \ \),同期リアクタンス電圧降下\( \ \mathrm {j}X_{\mathrm {a}}{\dot I}_{\mathrm {a}} \ \), \( \ \mathrm {j}X_{\mathrm {b}}{\dot I}_{\mathrm {b}} \ \)を記入したフェーザ図
\( \ {\dot E}_{\mathrm {a}}=\dot V+\mathrm {j}X_{\mathrm {a}}{\dot I}_{\mathrm {a}} \ \)等に注意してフェーザ図を描くと図4のようになる。
(2)\( \ I_{\mathrm {a}} \ \mathrm {[p.u.]} \ \),\( \ E_{\mathrm {a}} \ \mathrm {[p.u.]} \ \),\( \ \sin \delta \ \)の値
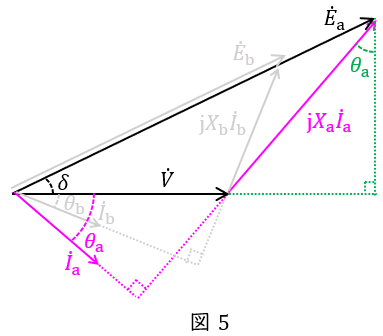
\( \ \mathrm {A} \ \)機のみに着目したフェーザ図を描くと図5の通りとなる。
単位法で表した有効電力\( \ P_{\mathrm {a}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {a}}&=&\frac {4}{10} \\[ 5pt ]
&=&0.4 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「2.単位法における電力」の通り,\( \ P_{\mathrm {a}}=VI_{\mathrm {a}}\cos \theta _{\mathrm {a}} \ \)であるから,\( \ I_{\mathrm {a}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {a}}&=&\frac {P_{\mathrm {a}}}{V\cos \theta _{\mathrm {a}} } \\[ 5pt ]
&=&\frac {0.4}{1.0\times 0.8} \\[ 5pt ]
&=&0.5 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。次に,\( \ \sin \theta _{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
\sin \theta _{\mathrm {a}}&=&\sqrt {1-\cos ^{2}\theta _{\mathrm {a}}} \\[ 5pt ]
&=&\sqrt {1-0.8^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
であり,図5に三平方の定理を適用すると\( \ E_{\mathrm {a}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {a}}&=&\sqrt {\left( V+X_{\mathrm {a}}I_{\mathrm {a}}\sin \theta _{\mathrm {a}}\right) ^{2}+\left( X_{\mathrm {a}}I_{\mathrm {a}}\cos \theta _{\mathrm {a}}\right) ^{2}} \\[ 5pt ]
&=&\sqrt {\left( 1.0+2.0\times 0.5\times 0.6\right) ^{2}+\left( 2.0\times 0.5\times 0.8\right) ^{2}} \\[ 5pt ]
&≒&1.788 \ 9 → 1.79 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。さらに図5において,\( \ E_{\mathrm {a}}\sin \delta = X_{\mathrm {a}}I_{\mathrm {a}}\cos \theta _{\mathrm {a}} \ \)の関係があるから,
\[
\begin{eqnarray}
\sin \delta &=&\frac {X_{\mathrm {a}}I_{\mathrm {a}}\cos \theta _{\mathrm {a}}}{E_{\mathrm {a}}} \\[ 5pt ]
&=&\frac {2.0\times 0.5\times 0.8}{1.788 \ 9} \\[ 5pt ]
&≒&0.447 \ 20 → 0.447 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ E_{\mathrm {b}} \ \mathrm {[p.u.]} \ \),\( \ I_{\mathrm {b}} \ \mathrm {[p.u.]} \ \),\( \ \cos \theta _{\mathrm {b}} \ \),\( \ Q_{\mathrm {b}} \ \mathrm {[p.u.]} \ \)の値
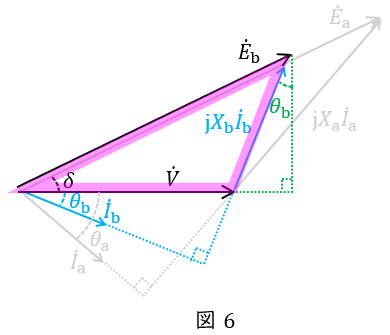
\( \ \mathrm {B} \ \)機のみに着目したフェーザ図を描くと図6の通りとなる。
単位法で表した有効電力\( \ P_{\mathrm {b}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {b}}&=&\frac {4}{10} \\[ 5pt ]
&=&0.4 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であり,本問において,\( \ \mathrm {A} \ \)機と\( \ \mathrm {B} \ \)機の負荷角は等しいので,ワンポイント解説「2.単位法における電力」の通り,\( \ \displaystyle P_{\mathrm {b}} =\frac {E_{\mathrm {b}}V\sin \delta }{X_{\mathrm {b}}} \ \)から,
\[
\begin{eqnarray}
E_{\mathrm {b}}&=&\frac {P_{\mathrm {b}}X_{\mathrm {b}}}{V\sin \delta } \\[ 5pt ]
&=&\frac {0.4\times 1.5}{1.0\times 0.44720} \\[ 5pt ]
&≒&1.341 \ 7 → 1.34 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。次に,負荷角の\( \ \cos \delta \ \)は,
\[
\begin{eqnarray}
\cos \delta &=&\sqrt {1-\sin ^{2}\delta } \\[ 5pt ]
&=&\sqrt {1-0.447 \ 20 ^{2}} \\[ 5pt ]
&≒&0.894 \ 43 \\[ 5pt ]
\end{eqnarray}
\]
なので,図6に示す三角形に余弦定理を適用し,整理して各値を代入すると,
\[
\begin{eqnarray}
\left( X_{\mathrm {b}}I_{\mathrm {b}} \right) ^{2}&=&E_{\mathrm {b}}^{2}+V^{2}-2E_{\mathrm {b}}V\cos \delta \\[ 5pt ]
X_{\mathrm {b}}I_{\mathrm {b}}&=&\sqrt {E_{\mathrm {b}}^{2}+V^{2}-2E_{\mathrm {b}}V\cos \delta } \\[ 5pt ]
I_{\mathrm {b}}&=&\frac {\sqrt {E_{\mathrm {b}}^{2}+V^{2}-2E_{\mathrm {b}}V\cos \delta }}{X_{\mathrm {b}}} \\[ 5pt ]
&=&\frac {\sqrt {1.341 \ 7^{2}+1.0^{2}-2\times 1.341 \ 7\times 1.0\times 0.894 \ 43}}{1.5} \\[ 5pt ]
&≒&0.421 \ 66 → 0.422 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。続いて,\( \ P_{\mathrm {b}}=VI_{\mathrm {b}}\cos \theta _{\mathrm {b}} \ \)であるから,\( \ \cos \theta _{\mathrm {b}} \ \)は,
\[
\begin{eqnarray}
\cos \theta _{\mathrm {b}}&=&\frac {P_{\mathrm {b}}}{VI_{\mathrm {b}}} \\[ 5pt ]
&=&\frac {0.4}{1.0\times 0.421 \ 66} \\[ 5pt ]
&≒&0.948 \ 63 → 0.949 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。さらに,\( \ \sin \theta _{\mathrm {b}} \ \)が,
\[
\begin{eqnarray}
\sin \theta _{\mathrm {b}}&=&\sqrt {1-\cos ^{2}\theta _{\mathrm {b}}} \\[ 5pt ]
&=&\sqrt {1-0.948 \ 63^{2}} \\[ 5pt ]
&≒&0.316 \ 39 \\[ 5pt ]
\end{eqnarray}
\]
であることから,\( \ Q_{\mathrm {b}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {b}}&=&VI_{\mathrm {b}}\sin \theta _{\mathrm {b}} \\[ 5pt ]
&=&1.0\times 0.421 \ 66 \times 0.316 \ 39 \\[ 5pt ]
&≒&0.133 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん