【問題】
【難易度】★★★☆☆(普通)
三相星形結線の円筒形同期発電機\( \ \mathrm {A} \ \)機及び\( \ \mathrm {B} \ \)機の\( \ 2 \ \)台が共通母線に接続され並列運転している。\( \ \mathrm {A} \ \)機は,定格容量\( \ 10000 \ \mathrm {kV\cdot A} \ \),定格電圧(線間電圧)\( \ 6600 \ \mathrm {V} \ \),定格力率\( \ 0.9 \ \)(遅れ),短絡比\( \ 0.5 \ \)であり,\( \ \mathrm {B} \ \)機は,定格容量,定格電圧及び定格力率が\( \ \mathrm {A} \ \)機と同じであるが,短絡比は\( \ 0.6 \ \)である。この並列運転に関して次の問に答えよ。ただし,鉄心の磁気飽和及び電機子抵抗は無視できるものとする。また,単位法は各機の定格容量\( \ \left( 10000 \ \mathrm {kV\cdot A} \right) \ \)及び定格電圧を基準とする。
(1) 各発電機における,次のa及びbの値を求めよ。
a.同期リアクタンス\( \ X_{\mathrm {SA}} \ \),\( \ X_{\mathrm {SB}} \ \mathrm {[p.u.]} \ \)
b.発電機定格出力運転時の無負荷誘導起電力\( \ E_{\mathrm {A}} \ \),\( \ E_{\mathrm {B}} \ \mathrm {[p.u.]} \ \)
(2) 両発電機が接続されている共通母線電圧(線間電圧)を定格電圧\( \ 6600 \ \mathrm {V} \ \)に保ち,両発電機の負荷への有効電力及び界磁電流を無負荷状態から徐々に増加させ,両発電機とも界磁電流は定格出力運転時の界磁電流(上記小問(1)bの値の無負荷誘導起電力\( \ E_{\mathrm {A}} \ \),\( \ E_{\mathrm {B}} \ \)に相当)まで到達した。各発電機の機械入力を調整して\( \ {\dot E}_{\mathrm {A}} \ \)及び\( \ {\dot E}_{\mathrm {B}} \ \)を同位相(内部相差角\( \ \delta _{\mathrm {A}}=\delta _{\mathrm {B}}=\delta \ \))にしながら,両発電機の負荷への合計有効電力を\( \ 16000 \ \mathrm {kW} \ \)にした。このときの内部相差角の\( \ \sin \delta \ \),各発電機が分担する有効電力\( \ P_{\mathrm {A}} \ \),\( \ P_{\mathrm {B}} \ \mathrm {[kW]} \ \),発電機\( \ \mathrm {A} \ \)機の相電流\( \ I_{\mathrm {A}} \ \mathrm {[p.u.]} \ \)及び力率(遅れ)\( \ \cos \phi _{\mathrm {A}} \ \)を算出せよ。なお,\( \ {\dot E}_{\mathrm {A}} \ \)又は\( \ {\dot E}_{\mathrm {B}} \ \)は大きさ\( \ E_{\mathrm {A}} \ \)又は\( \ E_{\mathrm {B}} \ \)のフェーザである。
【ワンポイント解説】
(1)の難易度が易しめで(2)が標準的な問題となります。他の問題を解いた後,時間がない時は本問の(1)だけ解き,部分点狙いをしても良いと思います。
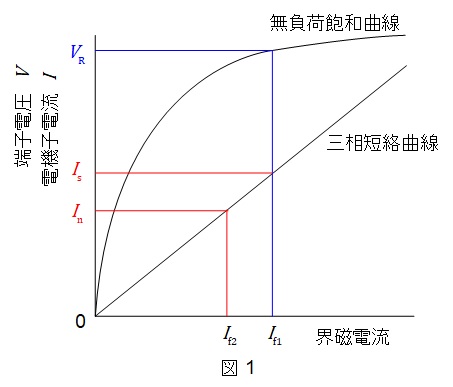
1.短絡比\(K_{\mathrm {s}}\)と単位法で表した同期インピーダンス\(Z_{\mathrm {s}}\)との関係
同期電動機の特性曲線は図1のように描けられ,短絡比\(K_{\mathrm {s}}\)は次のように定義されます。
\[
\begin{eqnarray}
K_{\mathrm {s}} &=& \frac {I_{\mathrm {f1}}}{I_{\mathrm {f2}}} \\[ 5pt ]
&=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ]
\end{eqnarray}
\]
短絡比\(K_{\mathrm {s}}\)と単位法で表した同期インピーダンス\(Z_{\mathrm {s}}\)との関係は,
\[
\begin{eqnarray}
K_{\mathrm {s}} &=& \frac {I_{\mathrm {s}}}{I_{\mathrm {n}}} \\[ 5pt ]
&=& \frac {\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}}}}{I_{\mathrm {n}}} \\[ 5pt ]
&=& \frac {V_{\mathrm {n}}}{\sqrt {3}Z_{\mathrm {s}}I_{\mathrm {n}}}\\[ 5pt ]
&=& \frac {1}{Z_{\mathrm {s}}\mathrm {[p.u.]}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.同期発電機の送電電力\( \ P \ \)
誘導起電力が\( \ E \ \),端子電圧が\( \ V \ \)であり,内部相差角が\( \ \delta \ \),同期インピーダンスが\( \ X \ \)の時の同期発電機の送電電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\frac {EV}{X}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となります。
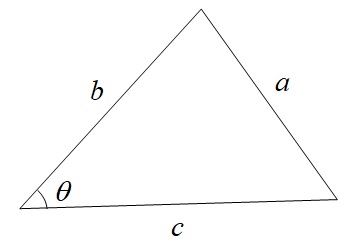
3.余弦定理
下図のような三角形において,
\[
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
の関係が成立します。
【解答】
(1)a.同期リアクタンス\( \ X_{\mathrm {SA}} \ \),\( \ X_{\mathrm {SB}} \ \mathrm {[p.u.]} \ \)
ワンポイント解説「1.短絡比\(K_{\mathrm {s}}\)と単位法で表した同期インピーダンス\(Z_{\mathrm {s}}\)との関係」の通り,単位法で表した同期リアクタンス\( \ X_{\mathrm {SA}} \ \),\( \ X_{\mathrm {SB}} \ \mathrm {[p.u.]} \ \)は短絡比の逆数であるから,
\[
\begin{eqnarray}
X_{\mathrm {SA}} &=& \frac {1}{K_{\mathrm {SA}}} \\[ 5pt ]
&=& \frac {1}{0.5} \\[ 5pt ]
&=& 2.00 \ \mathrm {[p.u.]} \\[ 5pt ]
X_{\mathrm {SB}} &=& \frac {1}{K_{\mathrm {SB}}} \\[ 5pt ]
&=& \frac {1}{0.6} \\[ 5pt ]
&≒& 1.6667 → 1.67 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(1)b.発電機定格出力運転時の無負荷誘導起電力\( \ E_{\mathrm {A}} \ \),\( \ E_{\mathrm {B}} \ \mathrm {[p.u.]} \ \)
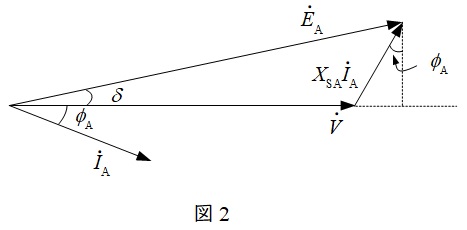
題意に沿って\( \ \mathrm {A} \ \)機のベクトル図を描くと図2のようになる。
題意より,\( \ V=1 \ \mathrm {[p.u.]} \ \),\( \ \cos \phi _{\mathrm {A}}=0.9 \ \)であるから,図2より,
\[
\begin{eqnarray}
E_{\mathrm {A}} &=& \sqrt {\left( V+X_{\mathrm {SA}}I_{\mathrm {A}}\sin \phi _{\mathrm {A}} \right) ^{2}+\left( X_{\mathrm {SA}}I_{\mathrm {A}}\cos \phi _{\mathrm {A}} \right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,
\[
\begin{eqnarray}
\sin \phi _{\mathrm {A}} &=& \sqrt {1-\cos ^{2}\phi _{\mathrm {A}}} \\[ 5pt ]
&=& \sqrt {1-0.9 ^{2}} \\[ 5pt ]
&≒& 0.43589 \\[ 5pt ]
\end{eqnarray}
\]
であるから,各値を代入すると,
\[
\begin{eqnarray}
E_{\mathrm {A}} &=& \sqrt {\left( 1+2\times 1 \times 0.43589 \right) ^{2}+\left( 2\times 1 \times 0.9 \right) ^{2}} \\[ 5pt ]
&≒& 2.5968 → 2.60 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。同様に,
\[
\begin{eqnarray}
E_{\mathrm {B}} &=& \sqrt {\left( V+X_{\mathrm {SB}}I_{\mathrm {B}}\sin \phi _{\mathrm {B}} \right) ^{2}+\left( X_{\mathrm {SB}}I_{\mathrm {B}}\cos \phi _{\mathrm {B}} \right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,各値を代入すると,
\[
\begin{eqnarray}
E_{\mathrm {B}} &=& \sqrt {\left( 1+1.6667\times 1 \times 0.43589 \right) ^{2}+\left( 1.6667 \times 1 \times 0.9 \right) ^{2}} \\[ 5pt ]
&≒& 2.2871 → 2.29 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)同期運転時の内部相差角の\( \ \sin \delta \ \),各発電機が分担する有効電力\( \ P_{\mathrm {A}} \ \),\( \ P_{\mathrm {B}} \ \mathrm {[kW]} \ \),発電機\( \ \mathrm {A} \ \)機の相電流\( \ I_{\mathrm {A}} \ \mathrm {[p.u.]} \ \)及び力率(遅れ)\( \ \cos \phi _{\mathrm {A}} \ \)
ワンポイント解説「2.同期発電機の送電電力\( \ P \ \)」より,\( \ \mathrm {A} \ \)機及び\( \ \mathrm {B} \ \)機の\( \ 2 \ \)台が並列運転している際の送電電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\frac {E_{\mathrm {A}}V}{X_{\mathrm {SA}}}\sin \delta +\frac {E_{\mathrm {B}}V}{X_{\mathrm {SB}}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
である。有効電力を単位法で表すと,
\[
\begin{eqnarray}
P \ \mathrm {[p.u.]} &=& \frac {P \ \mathrm {[kW]}}{P_{\mathrm {n}}} \\[ 5pt ]
&=& \frac {16000}{10000} \\[ 5pt ]
&=& 1.6 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,各値を代入すると,
\[
\begin{eqnarray}
1.6&=&\frac {2.5968\times 1}{2}\sin \delta +\frac {2.2871\times 1}{1.6667}\sin \delta \\[ 5pt ]
\sin \delta &=&\frac {1.6}{\displaystyle \frac {2.5968\times 1}{2}+\frac {2.2871\times 1}{1.6667}} \\[ 5pt ]
&≒&0.59911 → 0.599 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって,各発電機が分担する有効電力\( \ P_{\mathrm {A}} \ \),\( \ P_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {A}}&=&\frac {E_{\mathrm {A}}V}{X_{\mathrm {SA}}}\sin \delta \\[ 5pt ]
&=&\frac {2.5968\times 1}{2}\times 0.59911 \\[ 5pt ]
&≒&0.77788 \ \mathrm {[p.u.]} \\[ 5pt ]
P_{\mathrm {B}}&=&\frac {E_{\mathrm {B}}V}{X_{\mathrm {SB}}}\sin \delta \\[ 5pt ]
&=&\frac {2.2871\times 1}{1.6667}\times 0.59911 \\[ 5pt ]
&≒&0.82212 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので、\( \ \mathrm {kW} \ \)に変換すると,
\[
\begin{eqnarray}
P_{\mathrm {A}}&=&10000 \times 0.77788 \\[ 5pt ]
&=&7778.8 → 7780 \ \mathrm {[kW]} \\[ 5pt ]
P_{\mathrm {B}}&=&10000 \times 0.82212\\[ 5pt ]
&=&8221.2 → 8220 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
図2のベクトル図の三角形にワンポイント解説「3.余弦定理」の通り,余弦定理を適用すると,
\[
\begin{eqnarray}
\left( X_{\mathrm {SA}}I_{\mathrm {A}}\right) ^{2} &=& E_{\mathrm {A}}^{2}+V^{2}-2E_{\mathrm {A}}V\cos \delta \\[ 5pt ]
X_{\mathrm {SA}}I_{\mathrm {A}} &=& \sqrt {E_{\mathrm {A}}^{2}+V^{2}-2E_{\mathrm {A}}V\cos \delta } \\[ 5pt ]
I_{\mathrm {A}} &=&\frac { \sqrt {E_{\mathrm {A}}^{2}+V^{2}-2E_{\mathrm {A}}V\cos \delta }}{X_{\mathrm {SA}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
\cos \delta &=& \sqrt {1-\sin ^{2} \delta } \\[ 5pt ]
&=& \sqrt {1-0.59911 ^{2} } \\[ 5pt ] \\[ 5pt ]
&≒&0.80067 \\[ 5pt ]
\end{eqnarray}
\]
であるので,各値を代入すると,
\[
\begin{eqnarray}
I_{\mathrm {A}} &=&\frac { \sqrt {2.5968 ^{2}+1^{2}-2\times 2.5968 \times 1 \times 0.80067 }}{2} \\[ 5pt ]
&≒&0.94671 → 0.947 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。さらに,\( \ P_{\mathrm {A}}=VI_{\mathrm {A}}\cos \phi _{\mathrm {A}} \ \)であるから,
\[
\begin{eqnarray}
\cos \phi _{\mathrm {A}} &=&\frac { P_{\mathrm {A}}}{VI_{\mathrm {A}}} \\[ 5pt ]
&=&\frac {0.77788}{1\times 0.94671} \\[ 5pt ]
&≒&0.82167 → 0.822 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん