【問題】
【難易度】★★☆☆☆(やや易しい)
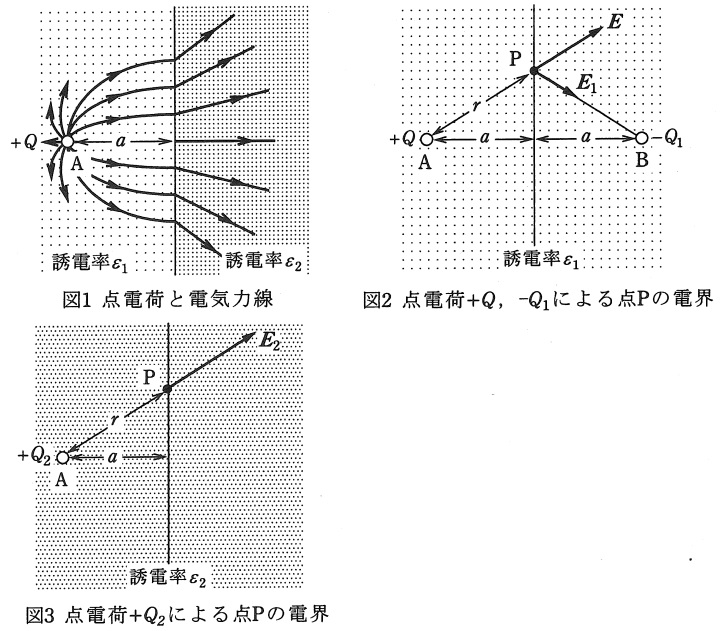
次の文章は,二つの誘電体が平面で接しているとき,一方の誘電体中にある点電荷と他方の誘電体との間の力に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式を解答群の中から選び,その記号を記述用紙の解答欄に記入しなさい。なお,図1は誘電体中の点電荷と電気力線の概略図を表した図である。また,図2,図3は影像電荷による電界を示す。
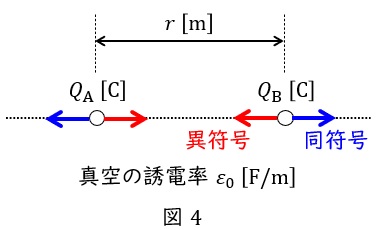
図1のように,誘電率が\( \ \varepsilon _{1} \ \)と\( \ \varepsilon _{2} \ \)\(\left( \ \varepsilon _{2}>\varepsilon _{1} \right.\)とする\(\left. \right) \ \)の誘電体が無限に広がる平面で接しているとする。境界面から距離が\( \ a \ \)である点\( \ \mathrm {A} \ \)に点電荷\( \ +Q \ \)が存在しているときに境界面での電束密度,電位を考える。この場合,誘電率が\( \ \varepsilon _{1} \ \)の誘電体内の電界は,境界面に関する点\( \ \mathrm {A} \ \)の影像点を点\( \ \mathrm {B} \ \)としたとき,図2のように全空間が\( \ \varepsilon _{1} \ \)の誘電体で満たされているとして,点\( \ \mathrm {A} \ \),点\( \ \mathrm {B} \ \)にそれぞれ点電荷\( \ +Q \ \),未知の点電荷\( \ -Q_{1} \ \)がある場合の電界に等しい。図2で,点\( \ \mathrm {A} \ \),点\( \ \mathrm {B} \ \)から距離が\( \ r \ \)である境界面上の点\( \ \mathrm {P} \ \)の\( \ +Q \ \),\( \ -Q_{1} \ \)の点電荷による電界をそれぞれ\( \ \boldsymbol E \ \)(ベクトル),\( \ \boldsymbol E_{1} \ \)(ベクトル)とする。この場合,点\( \ \mathrm {P} \ \)の電位\( \ V_{p1} \ \)は\( \ \fbox { (1) } \ \)である。また,この点における電束密度の境界面に垂直な成分\( \ D_{h1} \ \)は\( \ \fbox { (2) } \ \)である。
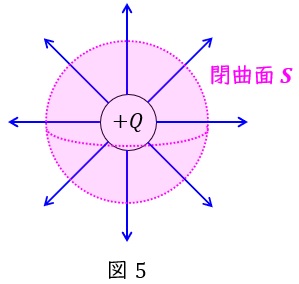
次に,図1の\( \ \varepsilon _{2} \ \)の誘電体内の電界は図3のように全空間が\( \ \varepsilon _{2} \ \)の誘電体で満たされているとし,点\( \ \mathrm {A} \ \)に未知の点電荷\( \ +Q_{2} \ \)があるとしたときの電界\( \ \boldsymbol E_{2} \ \)(ベクトル)に等しい。この場合,点\( \ \mathrm {P} \ \)の電束密度で,境界面に垂直な成分\( \ D_{h2} \ \)は\( \ \fbox { (3) } \ \)である。ここで,未知量 \( \ Q_{1} \ \),\( \ Q_{2} \ \)は次の境界条件によって求めることができる。すなわち,境界面で電束は連続でなければならないから\( \ D_{h1}=D_{h2} \ \)である。また,境界面で電位は連続でなければならない。
この二つの条件から\( \ Q_{1} \ \)及び\( \ Q_{2} \ \)は\( \ \fbox { (4) } \ \)となる。また,点\( \ \mathrm {A} \ \)にある点電荷\( \ +Q \ \)と誘電率\( \ \varepsilon _{2} \ \)の誘電体との間の力の大きさは点電荷\( \ +Q \ \)と\( \ -Q_{1} \ \)との間の力\( \ F \ \)の大きさに等しい。したがって,その力の大きさは\( \ \fbox { (5) } \ \)となる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {Q_{2}a}{4\pi r^{2}} &(ロ)& \frac {Q-Q_{1}}{4\pi \varepsilon _{1}r} &(ハ)& \frac {Q+Q_{1}}{4\pi r^{2}} \\[ 5pt ]
&(ニ)& \frac {\left( Q+Q_{1}\right) a}{4\pi r^{3}} &(ホ)& \frac {Q+Q_{1}}{4\pi \varepsilon _{1}r} &(ヘ)& \left| \frac {\left( \varepsilon _{1}-\varepsilon _{2}\right) Q^{2}}{8\pi \varepsilon _{1}\left( \varepsilon _{1}+\varepsilon _{2}\right) a^{2}}\right| \\[ 5pt ]
&(ト)& \frac {Q_{2}a}{4\pi r^{3}} &(チ)& \frac {Q_{2}}{4\pi r^{2}} &(リ)& \left| \frac {\left( \varepsilon _{1}-\varepsilon _{2}\right) Q^{2}}{16\pi \varepsilon _{1}\left( \varepsilon _{1}+\varepsilon _{2}\right) a^{2}}\right| \\[ 5pt ]
&(ヌ)& \left| \frac {\left( \varepsilon _{1}+\varepsilon _{2}\right) Q^{2}}{16\pi \varepsilon _{1}\left( \varepsilon _{1}-\varepsilon _{2}\right) a^{2}}\right| &(ル)& \frac {Q+Q_{1}}{4\pi \varepsilon _{1}r^{2}} &(ヲ)& \frac {Q-Q_{1}}{4\pi r^{2}} \\[ 5pt ]
&(ワ)& \left\{
\begin{array}{l}
Q_{1} =\displaystyle \frac {\varepsilon _{1}+\varepsilon _{2}}{\varepsilon _{1}-\varepsilon _{2}}Q \\[ 5pt ]
Q_{2} =\displaystyle \frac {2\varepsilon _{2}}{\varepsilon _{1}-\varepsilon _{2}}Q
\end{array}
\right. &(カ)& \left\{
\begin{array}{l}
Q_{1} =\displaystyle \frac {\varepsilon _{1}-\varepsilon _{2}}{\varepsilon _{1}+\varepsilon _{2}}Q \\[ 5pt ]
Q_{2} =\displaystyle \frac {\varepsilon _{2}}{\varepsilon _{1}+\varepsilon _{2}}Q
\end{array}
\right. &(ヨ)& \left\{
\begin{array}{l}
Q_{1} =\displaystyle \frac {\varepsilon _{2}-\varepsilon _{1}}{\varepsilon _{1}+\varepsilon _{2}}Q \\[ 5pt ]
Q_{2} =\displaystyle \frac {2\varepsilon _{2}}{\varepsilon _{1}-\varepsilon _{2}}Q
\end{array}
\right. \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
\( \ 2 \ \)種類の誘電体を接したときの各諸量を仮想電荷により求める問題です。
一見複雑に見えますが,文中に導出方法が指定されており,公式も\( \ 2 \ \)種までに学習した内容で占められていますので,落ち着いて解けば十分完答を狙える問題かと思います。
平成21年は前半にやや難易度が高めの問題が設定されていたため,配点の高い本問は合否を分ける非常に重要な問題とも言えるでしょう。
1.クーロンの法則
真空中で距離\( \ r \ \mathrm {[m]} \ \)離れた二つの電荷\( \ Q_{\mathrm {A}} \ \mathrm {[C]} \ \),\( \ Q_{\mathrm {B}} \ \mathrm {[C]} \ \)に加わる力\( \ F \ \mathrm {[N]} \ \)は,真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \)とすると,
\[
\begin{eqnarray}
F &=&\frac {Q_{\mathrm {A}}Q_{\mathrm {B}}}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。このとき,\( \ Q_{\mathrm {A}} \ \),\( \ Q_{\mathrm {B}} \ \)の\( \ + \ \)\( \ – \ \)の符号が同符号である場合には斥力(反発する力),異符号である場合には引力(引き合う力)が働きます。
2.ガウスの定理
\( \ Q \ \mathrm {[C]} \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本,電束は\( \ Q \ \)本であり,電界\( \ E \ \mathrm {[V / m]} \ \)及び電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ]
\end{eqnarray}
\]
となり,これをガウスの定理といいます。閉曲面が球で,点電荷に蓄えられている電荷\( \ Q \ \mathrm {[C]} \ \)があれば,電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
4\pi r^{2} \cdot E &=& \frac {Q}{\varepsilon } \\[ 5pt ]
E &=& \frac {Q}{4\pi \varepsilon r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.空間上の電位\( \ V \ \)
中心からの距離\( \ r \ \mathrm {[m]} \ \)に関する電界\( \ E_{\mathrm {r}} \ \mathrm {[V / m]} \ \)が与えられている時,その場所の電位\( \ V \ \mathrm {[V]} \ \)は無限遠を基準とすると,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
\end{eqnarray}
\]
で求められます。これを電界\( \ \displaystyle E = \frac {Q}{4\pi \varepsilon r^{2}} \ \)に適用すると,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}\frac {Q}{4\pi \varepsilon r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {Q}{4\pi \varepsilon }\int _{\infty }^{r}\frac {1}{r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {Q}{4\pi \varepsilon }\left[ -\frac {1}{r}\right] _{\infty }^{r} \\[ 5pt ]
&=&-\frac {Q}{4\pi \varepsilon }\left( -\frac {1}{r}\right) \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon r} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 3 \ \)種で学習する公式と同じとなります。
【解答】
(1)解答:ロ
図2において,点\( \ \mathrm {A} \ \)の電荷\( \ +Q \ \)及び点\( \ \mathrm {B} \ \)の電荷\( \ -Q_{1} \ \)より,点\( \ \mathrm {P} \ \)の電位\( \ V_{p1} \ \)は,ワンポイント解説「3.空間上の電位\( \ V \ \)」の通り,
\[
\begin{eqnarray}
V_{p1}&=&\frac {Q}{4\pi \varepsilon _{1}r}-\frac {Q_{1}}{4\pi \varepsilon _{1}r} \\[ 5pt ]
&=&\frac {Q-Q_{1}}{4\pi \varepsilon _{1}r} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
点\( \ \mathrm {A} \ \)の電荷\( \ +Q \ \)による点\( \ \mathrm {P} \ \)おける電束密度\( \ D_{1A} \ \)は,ワンポイント解説「2.ガウスの定理」の通り,
\[
\begin{eqnarray}
4\pi r^{2} D_{1A} &=& Q \\[ 5pt ]
D_{1A} &=& \frac {Q}{4\pi r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,境界面に垂直な成分\( \ D_{h1A} \ \)は,
\[
\begin{eqnarray}
D_{h1A} &=& D_{1A}\times \frac {a}{r} \\[ 5pt ]
&=& \frac {Q}{4\pi r^{2}}\times \frac {a}{r} \\[ 5pt ]
&=& \frac {Qa}{4\pi r^{3}} \\[ 5pt ]
\end{eqnarray}
\]
となる。同様に,点\( \ \mathrm {B} \ \)の電荷\( \ -Q_{1} \ \)による点\( \ \mathrm {P} \ \)における電束密度の境界面に垂直な成分\( \ D_{h1B} \ \)は,
\[
\begin{eqnarray}
D_{h1B} &=& \frac {Q_{1}a}{4\pi r^{3}} \\[ 5pt ]
\end{eqnarray}
\]
となる。図2より,\( \ D_{h1A} \ \)と\( \ D_{h1B} \ \)は同方向なので,点\( \ \mathrm {P} \ \)における電束密度の境界面に垂直な成分\( \ D_{h1} \ \)は,
\[
\begin{eqnarray}
D_{h1} &=&D_{h1A}+D_{h1B} \\[ 5pt ]
&=&\frac {Qa}{4\pi r^{3}}+\frac {Q_{1}a}{4\pi r^{3}} \\[ 5pt ]
&=&\frac {\left( Q+Q_{1}\right) a}{4\pi r^{3}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ト
(2)と同様に考えれば,図3において点\( \ \mathrm {P} \ \)の電束密度の境界面に垂直な成分\( \ D_{h2} \ \)は,
\[
\begin{eqnarray}
D_{h2} &=& \frac {Q_{2}a}{4\pi r^{3}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
(1)と同様に,図3における点\( \ \mathrm {P} \ \)の電位\( \ V_{p2} \ \)は,
\[
\begin{eqnarray}
V_{p2}&=&\frac {Q_{2}}{4\pi \varepsilon _{2}r} \\[ 5pt ]
\end{eqnarray}
\]
である。\( \ D_{h1}=D_{h2} \ \)より,
\[
\begin{eqnarray}
\frac {\left( Q+Q_{1}\right) a}{4\pi r^{3}}&=& \frac {Q_{2}a}{4\pi r^{3}} \\[ 5pt ]
Q+Q_{1}&=& Q_{2} ・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ V_{p1}=V_{p2} \ \)より,
\[
\begin{eqnarray}
\frac {Q-Q_{1}}{4\pi \varepsilon _{1}r}&=&\frac {Q_{2}}{4\pi \varepsilon _{2}r} \\[ 5pt ]
\frac {Q-Q_{1}}{\varepsilon _{1}}&=&\frac {Q_{2}}{\varepsilon _{2}} \\[ 5pt ]
Q-Q_{1} &=&\frac {\varepsilon _{1}}{\varepsilon _{2}}Q_{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。これに①を代入すると,
\[
\begin{eqnarray}
Q-Q_{1} &=&\frac {\varepsilon _{1}}{\varepsilon _{2}}\left( Q+Q_{1}\right) \\[ 5pt ]
\varepsilon _{2}Q-\varepsilon _{2}Q_{1}&=&\varepsilon _{1}Q+\varepsilon _{1}Q_{1} \\[ 5pt ]
\varepsilon _{1}Q_{1}+\varepsilon _{2}Q_{1}&=&\varepsilon _{2}Q-\varepsilon _{1}Q \\[ 5pt ]
\left( \varepsilon _{1}+\varepsilon _{2}\right) Q_{1}&=&\left( \varepsilon _{2}-\varepsilon _{1}\right) Q \\[ 5pt ]
Q_{1}&=&\frac {\varepsilon _{2}-\varepsilon _{1}}{\varepsilon _{1}+\varepsilon _{2}}Q \\[ 5pt ]
\end{eqnarray}
\]
と求められ,さらに上式を①に代入すると,
\[
\begin{eqnarray}
Q_{2}&=& Q+\frac {\varepsilon _{2}-\varepsilon _{1}}{\varepsilon _{1}+\varepsilon _{2}}Q \\[ 5pt ]
&=& \frac {\varepsilon _{1}+\varepsilon _{2}+\varepsilon _{2}-\varepsilon _{1}}{\varepsilon _{1}+\varepsilon _{2}}Q \\[ 5pt ]
&=& \frac {2\varepsilon _{2}}{\varepsilon _{1}-\varepsilon _{2}}Q \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:リ
(4)解答式及びワンポイント解説「1.クーロンの法則」より,点電荷\( \ +Q \ \)と\( \ -Q_{1} \ \)との間の力\( \ F \ \)の大きさは,
\[
\begin{eqnarray}
F &=&\left| \frac {Q\left(-Q_{\mathrm {1}}\right) }{4\pi \varepsilon _{1}\left( 2a\right) ^{2}}\right| \\[ 5pt ]
&=&\left| \frac {\displaystyle Q\left( -\frac {\varepsilon _{2}-\varepsilon _{1}}{\varepsilon _{1}+\varepsilon _{2}}Q\right) }{16\pi \varepsilon _{1}a^{2}}\right| \\[ 5pt ]
&=&\left| \frac {\left( \varepsilon _{1}-\varepsilon _{2}\right) Q^{2}}{16\pi \varepsilon _{1}\left( \varepsilon _{1}+\varepsilon _{2}\right) a^{2}}\right| \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん