《理論》〈電子理論〉[H25:問7] 演算増幅器を用いた回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

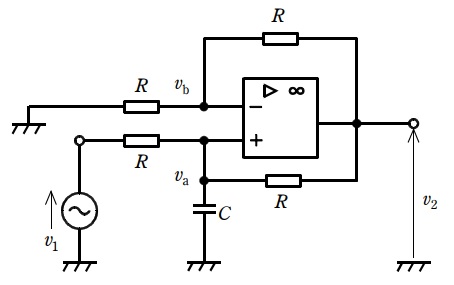
次の文章は，演算増幅器を用いた回路に関するに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。ただし，すべての抵抗の値は等しく，$ \ R \ $とし，また，入力信号源$ \ v_{1} \ $は角周波数$ \ \omega \left( \omega ＞0 \right) \ $の正弦波電圧源である。

図の回路において，演算増幅器の入力端子には電流が流れ込まないことから非反転入力端子の電位$ \ v_{\mathrm {a}} \ $は
\[
\begin{eqnarray}
v_{\mathrm {a}} &=& \fbox {　（１）　} \ \left( v_{1}+v_{2}\right) \\[ 5pt ] \end{eqnarray}
\] であり，$ \ v_{2} \ $は
\[
\begin{eqnarray}
v_{2} &=& \fbox {　（２）　} \ v_{\mathrm {b}} \\[ 5pt ] \end{eqnarray}
\] となる。また，演算増幅器の性質から$ \ v_{\mathrm {a}}=v_{\mathrm {b}} \ $なので，$ \ v_{2} \ $を
\[
\begin{eqnarray}
v_{2} &=& \fbox {　（３）　} \ v_{1} \\[ 5pt ] \end{eqnarray}
\] と求めることができる。

$ \ \fbox {　（３）　} \ $の偏角は$ \ \fbox {　（４）　} \ [°] \ $であり，$ \ \fbox {　（３）　} \ $の絶対値が$ \ 1 \ $となる角周波数$ \ \omega \ $は$ \ \fbox {　（５）　} \ $である。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {-1}{2+\mathrm {j}\omega CR}　　&（ロ）&　2　　&（ハ）&　\frac {1}{2+\mathrm {j}\omega CR} \\[ 5pt ] &（ニ）&　90　　　&（ホ）&　\frac {1}{CR}　　　&（ヘ）&　-90 \\[ 5pt ] &（ト）&　\frac {1}{1+\mathrm {j}2\omega CR}　　　&（チ）&　\frac {1}{\mathrm {j}2\omega CR}　　　&（リ）&　\frac {2}{\mathrm {j}\omega CR} \\[ 5pt ] &（ヌ）&　-45　　　&（ル）&　\frac {1}{\mathrm {j}\omega CR}　　　&（ヲ）&　\frac {1}{2CR} \\[ 5pt ] &（ワ）&　1　　　&（カ）&　\frac {2}{CR}　　　&（ヨ）&　\frac {1}{2} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

演算増幅器の特性を問う問題となっています。基本は$ \ 2 \ $種や$ \ 3 \ $種の頃と同じです。$ \ 1 \ $種としては易しい問題と言えると思います。

1.理想的な演算増幅器の特徴
１．電圧増幅率が無限大です。したがって，無限大でない有限数が出力される時，入力端子間の電圧は0 V(バーチャルショート)となります。
２．入力インピーダンスが無限大です。したがって入力端子に電流は流れません。
３．出力インピーダンスがゼロです。

【解答】

(1)解答：ハ
$ \ + \ $側入力端子に電流が流れないので，$ \ v_{\mathrm {a}} \ $部の回路方程式は，
\[
\begin{eqnarray}
\mathrm {j}\omega C v_{\mathrm {a}}&=& \frac {v_{1}-v_{\mathrm {a}}}{R}+\frac {v_{2}-v_{\mathrm {a}}}{R} \\[ 5pt ] \mathrm {j}\omega CR v_{\mathrm {a}}&=& v_{1}+v_{2}-2v_{\mathrm {a}} \\[ 5pt ] \left( 2+\mathrm {j}\omega CR \right) v_{\mathrm {a}}&=& v_{1}+v_{2} \\[ 5pt ] v_{\mathrm {a}}&=& \frac {1}{2+\mathrm {j}\omega CR}\left( v_{1}+v_{2}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ロ
$ \ – \ $側入力端子にも電流は流れないので，
\[
\begin{eqnarray}
\frac {v_{\mathrm {b}}}{R}&=& \frac {v_{2}-v_{\mathrm {b}}}{R} \\[ 5pt ] v_{\mathrm {b}}&=& v_{2}-v_{\mathrm {b}} \\[ 5pt ] v_{2}&=& 2v_{\mathrm {b}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：リ
(1)，(2)の解答式より，
\[
\begin{eqnarray}
\frac {1}{2+\mathrm {j}\omega CR}\left( v_{1}+v_{2}\right) &=& \frac {v_{2}}{2} \\[ 5pt ] 2\left( v_{1}+v_{2}\right) &=& v_{2}\left( 2+\mathrm {j}\omega CR\right) \\[ 5pt ] 2v_{1} &=& \mathrm {j}\omega CRv_{2} \\[ 5pt ] v_{2} &=& \frac {2}{\mathrm {j}\omega CR}v_{1} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヘ
(3)の解答式を変形すると，
\[
\begin{eqnarray}
v_{2} &=& -\mathrm {j}\frac {2}{\omega CR}v_{1} \\[ 5pt ] \end{eqnarray}
\] となるので，絶対値が$ \ \displaystyle \frac {2}{\omega CR} \ $，偏角は$ \ -90 \ [°] \ $となる。

(5)解答：カ
絶対値が$ \ 1 \ $となる角周波数は，
\[
\begin{eqnarray}
\frac {2}{\omega CR} &=& 1 \\[ 5pt ] \omega &=& \frac {2}{CR} \\[ 5pt ] \end{eqnarray}
\] と求められる。