《理論》〈電子理論〉[H21:問7]バイポーラトランジスタを用いた増幅回路に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

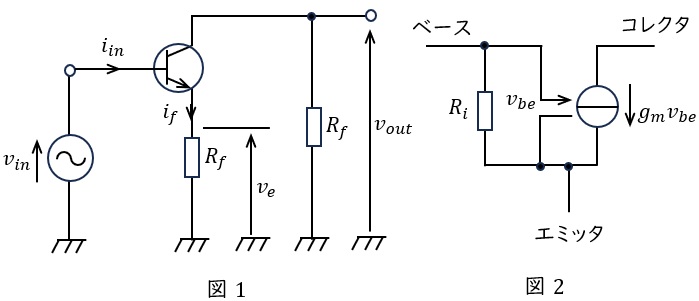
次の文章は，図1に示すバイポーラトランジスタを用いた増幅回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式を解答群の中から選び，その記号を記述用紙の解答欄に記入しなさい。ただし，図1は，増幅回路の交流成分のみを考慮しており，バイポーラトランジスタの交流等価回路は図2で表されるものとする。

\( \ R_{f} \ \)が\( \ 0 \ \mathrm {[\Omega ]} \ \)のとき，図1の増幅回路の入力抵抗は\( \ \displaystyle \frac {v_{in}}{i_{in}}= \ \fbox {　 （１） 　} \ \)であり，電圧利得は\( \ \displaystyle \frac {v_{out}}{v_{in}}=-g_{m}R_{L} \ \)である。

次に，\( \ R_{f} \ \)が\( \ 0 \ \mathrm {[\Omega ]} \ \)でなく，正の値のときを考える。バイポーラトランジスタのベース・エミッタ間の抵抗\( \ R_{i} \ \)に流れる電流は，電流源\( \ g_{m}v_{be} \ \)の電流よりも十分小さく無視できるものとすると，
\[
\begin{eqnarray}
i_{f}&=&g_{m}\times \left( \ \fbox {　 （２） 　} \ \right) \\[ 5pt ] \end{eqnarray}
\] と表すことができる。また，\( \ v_{e}=R_{f}i_{f} \ \)なので
\[
\begin{eqnarray}
v_{e}&=& \ \fbox {　 （３） 　} \ \times v_{in} \\[ 5pt ] \end{eqnarray}
\] となる。これらの結果を使うと，電圧利得\( \ \displaystyle \frac {v_{out}}{v_{in}} \ \)が求められる。\( \ A=g_{m}R_{L} \ \)とおくと，電圧利得は
\[
\begin{eqnarray}
\frac {v_{out}}{v_{in}}&=& \frac {-A}{1+AH} \\[ 5pt ] \end{eqnarray}
\] と表される。ただし，
\[
\begin{eqnarray}
H&=& \ \fbox {　 （４） 　} \ \\[ 5pt ] \end{eqnarray}
\] である。さらに，\( \ \displaystyle i_{in}=\frac { \ \fbox {　 （２） 　} \ }{R_{i}} \ \)であるので，入力抵抗は
\[
\begin{eqnarray}
\frac {v_{in}}{i_{in}}&=&R_{i}\times \left( \ \fbox {　 （５） 　} \ \right) \\[ 5pt ] \end{eqnarray}
\] となる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　-1+AH　　　　　&（ロ）&　1-AH　　　　　&（ハ）&　\frac {g_{m}R_{L}}{1+g_{m}R_{f}} \\[ 5pt ] &（ニ）&　v_{e}-v_{out}　　　　　&（ホ）&　\frac {g_{m}R_{f}}{1+g_{m}R_{f}}　　　　　&（ヘ）&　R_{f} \\[ 5pt ] &（ト）&　v_{in}-v_{e}　　　　　&（チ）&　\frac {R_{f}}{R_{L}}　　　　　&（リ）&　\frac {R_{i}}{R_{L}} \\[ 5pt ] &（ヌ）&　\frac {R_{L}}{R_{f}}　　　　　&（ル）&　v_{in}-v_{out}　　　　　　&（ヲ）&　R_{L} \\[ 5pt ] &（ワ）&　\frac {g_{m}R_{i}}{1+g_{m}R_{f}}　　　　　&（カ）&　R_{i}　　　　　 &（ヨ）&　1+AH \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

バイポーラトランジスタの交流成分の等価回路から各演算を行う問題です。
キルヒホッフの法則等の基本的な電気回路の公式以外は使用しませんが，受験生によっては苦手とされている受験生も多いです。
まず，図3や図4に記載されているように，全体の回路を記載し回路計算を行うと解ける場合が多いかと思います。

【解答】

(1)解答：カ
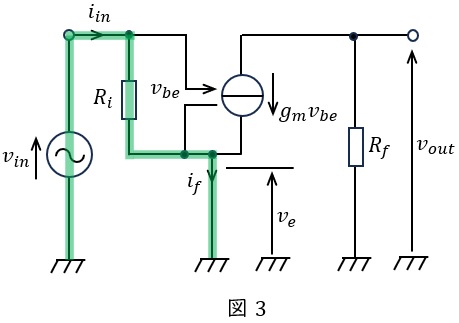
\( \ R_{f} = 0 \ \mathrm {[\Omega ]} \ \)のとき，図1と図2を組み合わせた回路は図3のようになる。
図3に示す閉回路にキルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
v_{in}&=&R_{i}i_{in} \\[ 5pt ] \frac {v_{in}}{i_{in}}&=&R_{i} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ト
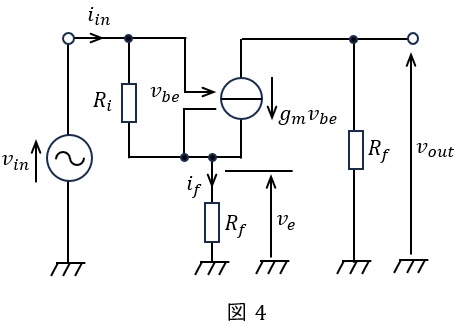
\( \ R_{f} ＞ 0 \ \mathrm {[\Omega ]} \ \)のとき，図1と図2を組み合わせた回路は図4のようになる。
題意より，バイポーラトランジスタのベース・エミッタ間の抵抗\( \ R_{i} \ \)に流れる電流は，電流源\( \ g_{m}v_{be} \ \)の電流よりも十分小さく無視できるとなっているので，\( \ i_{f} \ \)は，
\[
\begin{eqnarray}
i_{f}&≃&g_{m}v_{be} \\[ 5pt ] &=&g_{m} \left( v_{in}-v_{e}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ホ
(2)解答式を\( \ v_{e}=R_{f}i_{f} \ \)に代入すれば，
\[
\begin{eqnarray}
v_{e}&=&R_{f}\times g_{m}\left( v_{in}-v_{e}\right) \\[ 5pt ] v_{e}&=&g_{m}R_{f}v_{in}-g_{m}R_{f}v_{e} \\[ 5pt ] v_{e}+g_{m}R_{f}v_{e}&=&g_{m}R_{f}v_{in} \\[ 5pt ] \left( 1+g_{m}R_{f}\right) v_{e}&=&g_{m}R_{f}v_{in} \\[ 5pt ] v_{e}&=&\frac {g_{m}R_{f}}{1+g_{m}R_{f}}v_{in} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：チ
図4より，
\[
\begin{eqnarray}
v_{out}&=&-g_{m}v_{be}R_{L} \\[ 5pt ] &=&-Av_{be} \\[ 5pt ] &=&-A\left( v_{in}-v_{e}\right) \\[ 5pt ] &=&-A\left( v_{in}-\frac {g_{m}R_{f}}{1+g_{m}R_{f}}v_{in}\right) \\[ 5pt ] &=&-A\left( 1-\frac {g_{m}R_{f}}{1+g_{m}R_{f}}\right)v_{in} \\[ 5pt ] \frac {v_{out}}{v_{in}}&=&-A\left( 1-\frac {g_{m}R_{f}}{1+g_{m}R_{f}}\right) \\[ 5pt ] &=&-A\cdot \frac {1+g_{m}R_{f}-g_{m}R_{f}}{1+g_{m}R_{f}} \\[ 5pt ] &=& \frac {-A}{1+g_{m}R_{f}} \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ \displaystyle \frac {-A}{1+AH} \ \)と比較すれば，
\[
\begin{eqnarray}
\frac {-A}{1+AH}&=&\frac {-A}{1+g_{m}R_{f}} \\[ 5pt ] \frac {1}{1+AH}&=& \frac {1}{1+g_{m}R_{f}} \\[ 5pt ] AH&=& g_{m}R_{f}　　　　・・・・・・・・・・・・　① \\[ 5pt ] H&=& \frac {g_{m}R_{f}}{A} \\[ 5pt ] &=& \frac {g_{m}R_{f}}{g_{m}R_{L}} \\[ 5pt ] &=& \frac {R_{f}}{R_{L}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヨ
(2)解答式より，
\[
\begin{eqnarray}
i_{in}&=&\frac {v_{in}-v_{e}}{R_{i}} \\[ 5pt ] \end{eqnarray}
\] であり，これに(3)解答式を代入すれば，
\[
\begin{eqnarray}
i_{in}&=&\frac {\displaystyle v_{in}-\frac {g_{m}R_{f}}{1+g_{m}R_{f}}v_{in}}{R_{i}} \\[ 5pt ] &=&\frac {\displaystyle \frac {1+g_{m}R_{f}-g_{m}R_{f}}{1+g_{m}R_{f}}v_{in}}{R_{i}} \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{1+g_{m}R_{f}}v_{in}}{R_{i}} \\[ 5pt ] &=&\frac {v_{in}}{ R_{i}\left( 1+g_{m}R_{f}\right)} \\[ 5pt ] \frac {v_{in}}{i_{in}}&=& R_{i}\left( 1+g_{m}R_{f}\right) \\[ 5pt ] \end{eqnarray}
\] となる。(4)の①式より，\( \ AH= g_{m}R_{f} \ \)であるから，
\[
\begin{eqnarray}
\frac {v_{in}}{i_{in}}&=& R_{i}\left( 1+AH\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。