【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式を解答群の中から選び,その記号をマークシートに記入しなさい。
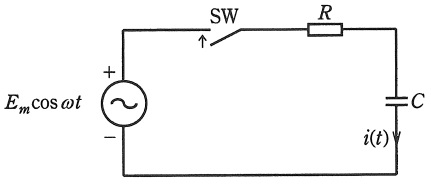
図の回路において,時刻\( \ t=0 \ \)でスイッチ\( \ \mathrm {SW} \ \)を投入した後の電流\( \ i \left( t\right) \ \)をラプラス変換を用いて求めたい。ただし,最大電圧\( \ E_{m} = 100 \ \mathrm {[V]} \ \),静電容量\( \ C=0.001 \ \mathrm {[F]} \ \),抵抗\( \ R=100 \ \mathrm {[\Omega ]} \ \),角周波数\( \ \omega =10 \ \mathrm {[rad / s]} \ \)とし,\( \ C \ \)の初期電荷を\( \ 0 \ \mathrm {[C]} \ \)とする。また,\( \ u \left( t\right) \ \)は単位ステップ関数とする。
この回路を解析するに当たり,計算を簡単化するため交流電源\( \ E_{m}\cos \omega t \ \)を複素交流電源\( \ E_{m}\mathrm {e}^{\mathrm {j}\omega t} \ \)に置き換えて考える。過渡現象を解析するための回路は\( \ t>0 \ \)の状態の回路であるから,スイッチを投入した状態でキルヒホッフの電圧則を適用することにより,回路に流れる複素電流\( \ i^{*} \left( t\right) \ \)に関する方程式\( \ \fbox { (1) } \ \)が得られる。複素電流\( \ i^{*} \left( t\right) \ \)のラプラス変換を\( \ I^{*} \left( s\right) \ \)で表し,式\( \ \fbox { (1) } \ \)の両辺をラプラス変換し,\( \ s \ \)領域の方程式を求めることにより\( \ I^{*} \left( s\right) =\fbox { (2) } \ \)が得られる。さらにこれに各素子と電源に与えられた数値を代入し部分分数に展開すると\( \ I^{*} \left( s\right) =\fbox { (3) } \ \)となる。次に\( \ \fbox { (3) } \ \)をラプラス逆変換することにより\( \ i^{*} \left( t\right) \ \)は\( \ \fbox { (4) } \ \)と求められる。電流\( \ i \left( t\right) \ \)は\( \ i^{*} \left( t\right) \ \)の実部であるから\( \ i \left( t\right) =\fbox { (5) } \ \)となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& E_{m}\mathrm {e}^{\mathrm {j}\omega t}\cdot u \left( t\right) =Ri^{*} \left( t\right) -\frac {1}{C}\int _{0}^{t} i^{*} \left( t^{\prime }\right) \mathrm {d}t^{\prime } &(ロ)& \frac {E_{m}}{R}\cdot \frac {s}{\displaystyle \left( s+\mathrm {j}\omega \right) \left( s-\frac {1}{RC}\right) } \\[ 5pt ]
&(ハ)& \frac {1}{1-\mathrm {j}}\cdot \frac {1}{s-\mathrm {j}10}+\frac {1}{1+\mathrm {j}}\cdot \frac {1}{s+10} &(ニ)& \frac {1}{1+\mathrm {j}}\mathrm {e}^{-\mathrm {j}10t}\cdot u \left( t\right) -\frac {1}{1+\mathrm {j}}\mathrm {e}^{10t}\cdot u \left( t\right) \\[ 5pt ]
&(ホ)& \frac {1}{\sqrt {2}}\cos \left( 10t-\frac {\pi }{4}\right) \cdot u \left( t\right) +\frac {1}{2}\mathrm {e}^{-10t}\cdot u \left( t\right) &(ヘ)& E_{m}\mathrm {e}^{\mathrm {j}\omega t}\cdot u \left( t\right) =Ri^{*} \left( t\right) +\frac {1}{C}\int _{0}^{t} i^{*} \left( t^{\prime }\right) \mathrm {d}t^{\prime } \\[ 5pt ]
&(ト)& \frac {E_{m}}{R}\cdot \frac {s}{\displaystyle \left( s+\mathrm {j}\omega \right) \left( s+\frac {1}{RC}\right) } &(チ)& \frac {1}{1+\mathrm {j}}\cdot \frac {1}{s+\mathrm {j}10}+\frac {1}{1-\mathrm {j}}\cdot \frac {1}{s+10} \\[ 5pt ]
&(リ)& \frac {1}{1-\mathrm {j}}\mathrm {e}^{\mathrm {j}10t}\cdot u \left( t\right) +\frac {1}{1+\mathrm {j}}\mathrm {e}^{-10t}\cdot u \left( t\right) &(ヌ)& \frac {1}{\sqrt {2}}\cos \left( 10t-\frac {\pi }{4}\right) \cdot u \left( t\right) +\frac {1}{2}\mathrm {e}^{10t}\cdot u \left( t\right) \\[ 5pt ]
&(ル)& E_{m}\mathrm {e}^{\mathrm {j}2\omega t}\cdot u \left( t\right) =Ri^{*} \left( t\right) +\frac {1}{C}\int _{0}^{t} i^{*} \left( t^{\prime }\right) \mathrm {d}t^{\prime } &(ヲ)& \frac {E_{m}}{R}\cdot \frac {s}{\displaystyle \left( s-\mathrm {j}\omega \right) \left( s+\frac {1}{RC}\right) } \\[ 5pt ]
&(ワ)& \frac {1}{1-\mathrm {j}}\cdot \frac {1}{s+\mathrm {j}10}+\frac {1}{1+\mathrm {j}}\cdot \frac {1}{s-10} &(カ)& \frac {\mathrm {j}}{1-\mathrm {j}}\mathrm {e}^{\mathrm {j}10t}\cdot u \left( t\right) +\frac {1}{1+\mathrm {j}}\mathrm {e}^{-10t}\cdot u \left( t\right) \\[ 5pt ]
&(ヨ)& \frac {1}{\sqrt {2}}\cos \left( 10t+\frac {\pi }{4}\right) \cdot u \left( t\right) +\frac {1}{2}\mathrm {e}^{-10t}\cdot u \left( t\right) && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
交流電源を接続した\( \ RC \ \)直列回路の過渡現象に関する問題です。
\( \ 2 \ \)種までですと,過渡現象は専ら直流電源を扱いましたが,本問は難易度を上げ交流電源とし,ラプラス変換を使用して解く必要がある問題です。
計算量が多いですが,\( \ 1 \ \)種受験生ですと結構高得点を取得される方が多い問題かと思います。\( \ 2 \ \)種で学習したラプラス変換の知識や部分分数分解の知識を活用して解いていくようにして下さい。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
過渡現象における\( \ RLC \ \)それぞれの電圧は,線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ v_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ v_{\mathrm{L}} \ \),リアクトル\( \ C \ \)の電圧\( \ v_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
v_{\mathrm{R}} &=& Ri \\[ 5pt ]
v_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
v_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\displaystyle \frac {\mathrm {d}f\left( t \right) }{\mathrm {d}t} & sF\left( s \right) -f\left( 0 \right) \\[ 5pt ]
\displaystyle \int f\left( t \right) \mathrm {d}t & \displaystyle \frac {F\left( s \right) }{s}+\frac {1}{s}\int _{-\infty }^{0}f\left( \tau \right) \mathrm {d}\tau \\[ 5pt ]
\hline
\end{array}
\]
3.複素平面における複素数の表記方法
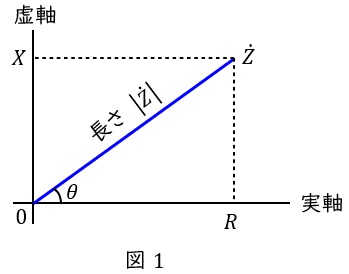
図1のような複素空間上の値\( \ \dot Z =R+\mathrm {j}X \ \)において,以下のような表記方法が定義されます。
ただし,\( \ \dot Z \ \)の絶対値\( \ \left| \dot Z\right| = \sqrt {R^{2}+X^{2}} \ \),\( \ \dot Z \ \)と実軸となす角を\( \ \theta \ \)とします。
①直交座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \left( \cos \theta +\mathrm {j}\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
②指数表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \mathrm {e}^{\mathrm {j}\theta } \\[ 5pt ]
\end{eqnarray}
\]
ただし,
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
であり,これをオイラーの公式といいます。
③極座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| ∠\theta \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ヘ
複素交流電源\( \ E_{m}\mathrm {e}^{\mathrm {j}\omega t} \ \)に置き換えて,スイッチ\( \ \mathrm {SW} \ \)投入後の複素電流\( \ i^{*} \left( t\right) \ \)について回路方程式を立てると,ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電圧」の通り,
\[
\begin{eqnarray}
E_{m}\mathrm {e}^{\mathrm {j}\omega t}&=&Ri^{*} \left( t\right) +\frac {1}{C}\int i^{*} \left( t^{\prime }\right) \mathrm {d}t^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ t=0 \ \)でスイッチ\( \ \mathrm {SW} \ \)を投入したので,
\[
\begin{eqnarray}
E_{m}\mathrm {e}^{\mathrm {j}\omega t}\cdot u \left( t\right) &=&Ri^{*} \left( t\right) +\frac {1}{C}\int _{0}^{t} i^{*} \left( t^{\prime }\right) \mathrm {d}t^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヲ
(1)解答式の両辺をラプラス変換すると,\( \ C \ \)の初期電荷が\( \ 0 \ \mathrm {[C]} \ \)であるから,ワンポイント解説「2.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
\frac {E_{m}}{s-\mathrm {j}\omega }&=&RI^{*} \left( s\right) +\frac {1}{C}\cdot \frac {I^{*} \left( s\right) }{s} \\[ 5pt ]
&=&\left( R+\frac {1}{Cs}\right) I^{*} \left( s\right) \\[ 5pt ]
I^{*} \left( s\right) &=&\frac {E_{m}}{\displaystyle \left( s-\mathrm {j}\omega \right) \left( R+\frac {1}{Cs}\right) } \\[ 5pt ]
&=&\frac {E_{m}}{\displaystyle \frac {R}{s}\left( s-\mathrm {j}\omega \right) \left( s+\frac {1}{RC}\right) } \\[ 5pt ]
&=&\frac {E_{m}}{R}\cdot \frac {s}{\displaystyle \left( s-\mathrm {j}\omega \right) \left( s+\frac {1}{RC}\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ハ
(2)解答式に\( \ E_{m} = 100 \ \mathrm {[V]} \ \),\( \ C=0.001 \ \mathrm {[F]} \ \),\( \ R=100 \ \mathrm {[\Omega ]} \ \),\( \ \omega =10 \ \mathrm {[rad / s]} \ \)を代入すると,
\[
\begin{eqnarray}
I^{*} \left( s\right) &=&\frac {E_{m}}{R}\cdot \frac {s}{\displaystyle \left( s-\mathrm {j}\omega \right) \left( s+\frac {1}{RC}\right) } \\[ 5pt ]
&=&\frac {100}{100}\times \frac {s}{\displaystyle \left( s-\mathrm {j}10 \right) \left( s+\frac {1}{100\times 0.001}\right) } \\[ 5pt ]
&=&\frac {s}{\displaystyle \left( s-\mathrm {j}10 \right) \left( s+10\right) } \\[ 5pt ]
\end{eqnarray}
\]
となり,部分分数分解するために,\( \ \displaystyle I^{*} \left( s\right) =\frac {A}{s-\mathrm {j}10 }+\frac {B}{s+10} \ \)とおき,これを変形すると,
\[
\begin{eqnarray}
I^{*} \left( s\right) &=&\frac {A\left( s+10\right) +B\left( s-\mathrm {j}10 \right) }{\displaystyle \left( s-\mathrm {j}10 \right) \left( s+10\right) } \\[ 5pt ]
&=&\frac {\left( A+B\right) s+10A-\mathrm {j}10B}{\displaystyle \left( s-\mathrm {j}10 \right) \left( s+10\right) } \\[ 5pt ]
\end{eqnarray}
\]
となる。両者を係数比較すれば,
\[
\begin{eqnarray}
\left\{
\begin{array}{r}
A &+& B &=& 1 & ・・・・・・・・・・ ① & \\[ 5pt ]
10A&-&\mathrm {j}10B &=& 0 & ・・・・・・・・・・ ② & \\[ 5pt ]
\end{array}
\right.
\end{eqnarray}
\]
と連立方程式が立てられる。②より\( \ A=\mathrm {j}B \ \)となるので,これを①に代入すると,
\[
\begin{eqnarray}
\mathrm {j}B+B &=&1 \\[ 5pt ]
\left( 1+\mathrm {j}\right) B&=&1 \\[ 5pt ]
B&=&\frac {1}{1+\mathrm {j}} \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
A &=&\mathrm {j}B \\[ 5pt ]
&=&\frac {\mathrm {j}}{1+\mathrm {j}} \\[ 5pt ]
&=&\frac {1}{\displaystyle \frac {1}{\mathrm {j}}\left( 1+\mathrm {j}\right) } \\[ 5pt ]
&=&\frac {1}{-\mathrm {j}\left( 1+\mathrm {j}\right) } \left( ∵\frac {1}{\mathrm {j}}=\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}}=-\mathrm {j}\right) \\[ 5pt ]
&=&\frac {1}{1-\mathrm {j}} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,\( \ I^{*} \left( s\right) \ \)は,
\[
\begin{eqnarray}
I^{*} \left( s\right) &=&\frac {A}{s-\mathrm {j}10 }+\frac {B}{s+10} \\[ 5pt ]
&=&\frac {\displaystyle \frac {1}{1-\mathrm {j}}}{s-\mathrm {j}10 }+\frac {\displaystyle \frac {1}{1+\mathrm {j}}}{s+10} \\[ 5pt ]
&=&\frac {1}{1-\mathrm {j}}\cdot \frac {1}{s-\mathrm {j}10}+\frac {1}{1+\mathrm {j}}\cdot \frac {1}{s+10} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:リ
(3)解答式をラプラス逆変換すると,ワンポイント解説「2.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
i^{*} \left( t\right) &=&\frac {1}{1-\mathrm {j}}\mathrm {e}^{\mathrm {j}10t}\cdot u \left( t\right) +\frac {1}{1+\mathrm {j}}\mathrm {e}^{-10t}\cdot u \left( t\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヨ
(4)解答式において,\( \ \displaystyle \frac {1}{1-\mathrm {j}} \ \)及び\( \ \displaystyle \frac {1}{1+\mathrm {j}} \ \)を指数関数表記に変換すると,ワンポイント解説「3.複素平面における複素数の表記方法」の通り,
\[
\begin{eqnarray}
\frac {1}{1-\mathrm {j}} &=&\frac {1}{\sqrt {1^{2}+1^{2}}\mathrm {e}^{-\mathrm {j}\frac {\pi }{4}}} \\[ 5pt ]
&=&\frac {1}{\sqrt {2}}\mathrm {e}^{\mathrm {j}\frac {\pi }{4}} \\[ 5pt ]
\frac {1}{1+\mathrm {j}} &=&\frac {1}{\sqrt {1^{2}+1^{2}}\mathrm {e}^{\mathrm {j}\frac {\pi }{4}}} \\[ 5pt ]
&=&\frac {1}{\sqrt {2}}\mathrm {e}^{-\mathrm {j}\frac {\pi }{4}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,(4)解答式は,
\[
\begin{eqnarray}
i^{*} \left( t\right) &=&\frac {1}{\sqrt {2}}\mathrm {e}^{\mathrm {j}\frac {\pi }{4}}\mathrm {e}^{\mathrm {j}10t}\cdot u \left( t\right) +\frac {1}{\sqrt {2}}\mathrm {e}^{-\mathrm {j}\frac {\pi }{4}}\mathrm {e}^{-10t}\cdot u \left( t\right) \\[ 5pt ]
&=&\frac {1}{\sqrt {2}}\mathrm {e}^{\mathrm {j}\left( 10t+\frac {\pi }{4}\right) }\cdot u \left( t\right) +\frac {1}{\sqrt {2}}\mathrm {e}^{-\mathrm {j}\frac {\pi }{4}}\mathrm {e}^{-10t}\cdot u \left( t\right) \\[ 5pt ]
&=&\frac {1}{\sqrt {2}}\left\{ \cos \left( 10t+\frac {\pi }{4}\right) +\mathrm {j}\sin \left( 10t+\frac {\pi }{4}\right) \right\} \cdot u \left( t\right) +\frac {1}{\sqrt {2}}\left\{ \cos \left( -\frac {\pi }{4}\right) +\mathrm {j}\sin \left( -\frac {\pi }{4}\right) \right\} \mathrm {e}^{-10t}\cdot u \left( t\right) \\[ 5pt ]
\end{eqnarray}
\]
と変形できる。題意より,\( \ i \left( t\right) \ \)は\( \ i^{*} \left( t\right) \ \)の実部であるから,
\[
\begin{eqnarray}
i \left( t\right) &=&\frac {1}{\sqrt {2}}\cos \left( 10t+\frac {\pi }{4}\right) \cdot u \left( t\right) +\frac {1}{\sqrt {2}}\cos \left( -\frac {\pi }{4}\right) \mathrm {e}^{-10t}\cdot u \left( t\right) \\[ 5pt ]
&=&\frac {1}{\sqrt {2}}\cos \left( 10t+\frac {\pi }{4}\right) \cdot u \left( t\right) +\frac {1}{\sqrt {2}}\cdot \frac {1}{\sqrt {2}} \mathrm {e}^{-10t}\cdot u \left( t\right) \\[ 5pt ]
&=&\frac {1}{\sqrt {2}}\cos \left( 10t+\frac {\pi }{4}\right) \cdot u \left( t\right) +\frac {1}{2}\mathrm {e}^{-10t}\cdot u \left( t\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん