【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,三相交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
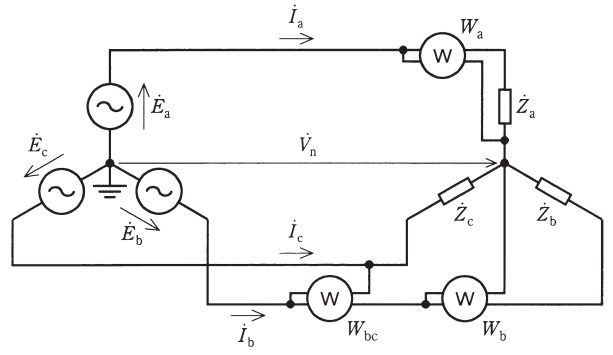
図に示すように,対称三相交流電源に\( \ \mathrm {Y} \ \)形不平衡負荷及び\( \ 3 \ \)個の電力計を接続した。\( \ {\dot E}_{\mathrm {a}}=100∠0° \ \mathrm {[V]} \ \)であり,相回転は\( \ {\dot E}_{\mathrm {a}} \ \),\( \ {\dot E}_{\mathrm {b}} \ \),\( \ {\dot E}_{\mathrm {c}} \ \)の順とする。このとき線電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \)はそれぞれ\( \ {\dot E}_{\mathrm {a}} \ \),\( \ {\dot E}_{\mathrm {b}} \ \)と同相となり,\( \ {\dot I}_{\mathrm {a}}=5∠0° \ \mathrm {[A]} \ \)であった。また,電力計の値は\( \ W_{\mathrm {a}}=250 \ \mathrm {[W]} \ \),\( \ W_{\mathrm {b}}=500 \ \mathrm {[W]} \ \),\( \ W_{\mathrm {bc}}=1 \ 500 \ \mathrm {[W]} \ \)であった。\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi }{3}} \ \)とおくと,線電流\( \ {\dot I}_{\mathrm {b}} \ \)の条件から,\( \ {\dot I}_{\mathrm {b}}=\left| {\dot I}_{\mathrm {b}} \right| \times \ \fbox { (1) } \ \)である。
\( \ W_{\mathrm {bc}}=\mathrm {Re} \left[ \left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}\right) \overline {{\dot I}_{\mathrm {b}}}\right] \ \)及び\( \ a^{3}=1 \ \)を利用すると,\( \ {\dot I}_{\mathrm {b}}= \ \fbox { (2) } \ \mathrm {[A]} \ \)となり,\( \ {\dot I}_{\mathrm {c}} \ \)も\( \ {\dot I}_{\mathrm {a}} \ \)と\( \ {\dot I}_{\mathrm {b}} \ \)から計算できる。このとき,各負荷の消費電力の総和は\( \ \mathrm {Re} \left[ \left( {\dot E}_{\mathrm {a}}-{\dot V}_{\mathrm {n}}\right) \overline {{\dot I}_{\mathrm {a}}}+\left( {\dot E}_{\mathrm {b}}-{\dot V}_{\mathrm {n}}\right) \overline {{\dot I}_{\mathrm {b}}}+\left( {\dot E}_{\mathrm {c}}-{\dot V}_{\mathrm {n}}\right) \overline {{\dot I}_{\mathrm {c}}}\right] =\mathrm {Re} \left[ \left( \fbox { (3) }\right) \overline {{\dot I}_{\mathrm {a}}}\right] +W_{\mathrm {bc}} \ \)となる。この式の右辺第一項の複素数の計算を行うと,\( \ W_{\mathrm {bc}}=1 \ 500 \ \mathrm {[W]} \ \)であるから,\( \ \mathrm {Y} \ \)形負荷全体の消費電力は\( \ \fbox { (4) } \ \mathrm {[W]} \ \)と求められる。
以上のことから,各負荷の消費電力と電流の大きさを考えることにより,各負荷の抵抗成分の総和\( \ \mathrm {Re} \left[ {\dot Z}_{\mathrm {a}}\right] +\mathrm {Re} \left[ {\dot Z}_{\mathrm {b}}\right] +\mathrm {Re} \left[ {\dot Z}_{\mathrm {c}}\right] \ \)は\( \ \fbox { (5) } \ \mathrm {[\Omega ]} \ \)と求まる。
(注)\( \ \mathrm {Re} \left[ \dot Z\right] \ \)は複素数\( \ \dot Z \ \)の実部を表す。
\( \ \overline {\dot Z} \ \)は複素数\( \ \dot Z \ \)の共役複素数を表す。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& 50a &(ロ)& 35 &(ハ)& 2 \ 200 \\[ 5pt ]
&(ニ)& 20a &(ホ)& {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}} &(ヘ)& 2 \ 000 \\[ 5pt ]
&(ト)& {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {c}} &(チ)& 1 &(リ)& 2 \ 250 \\[ 5pt ]
&(ヌ)& 40 &(ル)& a^{2} &(ヲ)& {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}} \\[ 5pt ]
&(ワ)& 10a^{2} &(カ)& 50 &(ヨ)& a \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三相不平衡負荷における消費電力に関する問題です。
\( \ \Delta – \mathrm {Y} \ \)変換や\( \ \mathrm {Y} – \Delta \ \)変換を使用した問題が多い電験\( \ 1 \ \)種の問\( \ 5 \ \)ですが,この年は使用しない代わりにやや計算量の多い問題が出題されました。
例年の問\( \ 5 \ \)にしては比較的取り組みやすい問題かなとも思いますので,\( \ 3 \ \)つの小問程度は確実に得点できるようになりましょう。
1.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータ\( \ a \ \)は,\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ]
&=& 1 \\[ 5pt ]
\end{eqnarray}
\]
となります。上記より,
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ]
1+a+a^{2}&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかります。
【解答】
(1)解答:ル
題意より,線電流\( \ {\dot I}_{\mathrm {b}} \ \)は\( \ {\dot E}_{\mathrm {b}} \ \)と同相であり,\( \ {\dot E}_{\mathrm {b}}=100a^{2} \ \)であるから,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {b}}&=&\left| {\dot I}_{\mathrm {b}} \right| \times a^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ワ
\( \ W_{\mathrm {bc}}=\mathrm {Re} \left[ \left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}\right) \overline {{\dot I}_{\mathrm {b}}}\right] \ \)であり,ワンポイント解説「1.ベクトルオペレータ\( \ a \ \)」の通り\( \ \overline {{\dot I}_{\mathrm {b}}}=\overline {\left| {\dot I}_{\mathrm {b}} \right| a^{2}}=\left| {\dot I}_{\mathrm {b}} \right| a \ \)であるから,
\[
\begin{eqnarray}
W_{\mathrm {bc}}&=&\mathrm {Re} \left[ \left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}\right) \overline {{\dot I}_{\mathrm {b}}}\right] \\[ 5pt ]
&=&\mathrm {Re} \left[ \left( 100a^{2}-100a\right) \left| {\dot I}_{\mathrm {b}} \right| a\right] \\[ 5pt ]
&=&\mathrm {Re} \left[ \left( 100a^{3}-100a^{2}\right) \left| {\dot I}_{\mathrm {b}} \right| \right] \\[ 5pt ]
&=&\mathrm {Re} \left[ \left( 100-100a^{2}\right) \left| {\dot I}_{\mathrm {b}} \right| \right] \\[ 5pt ]
&=&\mathrm {Re} \left[ 100\left( 1-a^{2}\right) \left| {\dot I}_{\mathrm {b}} \right| \right] \\[ 5pt ]
&=&\mathrm {Re} \left[ 100\left\{ 1-\left( -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2}\right) \right\} \left| {\dot I}_{\mathrm {b}} \right| \right] \\[ 5pt ]
&=&\mathrm {Re} \left[ 100\left( \frac {3}{2}+\mathrm {j}\frac {\sqrt {3}}{2}\right) \left| {\dot I}_{\mathrm {b}} \right| \right] \\[ 5pt ]
&=&\mathrm {Re} \left[ \left( 150+\mathrm {j}50\sqrt {3}\right) \left| {\dot I}_{\mathrm {b}} \right| \right] \\[ 5pt ]
&=&150 \left| {\dot I}_{\mathrm {b}} \right| \\[ 5pt ]
\left| {\dot I}_{\mathrm {b}} \right| &=&\frac {1500}{150} \\[ 5pt ]
&=&10 \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {b}}&=&\left| {\dot I}_{\mathrm {b}} \right| \times a^{2} \\[ 5pt ]
&=&10 a^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ト
(2)及び\( \ {\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}}=0 \ \)から\( \ {\dot I}_{\mathrm {c}} \ \)を求めると,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {c}}&=&-{\dot I}_{\mathrm {a}}-{\dot I}_{\mathrm {b}} \\[ 5pt ]
&=&-5-10 a^{2} \\[ 5pt ]
&=&-5-10\left( -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \right) \\[ 5pt ]
&=&\mathrm {j}5\sqrt {3} \\[ 5pt ]
\end{eqnarray}
\]
となる。与えられている各負荷の消費電力の総和の式を整理すると,
\[
\begin{eqnarray}
\mathrm {Re} \left[ \left( {\dot E}_{\mathrm {a}}-{\dot V}_{\mathrm {n}}\right) \overline {{\dot I}_{\mathrm {a}}}+\left( {\dot E}_{\mathrm {b}}-{\dot V}_{\mathrm {n}}\right) \overline {{\dot I}_{\mathrm {b}}}+\left( {\dot E}_{\mathrm {c}}-{\dot V}_{\mathrm {n}}\right) \overline {{\dot I}_{\mathrm {c}}}\right] &=&\mathrm {Re} \left[ {\dot E}_{\mathrm {a}}\overline {{\dot I}_{\mathrm {a}}}-{\dot V}_{\mathrm {n}}\overline {{\dot I}_{\mathrm {a}}}+{\dot E}_{\mathrm {b}}\overline {{\dot I}_{\mathrm {b}}}-{\dot V}_{\mathrm {n}}\overline {{\dot I}_{\mathrm {b}}}+{\dot E}_{\mathrm {c}}\overline {{\dot I}_{\mathrm {c}}}-{\dot V}_{\mathrm {n}}\overline {{\dot I}_{\mathrm {c}}} \right] \\[ 5pt ]
&=&\mathrm {Re} \left[ {\dot E}_{\mathrm {a}}\overline {{\dot I}_{\mathrm {a}}}+{\dot E}_{\mathrm {b}}\overline {{\dot I}_{\mathrm {b}}}+{\dot E}_{\mathrm {c}}\overline {{\dot I}_{\mathrm {c}}}-{\dot V}_{\mathrm {n}}\overline {{\dot I}_{\mathrm {a}}}-{\dot V}_{\mathrm {n}}\overline {{\dot I}_{\mathrm {b}}}-{\dot V}_{\mathrm {n}}\overline {{\dot I}_{\mathrm {c}}} \right] \\[ 5pt ]
&=&\mathrm {Re} \left[ {\dot E}_{\mathrm {a}}\overline {{\dot I}_{\mathrm {a}}}+{\dot E}_{\mathrm {b}}\overline {{\dot I}_{\mathrm {b}}}+{\dot E}_{\mathrm {c}}\overline {{\dot I}_{\mathrm {c}}}-{\dot V}_{\mathrm {n}}\left( \overline {{\dot I}_{\mathrm {a}}}+\overline {{\dot I}_{\mathrm {b}}}+\overline {{\dot I}_{\mathrm {c}}}\right) \right] \\[ 5pt ]
&=&\mathrm {Re} \left[ {\dot E}_{\mathrm {a}}\overline {{\dot I}_{\mathrm {a}}}+{\dot E}_{\mathrm {b}}\overline {{\dot I}_{\mathrm {b}}}+{\dot E}_{\mathrm {c}}\overline {{\dot I}_{\mathrm {c}}}\right] \left( ∵\overline {{\dot I}_{\mathrm {a}}}+\overline {{\dot I}_{\mathrm {b}}}+\overline {{\dot I}_{\mathrm {c}}}=0\right) \\[ 5pt ]
&=&\mathrm {Re} \left[ {\dot E}_{\mathrm {a}}\overline {{\dot I}_{\mathrm {a}}}+{\dot E}_{\mathrm {b}}\overline {{\dot I}_{\mathrm {b}}}+{\dot E}_{\mathrm {c}}\left( -\overline {{\dot I}_{\mathrm {a}}}-\overline {{\dot I}_{\mathrm {b}}}\right) \right] \\[ 5pt ]
&=&\mathrm {Re} \left[ \left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {c}}\right) \overline {{\dot I}_{\mathrm {a}}}+\left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}\right) \overline {{\dot I}_{\mathrm {b}}} \right] \\[ 5pt ]
&=&\mathrm {Re} \left[ \left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {c}}\right) \overline {{\dot I}_{\mathrm {a}}} \right] +W_{\mathrm {bc}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:リ
(3)の解答式に各値を代入すると,
\[
\begin{eqnarray}
\mathrm {Re} \left[ \left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {c}}\right) \overline {{\dot I}_{\mathrm {a}}} \right] +W_{\mathrm {bc}}&=&\mathrm {Re} \left[ \left( 100-100a\right) \times 5 \right] +1500 \\[ 5pt ]
&=&\mathrm {Re} \left[ 500\left( 1-a\right) \right] +1500 \\[ 5pt ]
&=&\mathrm {Re} \left[ 500\left\{ 1-\left( -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \right) \right\} \right] +1500 \\[ 5pt ]
&=&\mathrm {Re} \left[ 500\left( \frac {3}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \right) \right] +1500 \\[ 5pt ]
&=&\mathrm {Re} \left[ 750-\mathrm {j}250\sqrt {3} \right] +1500 \\[ 5pt ]
&=&750 +1500 \\[ 5pt ]
&=&2250 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ロ
負荷\( \ {\dot Z}_{\mathrm {c}} \ \)での消費電力\( \ W_{\mathrm {c}} \ \)は,消費電力の総和が\( \ 2250 \ \mathrm {W} \ \)であるから,
\[
\begin{eqnarray}
W_{\mathrm {a}}+W_{\mathrm {b}}+W_{\mathrm {c}}&=&2250 \\[ 5pt ]
W_{\mathrm {c}}&=&2250-W_{\mathrm {a}}-W_{\mathrm {b}} \\[ 5pt ]
&=&2250-250-500 \\[ 5pt ]
&=&1500 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,各負荷の抵抗成分の総和\( \ \mathrm {Re} \left[ {\dot Z}_{\mathrm {a}}\right] +\mathrm {Re} \left[ {\dot Z}_{\mathrm {b}}\right] +\mathrm {Re} \left[ {\dot Z}_{\mathrm {c}}\right] \ \)は,
\[
\begin{eqnarray}
\mathrm {Re} \left[ {\dot Z}_{\mathrm {a}}\right] +\mathrm {Re} \left[ {\dot Z}_{\mathrm {b}}\right] +\mathrm {Re} \left[ {\dot Z}_{\mathrm {c}}\right]&=&\frac {W_{\mathrm {a}}}{\left| I_{\mathrm {a}}\right| ^{2} }+\frac {W_{\mathrm {b}}}{\left| I_{\mathrm {b}}\right| ^{2} }+\frac {W_{\mathrm {c}}}{\left| I_{\mathrm {c}}\right| ^{2} } \\[ 5pt ]
&=&\frac {250}{5 ^{2} }+\frac {500}{10^{2} }+\frac {1500}{\left( 5\sqrt {3}\right) ^{2} } \\[ 5pt ]
&=&10+5+20 \\[ 5pt ]
&=&35 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん