《理論》〈電気回路〉[H28:問5] 三相交流回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，三相交流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。ただし，$ \ \displaystyle a=\mathrm {e}^{\mathrm {j}\frac {2}{3}\pi } \ $であり，$ \ 1+a+a^{2}=0 \ $に注意する。

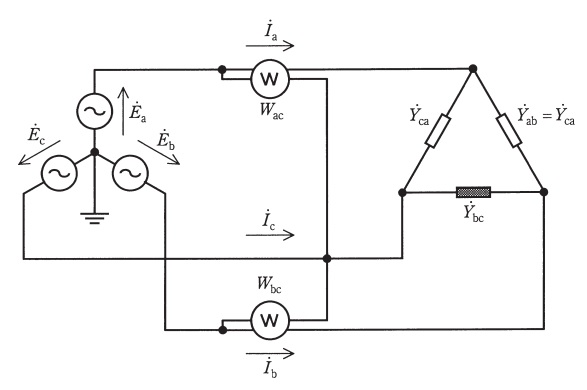
図に示すように，対称三相交流電圧源に$ \ \mathrm {\Delta } \ $形不平衡負荷を接続し，単相電力計を2か所に接続した。$ \ {\dot E}_{\mathrm {a}}=100∠0°\mathrm {V} \ $であり，相回転は$ \ {\dot E}_{\mathrm {a}} \ $，$ \ {\dot E}_{\mathrm {b}} \ $，$ \ {\dot E}_{\mathrm {c}} \ $の順($ \ {\dot E}_{\mathrm {b}}=a^{2}{\dot E}_{\mathrm {a}} \ $，$ \ {\dot E}_{\mathrm {c}}=a{\dot E}_{\mathrm {a}} \ $)とする。$ \ \mathrm {\Delta } \ $形不平衡負荷のアドミタンスは$ \ {\dot Y}_{\mathrm {ab}}={\dot Y}_{\mathrm {ca}} \ $であり，アドミタンス$ \ {\dot Y}_{\mathrm {bc}} \ $は取り外し可能となっている。単相電力計の動作は理想的とし，その接続の仕方は指示が逆振れしない接続とする。このとき，以下の(a)，(b)，(c)の結果を得た。

(a)　アドミタンス$ \ {\dot Y}_{\mathrm {bc}} \ $を除去したとき，線電流$ \ {\dot I}_{\mathrm {a}} \ $は$ \ {\dot I}_{\mathrm {a}}=-3a \left[ \mathrm {A} \right] \ $であった。
(b)　アドミタンス$ \ {\dot Y}_{\mathrm {bc}} \ $を接続したとき，線電流$ \ {\dot I}_{\mathrm {b}} \ $は$ \ {\dot I}_{\mathrm {b}}=a \left[ \mathrm {A} \right] \ $であった。
(c)　単相電力計の指示$ \ {W}_{\mathrm {ac}} \ $と$ \ {W}_{\mathrm {bc}} \ $のそれぞれの値は，(a)と(b)で同じであった。

ただし，単相電力計の接続の仕方は，指示値$ \ {W}_{\mathrm {ac}} \ $を読むときと指示値$ \ {W}_{\mathrm {bc}} \ $を読むときでは，極性が逆となった。

(a)のとき，$ \ {\dot Y}_{\mathrm {ab}}={\dot Y}_{\mathrm {ca}} \ $及び$ \ {\dot I}_{\mathrm {a}}=\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}\right) {\dot Y}_{\mathrm {ab}}+\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {c}}\right) {\dot Y}_{\mathrm {ca}} \ $に注意すると，$ \ {\dot Y}_{\mathrm {ab}}={\dot Y}_{\mathrm {ca}}= \ \fbox {　（１）　} \ \left [ \mathrm {S} \right] \ $となる。図の三相回路の線電流$ \ {\dot I}_{\mathrm {a}} \ $の値は$ \ {\dot Y}_{\mathrm {bc}} \ $と無関係であるから，単相電力計の指示値$ \ {W}_{\mathrm {ac}} \ $は(a)でも(b)でも$ \ {W}_{\mathrm {ac}}= \ \fbox {　（２）　} \ \mathrm {W} \ $を示す。

$ \ {\dot Y}_{\mathrm {bc}} \ $を除去することは，$ \ {\dot Y}_{\mathrm {bc}}=0 \ \mathrm {S} \ $とすることと等価であるから，(a)のときの線電流$ \ {\dot I}_{\mathrm {b}} \ $は，$ \ {\dot I}_{\mathrm {b}}=\left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {a}}\right) {\dot Y}_{\mathrm {ab}} \ $より，$ \ {\dot I}_{\mathrm {b}}= \ \fbox {　（３）　} \ \left [ \mathrm {A} \right] \ $となる。(c)の結果からアドミタンス$ \ {\dot Y}_{\mathrm {bc}} \ $は電力を消費しないことが分かる。したがって，図の$ \ \mathrm {\Delta } \ $形不平衡負荷の消費電力は$ \ {\dot Y}_{\mathrm {ab}} \ $と$ \ {\dot Y}_{\mathrm {ca}} \ $から求めることができ，(a)でも(b)でも$ \ \fbox {　（４）　} \ \mathrm {W} \ $を得る。以上の結果と$ \ {W}_{\mathrm {ac}} \ $の値の大きさに注意すると，$ \ {W}_{\mathrm {bc}} \ $が指示するのは負荷から電源に戻る回生電力の値であることが分かる。したがって，(a)でも(b)でも$ \ {W}_{\mathrm {bc}}= \ \fbox {　（５）　} \ \mathrm {W} \ $を得る。$ \ {W}_{\mathrm {bc}} \ $の値は(a)又は(b)のときの線電流$ \ {\dot I}_{\mathrm {b}} \ $から求めることもできる。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　300　　　　　&（ロ）&　\sqrt {3} a^{2}　　　　&（ハ）&　150　 \\[ 5pt ] &（ニ）&　0.01　　　　　&（ホ）&　\sqrt {3} \left( a^{2}-1\right)　　　　&（ヘ）&　a-1 \\[ 5pt ] &（ト）&　600　　　　　&（チ）&　750　　　&（リ）&　200 \\[ 5pt ] &（ヌ）&　-0.01a^{2}　　　　　&（ル）&　450　　　&（ヲ）&　100 \\[ 5pt ] &（ワ）&　400　　　　　&（カ）&　-0.01a　　　&（ヨ）&　250
\end{eqnarray}
\]

【ワンポイント解説】

本問は落ち着いて問題文を読み，計算式を解けば，それほど難しい問題ではありません。交流回路の消費電力の公式とベクトルオペレータについては毎年のように出題されるので，よく理解しておくようにしておきましょう。

1.交流回路の消費電力$ \ W \ $
ある回路に電圧$ \ \dot {E} \ $，電流$ \ \dot {I} \ $で交流電流が流れているとき，消費電力$ \ W \ $は遅れ無効電力を正とすると，
\[
W=\mathrm {Re} \left[ \ \dot {E} \ \overline {\dot {I}} \ \right] \] で求められます。

2.ベクトルオペレータ$ \ a \ $
題意で与えられているベクトルオペレータ$ \ a=\mathrm{e}^{\mathrm{j}\frac {2\pi}{3}} \ $は，
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm{j}\sin \frac {2\pi}{3} &=& -\frac {1}{2}+\mathrm{j}\frac {\sqrt {3}}{2} \\[ 5pt ] a^{2} &=& \cos \frac {4\pi}{3}+\mathrm{j}\sin \frac {4\pi}{3} &=& -\frac {1}{2}-\mathrm{j}\frac {\sqrt {3}}{2} \\[ 5pt ] a^{3} &=& \cos \frac {6\pi}{3}+\mathrm{j}\sin \frac {6\pi}{3} &=& 1
\end{eqnarray}
\] となります。したがって，
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ] \overline {a^{2}} &=& a \\[ 5pt ] 1+a+a^{2} &=& 0
\end{eqnarray}
\] が成立します。

【解答】

(1)解答：カ
$ \ {\dot Y}_{\mathrm {ab}}={\dot Y}_{\mathrm {ca}} \ $及び$ \ {\dot I}_{\mathrm {a}}=\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}\right) {\dot Y}_{\mathrm {ab}}+\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {c}}\right) {\dot Y}_{\mathrm {ca}} \ $より，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}}&=&\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}\right) {\dot Y}_{\mathrm {ab}}+\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {c}}\right) {\dot Y}_{\mathrm {ca}} \\[ 5pt ] {\dot I}_{\mathrm {a}}&=&\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}\right) {\dot Y}_{\mathrm {ab}}+\left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {c}}\right) {\dot Y}_{\mathrm {ab}} \\[ 5pt ] {\dot I}_{\mathrm {a}}&=&\left( 2{\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}\right) {\dot Y}_{\mathrm {ab}} \\[ 5pt ] {\dot Y}_{\mathrm {ab}}&=&\frac {{\dot I}_{\mathrm {a}}}{2{\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}}
\end{eqnarray}
\] であるから，$ \ {\dot I}_{\mathrm {a}}=-3a \ $，$ \ {\dot E}_{\mathrm {a}}=100 \ $，$ \ {\dot E}_{\mathrm {b}}=100a^{2} \ $，$ \ {\dot E}_{\mathrm {c}}=100a \ $を代入すると，
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {ab}}&=&\frac {-3a}{2\cdot 100-100a^{2}-100a} \\[ 5pt ] &=&\frac {-3a}{200-100\left( a^{2}+a\right) } \\[ 5pt ] &=&\frac {-3a}{200-100\cdot \left( -1\right) } \\[ 5pt ] &=&\frac {-3a}{300 } \\[ 5pt ] &=&-0.01a \ \left [ \mathrm {S} \right] \end{eqnarray}
\] と求められる。

(2)解答：ル
ワンポイント解説「1.交流回路の消費電力$ \ W \ $」より，
\[
\begin{eqnarray}
W_{\mathrm {ac}}&=&\mathrm {Re} \left[ \ \left( {\dot E}_{\mathrm {a}}-{\dot E}_{\mathrm {c}}\right) \ \overline {{\dot I}_{\mathrm {a}}} \ \right] \\[ 5pt ] &=&\mathrm {Re} \left[ \ \left( 100-100a\right) \cdot \overline {-3a} \ \right] \\[ 5pt ] &=&\mathrm {Re} \left[ \ 100\left( 1-a\right) \cdot \left( -3a^{2} \right) \right] \\[ 5pt ] &=&\mathrm {Re} \left[ \ 300\left( 1-a^{2}\right) \right] \\[ 5pt ] &=&\mathrm {Re} \left[ 450+\mathrm{j}150\sqrt {3} \right] \\[ 5pt ] &=&450 \ \left[ \mathrm {W}\right] \end{eqnarray}
\] と求められる。

(3)解答：ヘ
題意より，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {b}}&=&\left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {a}}\right) {\dot Y}_{\mathrm {ab}} \\[ 5pt ] &=&\left( 100a^{2}-100\right) \left( -0.01a\right) \\[ 5pt ] &=&a-1 \ \left[ \mathrm {A} \right] \end{eqnarray}
\] と求められる。

(4)解答：イ
$ \ {\dot Y}_{\mathrm {ab}}={\dot Y}_{\mathrm {ca}} \ $であり，どちらも同電圧がかかっているので，消費電力が等しい。したがって，負荷全体の消費電力は$ \ {\dot Y}_{\mathrm {ab}} \ $の2倍となる。よって，負荷全体の消費電力$ \ W \ $は
\[
\begin{eqnarray}
W&=&2\mathrm {Re} \left[ \ \left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {a}}\right) \ \overline {{\dot I}_{\mathrm {b}}} \ \right] \\[ 5pt ] &=&2\mathrm {Re} \left[ \ \left( 100a^{2}-100\right) \cdot \overline {a-1} \ \right] \\[ 5pt ] &=&2\mathrm {Re} \left[ \ 100\left( a^{2}-1\right) \left( a^{2}-1 \right) \right] \\[ 5pt ] &=&2\mathrm {Re} \left[ \ 100\left( a-2a^{2}+1\right) \right] \\[ 5pt ] &=&2\mathrm {Re} \left[ \ 100\left( 3+3a\right) \right] \\[ 5pt ] &=&2\mathrm {Re} \left[ \ 150+\mathrm{j}150\sqrt {3} \right] \\[ 5pt ] &=&300 \ \left[ \mathrm {W}\right] \end{eqnarray}
\] と求められる。

(5)解答：ハ
$ \ {W}_{\mathrm {bc}} \ $が指示する電力は，
\[
\begin{eqnarray}
W_{\mathrm {bc}}&=&\mathrm {Re} \left[ \ \left( {\dot E}_{\mathrm {b}}-{\dot E}_{\mathrm {c}}\right) \ \overline {{\dot I}_{\mathrm {b}}} \ \right] \\[ 5pt ] &=&\mathrm {Re} \left[ \ \left( 100a^{2}-100a\right) \cdot \overline {a-1} \ \right] \\[ 5pt ] &=&\mathrm {Re} \left[ \ 100\left( a^{2}-a\right) \cdot \left( a^{2}-1 \right) \right] \\[ 5pt ] &=&\mathrm {Re} \left[ \ 100\left( a^{4}-a^{3}-a^{2}+a\right) \right] \\[ 5pt ] &=&\mathrm {Re} \left[ \ 100\left( -1+2a-a^{2}\right) \right] \\[ 5pt ] &=&\mathrm {Re} \left[ 300a \right] \\[ 5pt ] &=&\mathrm {Re} \left[ -150+\mathrm{j}150\sqrt {3} \right] \\[ 5pt ] &=&-150 \left[ \mathrm {W}\right] \end{eqnarray}
\] となる。問題文にて，「単相電力計の動作は理想的とし，その接続の仕方は指示が逆振れしない接続とする。」となっているので，解答は$ \ 150\left[ \mathrm {W}\right] \ $となる。