【問題】
【難易度】★★★☆☆(普通)
次の文章は,三相交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
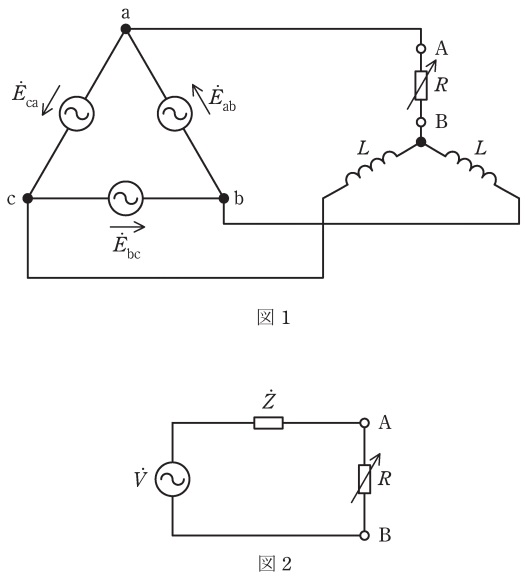
図1のように,インダクタ\( \ L \ \)と可変抵抗\( \ R \ \)から構成される\( \ \mathrm {Y} \ \)形不平衡負荷に対称三相交流電源が接続されている。線間電圧の大きさは\( \ \left| {\dot E}_{\mathrm {ab}} \right| =\left| {\dot E}_{\mathrm {bc}} \right| =\left| {\dot E}_{\mathrm {ca}} \right| =E \ \),電源の角周波数は\( \ \omega \ \)である。
図1において,端子\( \ \mathrm {A-B} \ \)から見たテブナンの等価回路を考えれば,図2の等価回路が得られる。図2の等価回路において,インピーダンス\( \ {\dot Z}= \ \fbox { (1) } \ \)であり,電源の電圧の大きさ\( \ \left| \dot V \right| = \ \fbox { (2) } \ \)である。
図2において,可変抵抗\( \ R \ \)を流れる電流\( \ {\dot I}_{\mathrm {R}} \ \)の大きさ\( \ \left| {\dot I}_{\mathrm {R}} \right| = \ \fbox { (3) } \ \)となる。可変抵抗\( \ R \ \)で消費される有効電力\( \ P_{\mathrm {R}} = \ \fbox { (4) } \ \)であり,\( \ \fbox { (5) } \ \)の条件が成立するとき,\( \ P_{\mathrm {R}} \ \)は最大となる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& \mathrm {j}2\omega L &(ロ)& \frac {\displaystyle \frac {E}{\sqrt {3}}}{\sqrt {R^{2}+\left( \omega L \right) ^{2} }} &(ハ)& \frac {\displaystyle \frac {E}{2}}{\sqrt {R^{2}+\left( 2\omega L \right) ^{2} }} \\[ 5pt ]
&(ニ)& R=2\omega L &(ホ)& \frac {E}{2} &(ヘ)& \frac {\displaystyle \frac {\sqrt {3}E}{2}}{\sqrt {R^{2}+\left( \displaystyle \frac {\omega L}{2} \right) ^{2} }} \\[ 5pt ]
&(ト)& \frac {\displaystyle \frac {RE^{2}}{3}}{R^{2}+\left( \omega L \right) ^{2} } &(チ)& R=\omega L &(リ)& R=\frac {\omega L}{2} \\[ 5pt ]
&(ヌ)& \frac {\displaystyle \frac {3RE^{2}}{4}}{R^{2}+\left( \displaystyle \frac {\omega L}{2} \right) ^{2} } &(ル)& \frac {\displaystyle \frac {RE^{2}}{4}}{R^{2}+\left( 2\omega L \right) ^{2} } &(ヲ)& \frac {E}{\sqrt {3}} \\[ 5pt ]
&(ワ)& \mathrm {j}\omega L &(カ)& \frac {\sqrt {3}E}{2} &(ヨ)& \mathrm {j}\frac {\omega L}{2} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
1種の問5はほぼ三相交流回路から出題されます。
例年難易度差がとても大きく,令和2年度は比較的易しい問題であったと思います。
令和元年の問題や平成29年の問題等はかなり難易度が高い問題が出題されていますので,しっかりと対策をしていくようにしましょう。
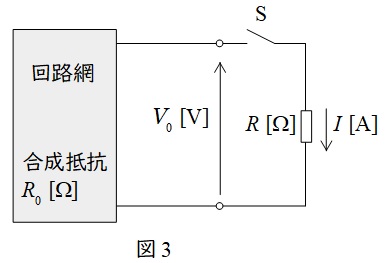
1.テブナンの定理
下図のような回路において,端子\( \ \mathrm {a-b} \ \)の開放電圧を\( \ V_{\mathrm {0}} \ \mathrm {[V]} \ \),端子\( \ \mathrm {a-b} \ \)から電源側をみた合成抵抗を\( \ R_{\mathrm {0}} \ \mathrm {[\Omega ]} \ \)とする(ただし,電圧源は短絡,電流源は開放する)と,図の抵抗\( \ R \ \mathrm {[\Omega ]} \ \)を流れる電流の大きさ\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I&=&\frac {V_{\mathrm {0}}}{R+R_{0}} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
※ テブナンの定理はコイルやコンデンサを含むインピーダンスでも同様に成立します。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ヨ
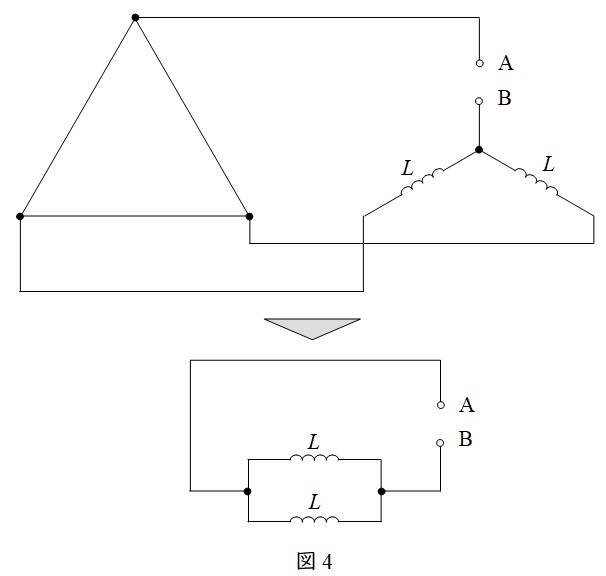
ワンポイント解説「1.テブナンの定理」の通り,図2のインピーダンス\( \ {\dot Z} \ \)は,端子\( \ \mathrm {A-B} \ \)から電源側を見た合成インピーダンスなので,図4の通りとなる。
したがって,合成インピーダンス\( \ {\dot Z} \ \)は,
\[
\begin{eqnarray}
\dot Z&=&\frac {\mathrm {j}\omega L\cdot \mathrm {j}\omega L}{\mathrm {j}\omega L+\mathrm {j}\omega L} \\[ 5pt ]
&=&\mathrm {j}\frac {\omega L}{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:カ
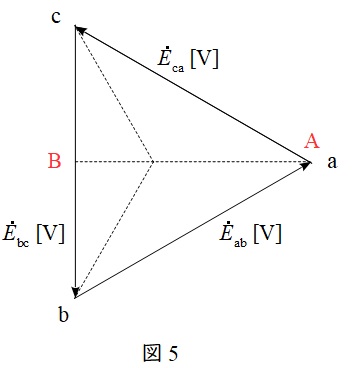
ワンポイント解説「1.テブナンの定理」の通り,図2の端子電圧\( \ \dot V \ \)の大きさ\( \ \left| \dot V \right| \ \)は,図1の端子\( \ \mathrm {A-B} \ \)の開放電圧となる。
端子\( \ \mathrm {A} \ \)の電位は\( \ \mathrm {a} \ \)の電位と等しく,端子\( \ \mathrm {B} \ \)の電位は端子\( \ \mathrm {b} \ \)と端子\( \ \mathrm {c} \ \)から共にインダクタ\( \ L \ \)を経由した中間電圧となる。したがって,端子\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)の電圧をベクトル図に示すと,図5のようになる。
図5より,三角形\( \ \mathrm {abc} \ \)が正三角形であることから,\( \ \mathrm {A-B} \ \)の開放電圧\( \ \left| \dot V \right| \ \)は,
\[
\begin{eqnarray}
\left| \dot V \right| &=&\frac {\sqrt {3}E}{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヘ
(1)及び(2)より,テブナンの定理を適用すると,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {R}}&=&\frac {\dot V}{R+\dot Z} \\[ 5pt ]
&=&\frac {\dot V}{\displaystyle R+\mathrm {j}\frac {\omega L}{2}} \\[ 5pt ]
\left| {\dot I}_{\mathrm {R}}\right| &=&\frac {\displaystyle \frac {\sqrt {3}E}{2}}{\displaystyle \sqrt {R^{2}+\left( \frac {\omega L}{2}\right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヌ
\( \ R \ \)で消費される有効電力\( \ P_{\mathrm {R}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {R}}&=&R\left| {\dot I}_{\mathrm {R}}\right| ^{2} \\[ 5pt ]
&=&R\left\{ \frac {\displaystyle \frac {\sqrt {3}E}{2}}{\displaystyle \sqrt {R^{2}+\left( \frac {\omega L}{2}\right) ^{2}}}\right\} ^{2} \\[ 5pt ]
&=&\frac {\displaystyle \frac {{3RE}^{2}}{4}}{R^{2}+\left( \displaystyle \frac {\omega L}{2} \right) ^{2} } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:リ
(4)より,
\[
\begin{eqnarray}
P_{\mathrm {R}}&=&\frac {\displaystyle \frac {{3E}^{2}}{4}}{R+\displaystyle \frac {\left( \displaystyle \frac {\omega L}{2} \right) ^{2}}{R} } \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ P_{\mathrm {R}} \ \)は最大となるためには,上式の分母\( \ A=R+\displaystyle \frac {\left( \displaystyle \frac {\omega L}{2} \right) ^{2}}{R} \ \)が最小となればよい。したがって,\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}R}=0 \ \)のとき,\( \ P_{\mathrm {R}} \ \)は最大となるので,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}R}=1-\displaystyle \frac {\left( \displaystyle \frac {\omega L}{2} \right) ^{2}}{R^{2}}&=&0 \\[ 5pt ]
\frac {\left( \displaystyle \frac {\omega L}{2} \right) ^{2}}{R^{2}}&=&1 \\[ 5pt ]
R^{2}&=&\left( \displaystyle \frac {\omega L}{2} \right) ^{2} \\[ 5pt ]
R&=& \frac {\omega L}{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん