【問題】
【難易度】★★★☆☆(普通)
次の文章は,演算増幅器を用いた回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。ただし,演算増幅器は理想的な特性であるとし,入力電圧の角周波数は\( \ \omega \ \)とする。
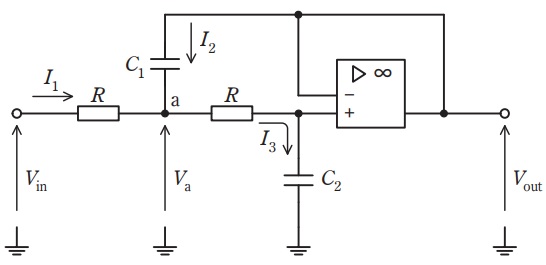
まず,図の回路の電圧増幅度\( \ \displaystyle \frac {V_{\mathrm {out}}}{V_{\mathrm {in}}} \ \)を求める。図中の\( \ I_{1} \ \),\( \ I_{2} \ \),\( \ I_{3} \ \)は入力電圧\( \ V_{\mathrm {in}} \ \),出力電圧\( \ V_{\mathrm {out}} \ \),節点\( \ \mathrm {a} \ \)の電位\( \ V_{\mathrm {a}} \ \)を用いてそれぞれ,
\[
\begin{eqnarray}
I_{1}&=&\frac {V_{\mathrm {in}}-V_{\mathrm {a}}}{R} &・・・・・・・・・・・・・・・・・・・・・・ ①& \\[ 5pt ]
I_{2}&=&\frac {V_{\mathrm {out}}-V_{\mathrm {a}}}{ \ \fbox { (1) } \ } &・・・・・・・・・・・・・・・・・・・・・・ ②& \\[ 5pt ]
I_{3}&=& \ \fbox { (2) } \ \times V_{\mathrm {out}} &・・・・・・・・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
と表せる。一方,\( \ I_{3} \ \)は\( \ V_{\mathrm {a}} \ \)を用いると,
\[
\begin{eqnarray}
I_{3}&=&\frac {V_{\mathrm {a}}}{\displaystyle R+\frac {1}{\mathrm {j}\omega C_{2}}} &・・・・・・・・・・・・・・・・・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
と表されるから,③式と④式より\( \ V_{\mathrm {a}} \ \)と\( \ V_{\mathrm {out}} \ \)の関係が得られる。この関係を用いると①式及び②式から\( \ V_{\mathrm {a}} \ \)が消去できる。\( \ I_{3}=I_{1}+I_{2} \ \)であることを考慮すると,①式,②式及び③式より回路の電圧増幅度\( \ \displaystyle \frac {V_{\mathrm {out}}}{V_{\mathrm {in}}} \ \)は,\( \ \mathrm {j}\omega \ \)を変数として,
\[
\begin{eqnarray}
\frac {V_{\mathrm {out}}}{V_{\mathrm {in}}}&=& \ \fbox { (3) } \ &・・・・・・・・・・・・・・・・・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
と書ける。
一般に,\( \ 2 \ \)次の低域通過フィルタの\( \ \displaystyle \frac {V_{\mathrm {out}}}{V_{\mathrm {in}}} \ \)は,回路のよさ\( \ Q \ \)と遮断角周波数\( \ \omega _{\mathrm {C}} \ \)を用いて,
\[
\begin{eqnarray}
\frac {V_{\mathrm {out}}}{V_{\mathrm {in}}}&=&\frac {{\omega _{\mathrm {C}}}^{2}}{\displaystyle \left( \mathrm {j}\omega \right) ^{2}+\frac {\omega _{\mathrm {C}}}{Q}\left( \mathrm {j}\omega \right) +{\omega _{\mathrm {C}}}^{2}} \ &・・・・・・・・・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
の形で表される。⑤式と⑥式の比較より,図の回路は,\( \ Q \ \)と遮断周波数\( \ f_{\mathrm {C}} \ \)がそれぞれ\( \ Q= \ \fbox { (4) } \ \)と\( \ \displaystyle f_{\mathrm {C}}=\frac {\omega _{\mathrm {C}}}{2\pi }=\frac {1}{2\pi R\sqrt {C_{1}C_{2}}} \ \)で表される\( \ 2 \ \)次の低域通過フィルタであることがわかる。
\( \ R=10 \ \mathrm {k\Omega } \ \)のとき,図の回路を\( \ \displaystyle Q=\frac {1}{\sqrt {2}} \ \),\( \ f_{\mathrm {C}}=1 \ \mathrm {kHz} \ \)の低域通過フィルタとするためには,\( \ C_{1} \ \)は\( \ \fbox { (5) } \ \mathrm {F} \ \)とすれば良い。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& \mathrm {j}\omega C_{1} &(ロ)& \frac {1}{\mathrm {j}\omega C_{1}} &(ハ)& R \\[ 5pt ]
&(ニ)& \frac {1}{R} &(ホ)& 11.2\times 10^{-9} &(ヘ)& \frac {1}{2}\sqrt {\frac {C_{2}}{C_{1}}} \\[ 5pt ]
&(ト)& \frac {1}{2}\sqrt {\frac {1}{C_{1}C_{2}}} &(チ)& \frac {1}{\mathrm {j}\omega C_{2}} &(リ)& 22.5\times 10^{-6} \\[ 5pt ]
&(ヌ)& 22.5\times 10^{-9} &(ル)& \frac {1}{2}\sqrt {\frac {C_{1}}{C_{2}}} &(ヲ)& \mathrm {j}\omega C_{2} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ワ)& \frac {1}{\displaystyle \left( \mathrm {j}\omega \right) ^{2}+\frac {2}{C_{1}R}\left( \mathrm {j}\omega \right) +\frac {1}{C_{1}C_{2}R^{2}}} \\[ 5pt ]
&(カ)& \frac {1}{\displaystyle C_{1}C_{2}R^{2}\left( \mathrm {j}\omega \right) ^{2}+2C_{1}R\left( \mathrm {j}\omega \right) +1} \\[ 5pt ]
&(ヨ)& \frac {1}{\displaystyle C_{1}C_{2}R^{2}\left( \mathrm {j}\omega \right) ^{2}+2C_{2}R\left( \mathrm {j}\omega \right) +1} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
演算増幅器を用いた回路の演算に関する問題です。
知識としては\( \ 3 \ \)種の頃から学習してきた内容のみですが,その場で考え高い計算力も必要とする問題となります。
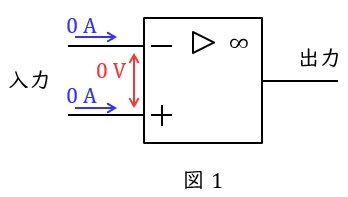
1.理想的な演算増幅器の特徴
1.電圧増幅率が無限大である。したがって,無限大でない有限数が出力される時,入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)(バーチャルショート)となる。
2.入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
3.出力インピーダンスがゼロである。
【解答】
(1)解答:ロ
問題図より,\( \ C_{1} \ \)に加わる電圧が\( \ V_{\mathrm {out}}-V_{\mathrm {a}} \ \)なので,
\[
\begin{eqnarray}
I_{2}&=&\frac {V_{\mathrm {out}}-V_{\mathrm {a}}}{\displaystyle \frac {1}{\mathrm {j}\omega C_{1}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ヲ
ワンポイント解説「1.理想的な演算増幅器の特徴」の通り,入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)なので,\( \ C_{2} \ \)に加わる電圧は\( \ V_{\mathrm {out}} \ \)となる。したがって,
\[
\begin{eqnarray}
I_{3}&=&\mathrm {j}\omega C_{2}V_{\mathrm {out}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヨ
(2)解答式及び④式より,
\[
\begin{eqnarray}
\mathrm {j}\omega C_{2}V_{\mathrm {out}}&=&\frac {V_{\mathrm {a}}}{\displaystyle R+\frac {1}{\mathrm {j}\omega C_{2}}} \\[ 5pt ]
V_{\mathrm {a}}&=&\mathrm {j}\omega C_{2}\left( R+\frac {1}{\mathrm {j}\omega C_{2}}\right) V_{\mathrm {out}} \\[ 5pt ]
&=&\left( 1+\mathrm {j}\omega C_{2}R\right) V_{\mathrm {out}} \\[ 5pt ]
\end{eqnarray}
\]
となり,これを①式及び②式((1)解答式)に代入すれば,
\[
\begin{eqnarray}
I_{1}&=&\frac {V_{\mathrm {in}}-\left( 1+\mathrm {j}\omega C_{2}R\right) V_{\mathrm {out}}}{R} &・・・・・・・・・・・・・ ①^{\prime }& \\[ 5pt ]
I_{2}&=&\frac {V_{\mathrm {out}}-\left( 1+\mathrm {j}\omega C_{2}R\right) V_{\mathrm {out}}}{\displaystyle \frac {1}{\mathrm {j}\omega C_{1}}} \\[ 5pt ]
&=&\mathrm {j}\omega C_{1}\times \left\{ V_{\mathrm {out}}-\left( 1+\mathrm {j}\omega C_{2}R\right) V_{\mathrm {out}}\right\} \\[ 5pt ]
&=&\mathrm {j}\omega C_{1}\times \left( -\mathrm {j}\omega C_{2}RV_{\mathrm {out}}\right) \\[ 5pt ]
&=&-\left( \mathrm {j}\omega \right) ^{2} C_{1}C_{2}RV_{\mathrm {out}} &・・・・・・・・・・・・・ ②^{\prime }& \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ I_{3}=I_{1}+I_{2} \ \)に上式と(2)解答式を代入すると,
\[
\begin{eqnarray}
\mathrm {j}\omega C_{2}V_{\mathrm {out}}&=&\frac {V_{\mathrm {in}}-\left( 1+\mathrm {j}\omega C_{2}R\right) V_{\mathrm {out}}}{R}-\left( \mathrm {j}\omega \right) ^{2} C_{1}C_{2}RV_{\mathrm {out}} \\[ 5pt ]
\left( \mathrm {j}\omega \right) ^{2} C_{1}C_{2}RV_{\mathrm {out}}+\mathrm {j}\omega C_{2}V_{\mathrm {out}}&=&\frac {V_{\mathrm {in}}-\left( 1+\mathrm {j}\omega C_{2}R\right) V_{\mathrm {out}}}{R} \\[ 5pt ]
\left( \mathrm {j}\omega \right) ^{2} C_{1}C_{2}R^{2}V_{\mathrm {out}}+\mathrm {j}\omega C_{2}RV_{\mathrm {out}}&=&V_{\mathrm {in}}-\left( 1+\mathrm {j}\omega C_{2}R\right) V_{\mathrm {out}} \\[ 5pt ]
\left( \mathrm {j}\omega \right) ^{2} C_{1}C_{2}R^{2}V_{\mathrm {out}}+2\left( \mathrm {j}\omega \right) C_{2}RV_{\mathrm {out}}+V_{\mathrm {out}}&=&V_{\mathrm {in}} \\[ 5pt ]
\left\{ \left( \mathrm {j}\omega \right) ^{2} C_{1}C_{2}R^{2}+2\left( \mathrm {j}\omega \right) C_{2}R+1\right\} V_{\mathrm {out}}&=&V_{\mathrm {in}} \\[ 5pt ]
\frac {V_{\mathrm {out}}}{V_{\mathrm {in}}}&=&\frac {1}{\left( \mathrm {j}\omega \right) ^{2} C_{1}C_{2}R^{2}+2\left( \mathrm {j}\omega \right) C_{2}R+1} \\[ 5pt ]
&=&\frac {1}{\displaystyle C_{1}C_{2}R^{2}\left( \mathrm {j}\omega \right) ^{2}+2C_{2}R\left( \mathrm {j}\omega \right) +1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
(3)解答式を⑥式の形に変形すると,
\[
\begin{eqnarray}
\frac {V_{\mathrm {out}}}{V_{\mathrm {in}}}&=&\frac {1}{\displaystyle C_{1}C_{2}R^{2}\left( \mathrm {j}\omega \right) ^{2}+2C_{2}R\left( \mathrm {j}\omega \right) +1} \\[ 5pt ]
&=&\frac {\displaystyle \frac {1}{C_{1}C_{2}R^{2}}}{\displaystyle \left( \mathrm {j}\omega \right) ^{2}+\frac {2}{C_{1}R}\left( \mathrm {j}\omega \right) +\frac {1}{C_{1}C_{2}R^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを⑥式と比較すれば,
\[
\begin{eqnarray}
\frac {2}{C_{1}R}&=&\frac {\omega _{\mathrm {C}}}{Q} &・・・・・・・・・・・・・・・・・・・・・・・・ ⑦& \\[ 5pt ]
\frac {1}{C_{1}C_{2}R^{2}}&=&{\omega _{\mathrm {C}}}^{2} &・・・・・・・・・・・・・・・・・・・・・・・・ ⑧& \\[ 5pt ]
\end{eqnarray}
\]
となるので,⑧式より,
\[
\begin{eqnarray}
\omega _{\mathrm {C}}&=&\frac {1}{R\sqrt {C_{1}C_{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるから,これを⑦式に代入すれば,
\[
\begin{eqnarray}
\frac {2}{C_{1}R}&=&\frac {\displaystyle \frac {1}{R\sqrt {C_{1}C_{2}}}}{Q} \\[ 5pt ]
Q&=&\frac {1}{R\sqrt {C_{1}C_{2}}}\times \frac {C_{1}R}{2} \\[ 5pt ]
&=&\frac {1}{2}\sqrt {\frac {C_{1}}{C_{2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヌ
⑦式に\( \ R=10 \ \mathrm {[k\Omega ]} \ \),\( \ \displaystyle Q=\frac {1}{\sqrt {2}} \ \),\( \ f_{\mathrm {C}}=1 \ \mathrm {[kHz]} \ \)を代入すると,
\[
\begin{eqnarray}
\frac {2}{C_{1}R}&=&\frac {2\pi f_{\mathrm {C}}}{Q} \\[ 5pt ]
\frac {2}{C_{1}\times 10\times 10^{3}}&=&\frac {2\pi \times 1\times 10^{3}}{\displaystyle \frac {1}{\sqrt {2}}} \\[ 5pt ]
C_{1}&=&\frac {2}{10\times 10^{3}}\times \frac {\displaystyle \frac {1}{\sqrt {2}}}{2\pi \times 1\times 10^{3}} \\[ 5pt ]
&≒&22.5\times 10^{-9} \ \mathrm {[F]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん