【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,三相交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な数値を解答群の中から選び,その記号をマークシートに記入しなさい。
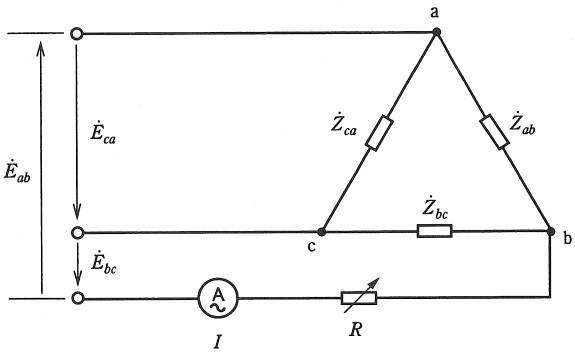
図のように,実効値が\( \ 220 \ \mathrm {[V]} \ \)である対称三相電源\( \ {\dot E}_{ab} = 220∠0° \ \mathrm {[V]} \ \),\( \ {\dot E}_{bc} = 220∠-120° \ \mathrm {[V]} \ \),\( \ {\dot E}_{ca} = 220∠-240° \ \mathrm {[V]} \ \)が,\( \ \Delta \ \)形三相負荷と一つの可変抵抗からなる回路に接続されている。この\( \ \Delta \ \)形三相負荷の各相のインピーダンスは\( \ {\dot Z}_{ab} ={\dot Z}_{bc} = 66+\mathrm {j}54 \ \mathrm {[\Omega ]} \ \),\( \ {\dot Z}_{ca} = 106+\mathrm {j}50 \ \mathrm {[\Omega ]} \ \)である。この回路には,実効値を指示する\( \ 1 \ \)個の理想的な交流電流計が図のように接続されており,その指示値を\( \ I \ \)とする。
いま,可変抵抗値を\( \ R=0 \ \mathrm {[\Omega ]} \ \)とした場合,電流計の指示値は,\( \ I= \ \fbox { (1) } \ \mathrm {[A]} \ \)となり,負荷の三相電力は\( \ \fbox { (2) } \ \mathrm {[kW]} \ \)となる。
次に,可変抵抗を調整したところ,各線電流の大きさは同じ値となり,回路は全体で平衡状態となった。この場合,可変抵抗の調整値は,\( \ R= \ \fbox { (3) } \ \mathrm {[\Omega ]} \ \)であり,電流計の指示値は,\( \ I= \ \fbox { (4) } \ \mathrm {[A]} \ \)である。また,可変抵抗と\( \ \Delta \ \)形三相負荷からなる回路の総電力は,\( \ \fbox { (5) } \ \mathrm {[kW]} \ \)である。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& 6.29 &(ロ)& 0.396 &(ハ)& 3.63 \\[ 5pt ]
&(ニ)& 15 &(ホ)& 4.47 &(ヘ)& 7.5 \\[ 5pt ]
&(ト)& 0.461 &(チ)& 12 &(リ)& 1.25 \\[ 5pt ]
&(ヌ)& 0.521 &(ル)& 1.19 &(ヲ)& 30 \\[ 5pt ]
&(ワ)& 0.185 &(カ)& 8.36 &(ヨ)& 2.08 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
不平衡負荷を接続した三相交流回路に関する問題です。
回路の考え方はそれほど難解ではありませんが,(3)以降の計算量が多く,選択肢も絞れないため問2の配点から考えるとかなり厳しい問題です。
本番で直面した場合には,一旦飛ばして後から戻る形が良いかと思います。
1.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータ\( \ a \ \)は,\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ]
&=& 1 \\[ 5pt ]
\end{eqnarray}
\]
となります。上記より,
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ]
1+a+a^{2}&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかります。
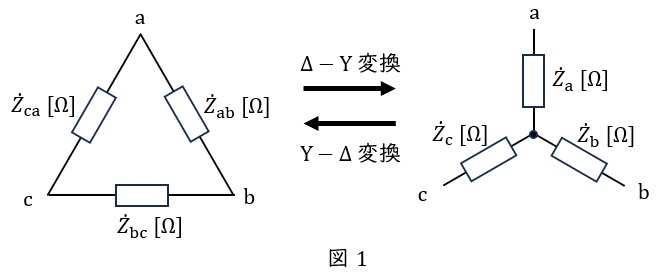
2.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
図1において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \mathrm {Y}-\Delta \ \)変換
図1において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}&=&{\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ホ
ワンポイント解説「1.ベクトルオペレータ\( \ a \ \)」の通り,\( \ {\dot E}_{ab} = 220 \ \mathrm {[V]} \ \),\( \ {\dot E}_{bc} = 220a^{2} \ \mathrm {[V]} \ \),\( \ {\dot E}_{ca} = 220a \ \mathrm {[V]} \ \)とおく。\( \ R=0 \ \mathrm {[\Omega ]} \ \)のとき,各インピーダンスを流れる電流\( \ {\dot I}_{ab} \ \mathrm {[A]} \ \),\( \ {\dot I}_{bc} \ \mathrm {[A]} \ \),\( \ {\dot I}_{ca} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{ab} &=& \frac {{\dot E}_{ab}}{{\dot Z}_{ab}} \\[ 5pt ]
&=& \frac {220}{66+\mathrm {j}54} \ \mathrm {[A]} \\[ 5pt ]
{\dot I}_{bc} &=& \frac {{\dot E}_{bc}}{{\dot Z}_{bc}} \\[ 5pt ]
&=& \frac {220a^{2}}{66+\mathrm {j}54} \ \mathrm {[A]} \\[ 5pt ]
{\dot I}_{ca} &=& \frac {{\dot E}_{ca}}{{\dot Z}_{ca}} \\[ 5pt ]
&=& \frac {220a}{106+\mathrm {j}50} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,電流計を流れる電流\( \ \dot I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
\dot I &=& {\dot I}_{bc}-{\dot I}_{ab} \\[ 5pt ]
&=& \frac {220a^{2}}{66+\mathrm {j}54}-\frac {220}{66+\mathrm {j}54} \\[ 5pt ]
&=& \frac {220}{66+\mathrm {j}54}\left( a^{2}-1 \right) \\[ 5pt ]
&=& \frac {220}{66+\mathrm {j}54}\left( -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2}-1 \right) \\[ 5pt ]
&=& \frac {220}{66+\mathrm {j}54}\left( -\frac {3+\mathrm {j}\sqrt {3}}{2} \right) \\[ 5pt ]
&=& -\frac {110\left( 3+\mathrm {j}\sqrt {3}\right) }{66+\mathrm {j}54} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その大きさ\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I &=& \left| -\frac {110\left( 3+\mathrm {j}\sqrt {3}\right) }{66+\mathrm {j}54} \right| \\[ 5pt ]
&=& \frac {110\sqrt {3^{2}+\left( \sqrt {3}\right) ^{2}}}{\sqrt {66^{2}+54^{2}}} \\[ 5pt ]
&=& \frac {110\sqrt {12}}{\sqrt {7 \ 272}} \\[ 5pt ]
&=& \frac {110}{\sqrt {606}} \\[ 5pt ]
&≒&4.4684 → 4.47 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:リ
各インピーダンスを流れる電流の大きさ\( \ I_{ab} \ \mathrm {[A]} \ \),\( \ I_{bc} \ \mathrm {[A]} \ \),\( \ I_{ca} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{ab} &=& \left| \frac {220}{66+\mathrm {j}54}\right| \\[ 5pt ]
&=& \frac {220}{\sqrt {66^{2}+54^{2}}} \ \mathrm {[A]} \\[ 5pt ]
&≒& 2.579 \ 9 \ \mathrm {[A]} \\[ 5pt ]
I_{bc} &=& \left| \frac {220a^{2}}{66+\mathrm {j}54}\right| \\[ 5pt ]
&=& \frac {220}{\sqrt {66^{2}+54^{2}}} \ \mathrm {[A]} \\[ 5pt ]
&≒& 2.579 \ 9 \ \mathrm {[A]} \\[ 5pt ]
I_{ca} &=& \left| \frac {220a}{106+\mathrm {j}50}\right| \\[ 5pt ]
&=& \frac {220}{\sqrt {106^{2}+50^{2}}} \ \mathrm {[A]} \\[ 5pt ]
&≒& 1.877 \ 1 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,負荷の三相電力\( \ P \ \mathrm {[kW]} \ \)は,それぞれの負荷の抵抗分が\( \ R_{ab} =R_{bc} = 66 \ \mathrm {[\Omega ]} \ \),\( \ R_{ca} = 106 \ \mathrm {[\Omega ]} \ \)なので,
\[
\begin{eqnarray}
P &=& R_{ab}{I_{ab}}^{2}+R_{bc}{I_{bc}}^{2}+R_{ca}{I_{ca}}^{2} \\[ 5pt ]
&=& 66\times 2.579 \ 9^{2}+66\times 2.579 \ 9^{2}+106\times 1.877 \ 1^{2} \\[ 5pt ]
&≒& 1 \ 252.1 \ \mathrm {[W]} → 1.25 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:チ
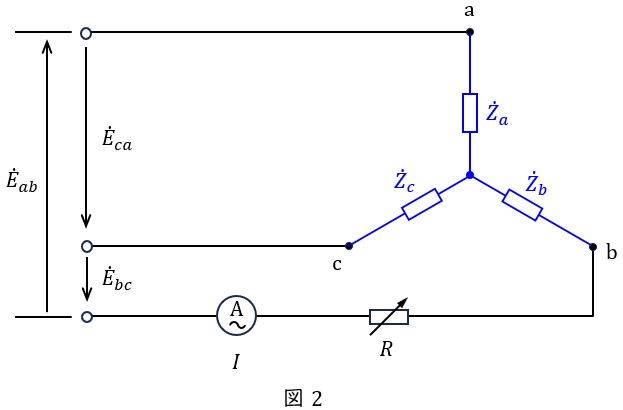
図2のように,三相不平衡負荷を\( \ \Delta -\mathrm {Y} \ \)変換したときの各インピーダンス\( \ {\dot Z}_{a} \ \mathrm {[\Omega ]} \ \),\( \ {\dot Z}_{b} \ \mathrm {[\Omega ]} \ \),\( \ {\dot Z}_{c} \ \mathrm {[\Omega ]} \ \)は,ワンポイント解説「2.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り,
\[
\begin{eqnarray}
{\dot Z}_{a}&=&\frac {{\dot Z}_{ab}{\dot Z}_{ca}}{{\dot Z}_{ab}+{\dot Z}_{bc}+{\dot Z}_{ca}} \\[ 5pt ]
&=&\frac {\left( 66+\mathrm {j}54\right) \left( 106+\mathrm {j}50\right) }{\left( 66+\mathrm {j}54\right) +\left( 66+\mathrm {j}54\right) +\left( 106+\mathrm {j}50\right) } \\[ 5pt ]
&=&\frac {6 \ 996-2 \ 700+\mathrm {j}\left( 5 \ 724+3 \ 300\right) }{238+\mathrm {j}158} \\[ 5pt ]
&=&\frac {4 \ 296+\mathrm {j}9 \ 024}{238+\mathrm {j}158} \\[ 5pt ]
&=&\frac {4 \ 296+\mathrm {j}9 \ 024}{238+\mathrm {j}158}\times \frac {238-\mathrm {j}158}{238-\mathrm {j}158} \\[ 5pt ]
&≒&\frac {1 \ 022 \ 400+1 \ 425 \ 800+\mathrm {j}\left( -678 \ 770+2 \ 147 \ 700\right) }{56 \ 644+24 \ 964} \\[ 5pt ]
&≒&\frac {2 \ 448 \ 200+\mathrm {j}1 \ 468 \ 900 }{81 \ 608} \\[ 5pt ]
&≒&30.000+\mathrm {j}17.999 \ \mathrm {[\Omega ]} \\[ 5pt ]
{\dot Z}_{b}&=&\frac {{\dot Z}_{bc}{\dot Z}_{ab}}{{\dot Z}_{ab}+{\dot Z}_{bc}+{\dot Z}_{ca}} \\[ 5pt ]
&=&\frac {\left( 66+\mathrm {j}54\right) \left( 66+\mathrm {j}54\right) }{\left( 66+\mathrm {j}54\right) +\left( 66+\mathrm {j}54\right) +\left( 106+\mathrm {j}50\right) } \\[ 5pt ]
&=&\frac {4 \ 356-2 \ 916+\mathrm {j}\left( 3 \ 564+3 \ 564\right) }{238+\mathrm {j}158} \\[ 5pt ]
&=&\frac {1 \ 440+\mathrm {j}7 \ 128 }{238+\mathrm {j}158} \\[ 5pt ]
&=&\frac {1 \ 440+\mathrm {j}7 \ 128 }{238+\mathrm {j}158}\times \frac {238-\mathrm {j}158}{238-\mathrm {j}158} \\[ 5pt ]
&≒&\frac {342 \ 720+1 \ 126 \ 200+\mathrm {j}\left( -227 \ 520+1 \ 696 \ 500\right) }{56 \ 644+24 \ 964} \\[ 5pt ]
&≒&\frac {1 \ 468 \ 900+\mathrm {j}1 \ 469 \ 000 }{81 \ 608} \\[ 5pt ]
&≒&17.999+\mathrm {j}18.001 \ \mathrm {[\Omega ]} \\[ 5pt ]
{\dot Z}_{c}&=&\frac {{\dot Z}_{ca}{\dot Z}_{bc}}{{\dot Z}_{ab}+{\dot Z}_{bc}+{\dot Z}_{ca}} \\[ 5pt ]
&=&\frac {\left( 106+\mathrm {j}50\right) \left( 66+\mathrm {j}54\right) }{\left( 66+\mathrm {j}54\right) +\left( 66+\mathrm {j}54\right) +\left( 106+\mathrm {j}50\right) } \\[ 5pt ]
&≒&30.000+\mathrm {j}17.999 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,三相平衡となったときの可変抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の大きさは,\( \ {\dot Z}_{a} \ \mathrm {[\Omega ]} \ \)及び\( \ {\dot Z}_{c} \ \mathrm {[\Omega ]} \ \)の抵抗分\( \ R_{a}=R_{c}=30.000 \ \mathrm {[\Omega ]} \ \),\( \ {\dot Z}_{b} \ \mathrm {[\Omega ]} \ \)の抵抗分\( \ R_{b}=17.999 \ \mathrm {[\Omega ]} \ \)より,
\[
\begin{eqnarray}
R &=&R_{a}-R_{b} \\[ 5pt ]
&=&30.000-17.999 \\[ 5pt ]
&≒& 12.001 → 12.0 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ハ
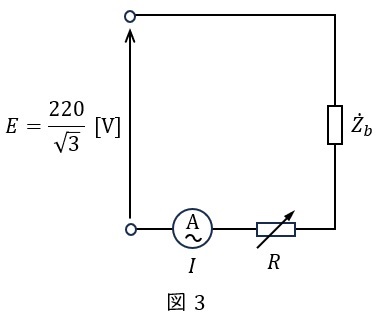
三相平衡となったので,一相分等価回路は図3のようになる。
図3より電流計の指示値\( \ I \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I &=&\frac {E}{\left| {\dot Z}_{\mathrm {b}}+R\right|} \\[ 5pt ]
&=&\frac {\displaystyle \frac {220}{\sqrt {3}}}{\left| 17.999+\mathrm {j}18.001+12.001\right|} \\[ 5pt ]
&=&\frac {220}{\sqrt {3}\left| 30.000+\mathrm {j}18.001 \right|} \\[ 5pt ]
&=&\frac {220}{\sqrt {3}\sqrt {30.000^{2}+18.001^{2}}} \\[ 5pt ]
&≒& 3.630 \ 4 → 3.63 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ル
(3)及び(4)より,全体の総電力\( \ P^{\prime } \ \mathrm {[kW]} \ \)は,
\[
\begin{eqnarray}
P^{\prime } &=& 3\left( R_{b}+R\right) I^{2} \\[ 5pt ]
&=& 3\times \left( 17.999+12.001\right) \times 3.630 \ 4^{2} \\[ 5pt ]
&≒& 1 \ 186.2 \ \mathrm {[W]} → 1.19 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん