【問題】
【難易度】★★★☆☆(普通)
次の文章は,円形コイルの作る磁界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
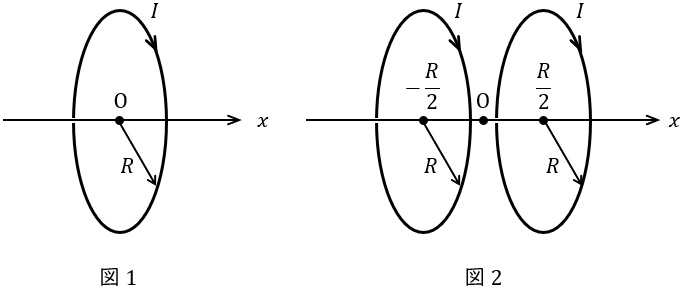
真空中において半径\( \ R \ \)で一巻きの円形コイルに電流\( \ I \ \)が流れている。図1のように\( \ x \ \)軸の原点\( \ \mathrm {O} \ \)に円形コイルの中心があり,\( \ x \ \)軸上に正の向きの磁束を生じるように置かれているときの\( \ x \ \)軸上の磁束密度の大きさ\( \ B\left( x\right) \ \)は,ビオ・サバールの法則により次のように求められる。ただし,\( \ \mu _{0} \ \)は真空中の透磁率である。
\[
\begin{eqnarray}
B\left( x\right) &=& \frac {\mu _{0}IR^{2}}{2\left( x^{2}+R^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ]
\end{eqnarray}
\]
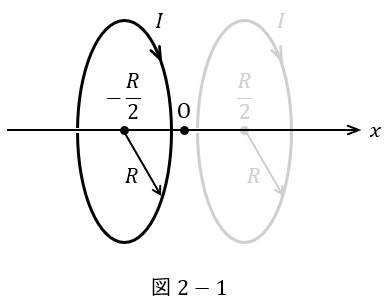
次に,この円形コイル二つを図2のように原点\( \ \mathrm {O} \ \)に対称に距離\( \ R \ \)だけ離して置く。このコイルをヘルムホルツコイル\( \ \left( \mathrm {Helmholtz \ coil}\right) \ \)という。ここで,ヘルムホルツコイルの\( \ x \ \)軸上の磁束密度の大きさ\( \ B_{\mathrm {H}}\left( x\right) \ \)について考察する。
\( \ B_{\mathrm {H}}\left( x\right) \ \)を\( \ B\left( x\right) \ \)で表すと,\( \ \fbox { (1) } \ \)である。
ここで,\( \ B_{\mathrm {H}}\left( x\right) \ \)を次のようにマクローリン展開することを考える。ただし,\( \ {B_{\mathrm {H}}}^{\left( n\right) }\left( x\right) \ \)は\( \ B_{\mathrm {H}}\left( x\right) \ \)の\( \ n \ \)階微分を表す。
\[
\begin{eqnarray}
B_{\mathrm {H}}\left( x\right) &=& B_{\mathrm {H}}\left( 0\right) +{B_{\mathrm {H}}}^{\prime }\left( 0\right) x+\frac {{B_{\mathrm {H}}}^{\prime \prime }\left( 0\right) }{2!}x^{2}+\cdots +\frac {{B_{\mathrm {H}}}^{\left( n\right) }\left( 0\right) }{n!}x^{n}+\cdots \\[ 5pt ]
\end{eqnarray}
\]
まず,\( \ x \ \)の\( \ 2 \ \)乗の項を取り出して考えると,\( \ {B_{\mathrm {H}}}^{\prime \prime }\left( 0\right) = \ \fbox { (2) } \ \)である。
\( \ \displaystyle \left( 関数 \ f(x) =\frac {1}{\left( x^{2}+a^{2}\right) ^{\frac {3}{2}}} \ について, \ f^{\prime \prime }(x) =\frac {12x^{2}-3a^{2}}{\left( x^{2}+a^{2}\right) ^{\frac {7}{2}}} \ である。 \ \right) \ \)
一方,\( \ B\left( x\right) \ \)は\( \ B\left( -x\right) =B\left( x\right) \ \)が成り立つため,偶関数である。したがって,\( \ B_{\mathrm {H}}\left( x\right) \ \)は\( \ \fbox { (3) } \ \)である。このため,\( \ x \ \)の奇数乗の項は全てゼロとなる。
これまでの考察で,マクローリン展開した項のうち,定数項を除き,\( \ x \ \)の\( \ \fbox { (4) } \ \)の項までがゼロになることが分かった。このことから,ヘルムホルツコイルを用いると原点近傍で\( \ \fbox { (5) } \ \)磁界が得られることが分かる。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& x \ に比例する &(ロ)& 急峻に変化する &(ハ)& ほぼ一定の \\[ 5pt ]
&(ニ)& 1 \ 乗 &(ホ)& 2 \ 乗 &(ヘ)& 3 \ 乗 \\[ 5pt ]
&(ト)& 奇関数 &(チ)& 偶関数 &(リ)& 0 \\[ 5pt ]
&(ヌ)& \frac {144\sqrt {2}}{R^{3}}\mu _{0}I &(ル)& \frac {216}{R^{3}}\mu _{0}I &(ヲ)& B\left( x+R\right) +B\left( x-R\right) \\[ 5pt ]
&(ワ)& \sqrt {2}B\left( x\right) &(カ)& 2B\left( x \right) &(ヨ)& B\left( x+\frac {R}{2}\right) +B\left( x-\frac {R}{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
二つの円形コイルが作る磁界の大きさを考える問題です。
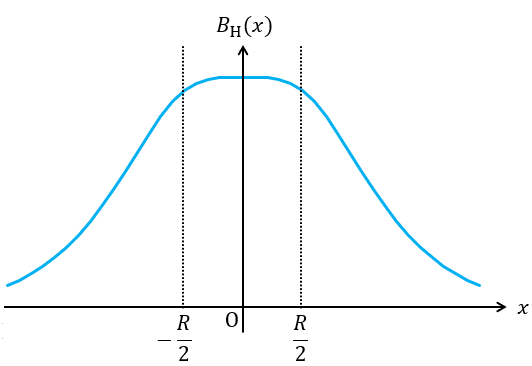
(1)で導出できる式のグラフを実際に描くと下図のようになりますが,問題を見ながら右ねじの法則等で磁束密度(磁界の大きさ)の概要をイメージできると特に計算をしなくても(2)以降の解答が類推できるかと思います。
1.偶関数と奇関数
①偶関数
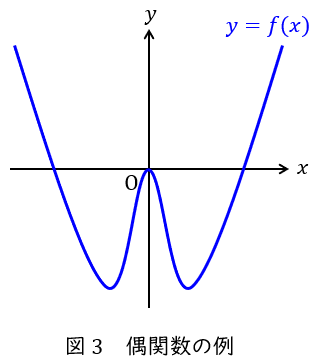
偶関数は図3のように,\( \ y \ \)軸を軸として左右対称となる関数のことをいい,\( \ f\left( -x \right) =f\left( x \right) \ \)の関係があります。
一般に\( \ y=f\left( x \right) \ \)が偶数乗の項のみで構成されるもの(例:\( \ y=x^{4}-2x^{2}+3 \ \))が偶関数となります。三角関数の\( \ \displaystyle y=\cos x=1-\frac {x^{2}}{2!}+\frac {x^{4}}{4!}-\cdots \ \)等も偶関数の一つです。
②奇関数
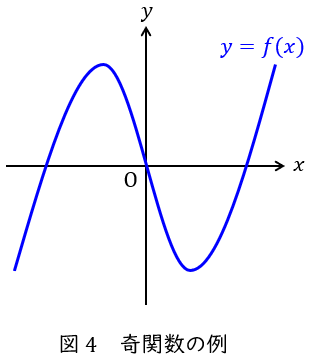
奇関数は図4のように,原点\( \ \mathrm {O} \ \)を中心とした点対称となる関数のことをいい,\( \ f\left( -x \right) =-f\left( x \right) \ \)の関係があります。
一般に\( \ y=f\left( x \right) \ \)が奇数乗の項のみで構成されるもの(例:\( \ y=x^{5}-2x^{3}-3x \ \))が奇関数となります。三角関数の\( \ \displaystyle y=\sin x=x-\frac {x^{3}}{3!}+\frac {x^{5}}{5!}-\cdots \ \)等も奇関数の一つです。
【解答】
(1)解答:ヨ
図2-1に示すように,まず\( \ \displaystyle x=-\frac {R}{2} \ \)に中心がある円形コイルについて考えると,\( \ x \ \)軸上の磁束密度の大きさは,
\[
\begin{eqnarray}
B\left( x+\frac {R}{2}\right) &=& \frac {\mu _{0}IR^{2}}{2\left\{ \left( x+\displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {3}{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。同様に,\( \ \displaystyle x=\frac {R}{2} \ \)に中心がある円形コイルの\( \ x \ \)軸上の磁束密度の大きさは,
\[
\begin{eqnarray}
B\left( x-\frac {R}{2}\right) &=& \frac {\mu _{0}IR^{2}}{2\left\{ \left( x-\displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {3}{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ヘルムホルツコイルの\( \ x \ \)軸上の磁束密度の大きさ\( \ B_{\mathrm {H}}\left( x\right) \ \)は,
\[
\begin{eqnarray}
B_{\mathrm {H}}\left( x\right) &=&B\left( x+\frac {R}{2}\right) +B\left( x-\frac {R}{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:リ
与えられている\( \ 2 \ \)階微分の公式より,
\[
\begin{eqnarray}
{B_{\mathrm {H}}}^{\prime \prime}\left( x\right) &=&\left[ \frac {\mu _{0}IR^{2}}{2\left\{ \left( x+\displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {3}{2}}}+\frac {\mu _{0}IR^{2}}{2\left\{ \left( x-\displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {3}{2}}}\right] ^{\prime \prime } \\[ 5pt ]
&=&\frac {\mu _{0}IR^{2}}{2}\left[ \frac {1}{\left\{ \left( x+\displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {3}{2}}}+\frac {1}{\left\{ \left( x-\displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {3}{2}}}\right] ^{\prime \prime } \\[ 5pt ]
&=&\frac {\mu _{0}IR^{2}}{2}\left[ \frac {12\left( x+\displaystyle \frac {R}{2}\right) ^{2}-3R^{2}}{\left\{ \left( x+\displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {7}{2}}} +\frac {12\left( x-\displaystyle \frac {R}{2}\right) ^{2}-3R^{2}}{\left\{ \left( x-\displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {7}{2}}}\right] \\[ 5pt ]
\end{eqnarray}
\]
となるから,\( \ {B_{\mathrm {H}}}^{\prime \prime }\left( 0\right) \ \)は,
\[
\begin{eqnarray}
{B_{\mathrm {H}}}^{\prime \prime}\left( 0\right) &=&\frac {\mu _{0}IR^{2}}{2}\left[ \frac {12\left( \displaystyle \frac {R}{2}\right) ^{2}-3R^{2}}{\left\{ \left( \displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {7}{2}}} +\frac {12\left( -\displaystyle \frac {R}{2}\right) ^{2}-3R^{2}}{\left\{ \left( -\displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {7}{2}}}\right] \\[ 5pt ]
&=&\frac {\mu _{0}IR^{2}}{2}\left[ \frac {3R^{2}-3R^{2}}{\left\{ \left( \displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {7}{2}}} +\frac {3R^{2}-3R^{2}}{\left\{ \left( -\displaystyle \frac {R}{2}\right) ^{2}+R^{2}\right\} ^{\frac {7}{2}}}\right] \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:チ
\( \ B_{\mathrm {H}}\left( x\right) \ \)においても,原点\( \ \mathrm {O} \ \)を基準に左右対称とした関数となるので偶関数となり,\( \ x \ \)の奇数乗の項は全てゼロとなる。
(4)解答:ヘ
(2)及び(3)より,\( \ x \ \)の\( \ 3 \ \)乗の項までがゼロとなることがわかる。
(5)解答:ハ
原点付近で微分した値が零であることから,磁界は原点付近でほぼ一定の磁界となることがわかる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん