《理論》〈電気回路〉[H23:問3]三相回路における各電流及び電力の導出に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，三相回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。

図に示すように，抵抗$ \ R \ $，容量性リアクタンス$ \ X \ $，誘導性リアクタンス$ \ X \ $からなる不平衡三相負荷と二つの単相電力計$ \ 1 \ $と$ \ 2 \ $を接続した回路がある。ただし，単相電力計は理想的とする。

端子$ \ \mathrm {a} \ $，$ \ \mathrm {b} \ $，$ \ \mathrm {c} \ $に相回転が$ \ \mathrm {abc} \ $の順で線間電圧$ \ V \ $の対称三相電圧を印加した。このとき，$ \ \dot V_{\mathrm {ab}} \ $を基準（$ \ \dot V_{\mathrm {ab}}=V ∠0^{\circ } \ $）とすると線電流$ \ \dot I_{\mathrm {a}} \ $，$ \ \dot I_{\mathrm {b}} \ $，$ \ \dot I_{\mathrm {c}} \ $はそれぞれ
\[
\begin{eqnarray}
\dot I_{\mathrm {a}}= \ \fbox {　（１）　} \\[ 5pt ] \dot I_{\mathrm {b}}= \ \fbox {　（２）　} \\[ 5pt ] \dot I_{\mathrm {c}}= \ \fbox {　（３）　} \\[ 5pt ] \end{eqnarray}
\] となる。
次に，抵抗$ \ R \ $を変化させ，$ \ R \ $を$ \ \fbox {　（４）　} \ $にしたところ，対称三相の線電流$ \ \dot I_{\mathrm {a}} \ $，$ \ \dot I_{\mathrm {b}} \ $，$ \ \dot I_{\mathrm {c}} \ $が流れた。このとき，電力計$ \ 1 \ $，$ \ 2 \ $の指示$ \ W_{1} \ $，$ \ W_{2} \ $は$ \ \fbox {　（５）　} \ $となる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\sqrt {3}X　　　&（ロ）&　\left[ \left( \frac {1}{R}-\frac {\sqrt {3}}{2X}\right) -\mathrm {j}\frac {1}{X}\right] V \\[ 5pt ] &（ハ）&　\left[ -\left( \frac {1}{R}-\frac {\sqrt {3}}{2X}\right) -\mathrm {j}\frac {1}{2X}\right] V　　　&（ニ）&　\frac {1}{\sqrt {3}}X \\[ 5pt ] &（ホ）&　\left[ \left( \frac {1}{R}-\frac {\sqrt {3}}{2X}\right) +\mathrm {j}\frac {1}{2X}\right] V　　　&（ヘ）&　\frac {2}{\sqrt {3}}X \\[ 5pt ] &（ト）&　\left[ -\left( \frac {1}{R}-\frac {\sqrt {3}}{2X}\right) +\mathrm {j}\frac {1}{2X}\right] V　　　&（チ）&　-\mathrm {j}\frac {1}{X}V \\[ 5pt ] &（リ）&　W_{1}=\frac {\sqrt {3}}{2X}V^{2},W_{2}=\frac {\sqrt {3}}{2X}V^{2}　　　&（ヌ）&　\left[ -\left( \frac {1}{R}-\frac {\sqrt {3}}{2X}\right) -\mathrm {j}\frac {1}{X}\right] V \\[ 5pt ] &（ル）&　W_{1}=\frac {2\sqrt {3}}{X}V^{2},W_{2}=-\frac {\sqrt {3}}{X}V^{2}　　　&（ヲ）&　\left[ \left( \frac {1}{R}-\frac {\sqrt {3}}{2X}\right) -\mathrm {j}\frac {1}{2X}\right] V \\[ 5pt ] &（ワ）&　\mathrm {j}\frac {1}{X}V　　　&（カ）&　W_{1}=\frac {\sqrt {3}}{X}V^{2},W_{2}=0 \\[ 5pt ] &（ヨ）&　\mathrm {j}\frac {1}{2X}V
\end{eqnarray}
\]

【ワンポイント解説】

三相回路の電流と電力を求める問題です。
一見難しそうに見えますが，$ \ 1 \ $種の三相交流の問題としてはかなり易しい問題です。しっかりと解法をマスターして確実に得点できるようにしましょう。

【解答】

(1)解答：ヲ
(2)解答：ハ
(3)解答：ワ
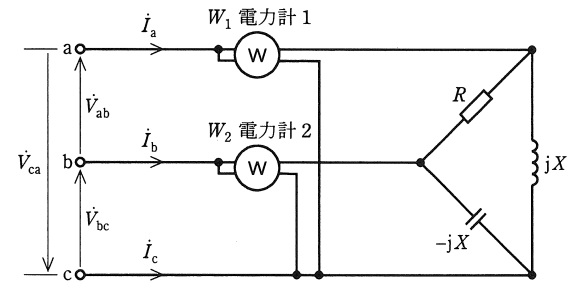
$ \ {\dot V}_{\mathrm {ab}}=V ∠0^{\circ } \ $とすると，$ \ {\dot V}_{\mathrm {bc}} \ $，$ \ {\dot V}_{\mathrm {ca}} \ $は図1に示す通り，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {bc}}&=&V ∠240^{\circ}&=&\frac {-1-\mathrm {j}\sqrt {3}}{2}V \\[ 5pt ] {\dot V}_{\mathrm {ca}}&=&V ∠120^{\circ}&=&\frac {-1+\mathrm {j}\sqrt {3}}{2}V \\[ 5pt ] \end{eqnarray}
\] と表される。

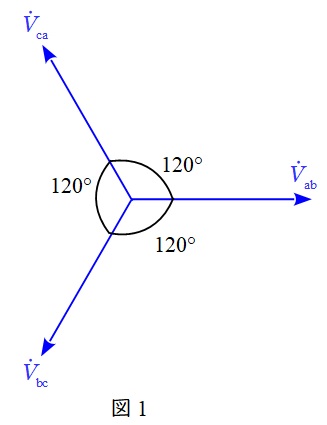
また，図2の通り$ \ {\dot I}_{\mathrm {ab}} \ $，$ \ {\dot I}_{\mathrm {bc}} \ $，$ \ {\dot I}_{\mathrm {ca}} \ $を定めると，オームの法則より各電流は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {ab}}&=&\frac{\dot V_{\mathrm {ab}}}{R} \\[ 5pt ] &=&\frac{V}{R} \\[ 5pt ] {\dot I}_{\mathrm {bc}}&=&\frac{\dot V_{\mathrm {bc}}}{-\mathrm {j}X} \\[ 5pt ] &=&\frac{\displaystyle \frac {-1-\mathrm {j}\sqrt {3}}{2}V}{-\mathrm {j}X} \\[ 5pt ] &=&\left( \frac {\sqrt {3}}{2X}-\mathrm {j}\frac {1}{2X}\right)V \\[ 5pt ] {\dot I}_{\mathrm {ca}}&=&\frac{\dot V_{\mathrm {ca}}}{\mathrm {j}X} \\[ 5pt ] &=&\frac{\displaystyle \frac {-1+\mathrm {j}\sqrt {3}}{2}V}{\mathrm {j}X} \\[ 5pt ] &=&\left( \frac {\sqrt {3}}{2X}+\mathrm {j}\frac {1}{2X}\right)V \\[ 5pt ] \end{eqnarray}
\] となる。これより，各相の電流$ \ {\dot I}_{\mathrm {a}} \ $，$ \ {\dot I}_{\mathrm {b}} \ $，$ \ {\dot I}_{\mathrm {c}} \ $は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}}&=&\dot I_{\mathrm {ab}}-\dot I_{\mathrm {ca}} \\[ 5pt ] &=&\frac{V}{R}-\left( \frac {\sqrt {3}}{2X}+\mathrm {j}\frac {1}{2X}\right)V \\[ 5pt ] &=&\left[ \left( \frac {1}{R}-\frac {\sqrt {3}}{2X}\right) -\mathrm {j}\frac {1}{2X}\right] V \\[ 5pt ] {\dot I}_{\mathrm {b}}&=&\dot I_{\mathrm {bc}}-\dot I_{\mathrm {ab}} \\[ 5pt ] &=&\left( \frac {\sqrt {3}}{2X}-\mathrm {j}\frac {1}{2X}\right)V-\frac{V}{R} \\[ 5pt ] &=&\left[ -\left( \frac {1}{R}-\frac {\sqrt {3}}{2X}\right) -\mathrm {j}\frac {1}{2X}\right] V \\[ 5pt ] {\dot I}_{\mathrm {c}}&=&\dot I_{\mathrm {ca}}-\dot I_{\mathrm {bc}} \\[ 5pt ] &=&\left( \frac {\sqrt {3}}{2X}+\mathrm {j}\frac {1}{2X}\right)V-\left( \frac {\sqrt {3}}{2X}-\mathrm {j}\frac {1}{2X}\right)V \\[ 5pt ] &=&\mathrm {j}\frac {1}{X}V \\[ 5pt ] \end{eqnarray}
\] と求められる。

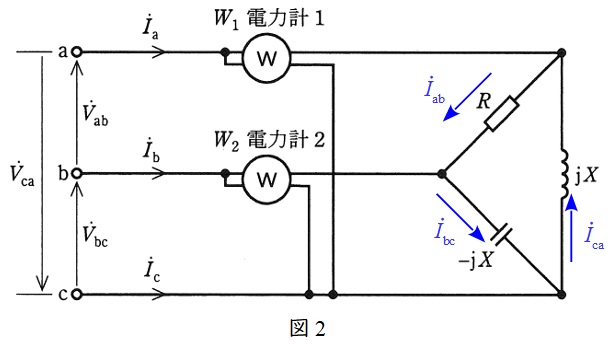
(4)解答：ニ
(1)～(3)の結果をベクトル図で表すと図3の通りとなる。
この時$ \ {\dot I}_{\mathrm {a}} \ $，$ \ {\dot I}_{\mathrm {b}} \ $，$ \ {\dot I}_{\mathrm {c}} \ $が対称三相の線電流を流すためには，各位相が$ \ 120° \ $ずつずれていなければならない。
よって，$ \ {\dot I}_{\mathrm {a}} \ $，$ \ {\dot I}_{\mathrm {b}} \ $の実部と虚部の絶対値に間に，
\[
\begin{eqnarray}
\frac {1}{R}-\frac {\sqrt {3}}{2X}&=&\sqrt {3}\cdot\frac {1}{2X} \\[ 5pt ] \end{eqnarray}
\] の関係が成り立つ。これを$ \ R \ $について整理すると，
\[
\begin{eqnarray}
\frac {1}{R}-\frac {\sqrt {3}}{2X}&=&\frac {\sqrt {3}}{2X} \\[ 5pt ] \frac {1}{R}&=&\frac {\sqrt {3}}{X} \\[ 5pt ] R&=&\frac {1}{\sqrt {3}}X \\[ 5pt ] \end{eqnarray}
\] と求められる。

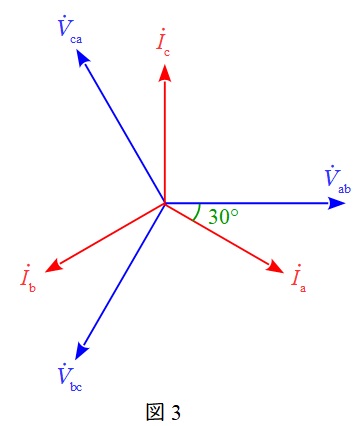
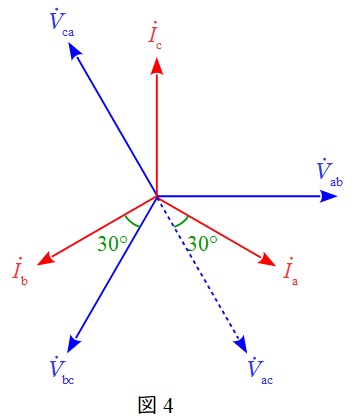
(5)解答：リ
各電力計の指示は，
\[
\begin{eqnarray}
W_{1}&=&\left| \dot V_{\mathrm {ac}}\right| \left| \dot I_{\mathrm {a}}\right| \cos \theta _{1}　（\theta _{1} \ は \ \dot V_{\mathrm {ac}} \ と \ \dot I_{\mathrm {a}} \ の位相差） \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
W_{2}&=&\left| \dot V_{\mathrm {bc}}\right| \left| \dot I_{\mathrm {b}}\right| \cos \theta _{2}　（\theta _{2} \ は \ \dot V_{\mathrm {bc}} \ と \ \dot I_{\mathrm {b}} \ の位相差） \\[ 5pt ] \end{eqnarray}
\] で求められ，各値は図4に示す通り，
\[
\begin{eqnarray}
\left| \dot V_{\mathrm {ac}}\right|&=&\left| \dot V_{\mathrm {bc}}\right|&=&V \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
\left| \dot I_{\mathrm {a}}\right| &=&\left| \dot I_{\mathrm {b}}\right|&=&\frac {1}{X}V \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
\theta _{1}=\theta _{2}&=&30^{\circ} \\[ 5pt ] \end{eqnarray}
\] となるため，$ \ W_{1} \ $と$ \ W_{2} \ $の大きさは等しく，
\[
\begin{eqnarray}
W_{1}=W_{2}&=&V\cdot \frac{1}{X}V\cos30^{\circ} \\[ 5pt ] &=&\frac{V^{2}}{X}\cdot \frac {\sqrt {3}}{2} \\[ 5pt ] &=&\frac {\sqrt {3}}{2X}V^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。