【問題】
【難易度】★★★☆☆(普通)
次の文章は,変圧器に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
変圧器の一次巻線と二次巻線とを別々の巻線にしないで,一次巻線と二次巻線の一部を共用して使用する変圧器を\( \ \fbox { (1) } \ \)といい,この変圧器の一次,二次に共通した巻線を\( \ \fbox { (2) } \ \),共通でない部分を\( \ \fbox { (3) } \ \)という。
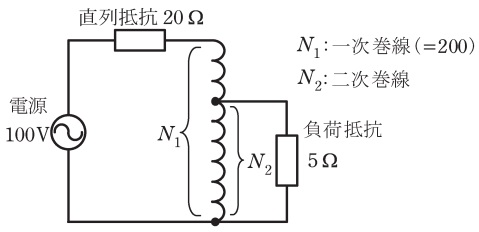
図に示すように\( \ \fbox { (1) } \ \)の一次側に\( \ 20 \ \mathrm {\Omega } \ \)の直列抵抗,二次側に\( \ 5 \ \mathrm {\Omega } \ \)の負荷抵抗を接続し,電源電圧を\( \ 100 \ \mathrm {V} \ \)とする。一次巻線の巻線を\( \ N_{1}=200 \ \)とした場合に,\( \ 5 \ \mathrm {\Omega } \ \)の負荷抵抗で消費される電力が最大となる二次巻数は\( \ N_{2}=\fbox { (4) } \ \)となり,このときの負荷抵抗の消費電力は\( \ \fbox { (5) } \ \mathrm {W} \ \)となる。なお変圧器は理想変圧器として考える。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& 線路巻線 &(ロ)& 直巻変圧器 &(ハ)& 1 \ 280 \\[ 5pt ]
&(ニ)& 三次巻線 &(ホ)& 100 &(ヘ)& 分路巻線 \\[ 5pt ]
&(ト)& 50 &(チ)& 低圧巻線 &(リ)& 高圧巻線 \\[ 5pt ]
&(ヌ)& 単巻変圧器 &(ル)& 差動変圧器 &(ヲ)& 80 \\[ 5pt ]
&(ワ)& 125 &(カ)& 直列巻線 &(ヨ)& 160 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
単相単巻変圧器に関する問題です。
単巻変圧器の各巻線や容量の名称は電験の中でも覚えにくい部類に入るものかと思います。
試験直前に必ず見直すことができるようにしておきましょう。
1.単相単巻変圧器
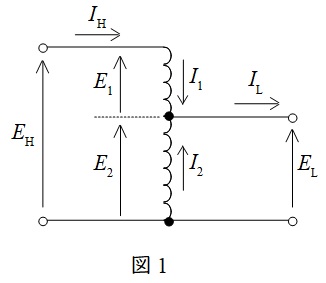
高圧側と低圧側の巻線の一部を共用する変圧器です。共用しない巻線を直列巻線(図1の\( \ E_{1} \ \)に当たる巻線),共用する巻線を分路巻線(図1の\( \ E_{2} \ \)に当たる巻線)と言います。それぞれの電圧を図1のように定義し,自己容量を\( \ P_{1} \ \),分路容量を\( \ P_{2} \ \),線路容量を\( \ P_{3} \ \)とすると,
\[
\begin{eqnarray}
P_{1} &=&E_{1}I_{1} \\[ 5pt ]
&=&\left( E_{\mathrm {H}}-E_{\mathrm {L}}\right) I_{\mathrm {H}} \\[ 5pt ]
P_{2} &=&E_{2}I_{2} \\[ 5pt ]
&=&E_{\mathrm {L}}\left( I_{\mathrm {L}}-I_{\mathrm {H}}\right) \\[ 5pt ]
P_{3} &=&E_{\mathrm {H}}I_{\mathrm {H}} \\[ 5pt ]
&=&E_{\mathrm {L}}I_{\mathrm {L}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.変圧器の巻数比と変圧比,変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \),電圧\( \ V_{1} \ \mathrm {[V]} \ \),電流\( \ I_{1} \ \mathrm {[A]} \ \),二次側の巻数\( \ N_{2} \ \),電圧\( \ V_{2} \ \mathrm {[V]} \ \),電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると,それぞれの関係は,
\[
\begin{eqnarray}
\frac {N_{1}}{N_{2}} &=&\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となります。インピーダンスは電圧を電流で割ったものであるため,一次側換算のインピーダンス\( \ Z_{1} \ \mathrm {[\Omega ]} \ \),二次側換算のインピーダンス\( \ Z_{2} \ \mathrm {[\Omega ]} \ \)とすると,
\[
\begin{eqnarray}
\frac {Z_{1}}{Z_{2}} &=&\frac {\displaystyle \frac {V_{1}}{I_{1}}}{\displaystyle \frac {V_{2}}{I_{2}}} \\[ 5pt ]
&=&\frac {V_{1}}{I_{1}}\times \frac {I_{2}}{V_{2}} \\[ 5pt ]
&=&\frac {V_{1}}{V_{2}}\times \frac {I_{2}}{I_{1}} \\[ 5pt ]
&=&\left( \frac {N_{1}}{N_{2}} \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ヌ
題意より解答候補は,(ロ)直巻変圧器,(ヌ)単巻変圧器,(ル)差動変圧器,になると思います。
ワンポイント解説「1.単相単巻変圧器」の通り,一次巻線と二次巻線を共用して使用する変圧器を単巻変圧器といいます。
(2)解答:ヘ
題意より解答候補は,(イ)線路巻線,(ニ)三次巻線,(ヘ)分路巻線,(チ)低圧巻線,(リ)高圧巻線,(カ)直列巻線,になると思います。
ワンポイント解説「1.単相単巻変圧器」の通り,単巻変圧器の一次,二次に共通した巻線を分路巻線といいます。
(3)解答:カ
題意より解答候補は,(イ)線路巻線,(ニ)三次巻線,(ヘ)分路巻線,(チ)低圧巻線,(リ)高圧巻線,(カ)直列巻線,になると思います。
ワンポイント解説「1.単相単巻変圧器」の通り,単巻変圧器の一次,二次の共通でない部分を直列巻線といいます。
(4)解答:ホ
ワンポイント解説「2.変圧器の巻数比と変圧比,変流比の関係」の通り,電源電圧\( \ E=100 \ \mathrm {[V]} \ \)及び負荷抵抗\( \ R_{1}=20 \ \mathrm {[\Omega ]} \ \)を二次換算したときの値\( \ E^{\prime } \ \mathrm {[V]} \ \)及び\( \ R_{1}^{\prime } \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
E^{\prime } &=& \frac {N_{2}}{N_{1}} E \\[ 5pt ]
&=& \frac {N_{2}}{200} \times 100 \\[ 5pt ]
&=& \frac {N_{2}}{2} \\[ 5pt ]
R_{1}^{\prime } &=&\left( \frac {N_{2}}{N_{1}}\right) ^{2} R_{1} \\[ 5pt ]
&=&\left( \frac {N_{2}}{200}\right) ^{2} \times 20 \\[ 5pt ]
&=&\frac {N_{2}^{2}}{2 \ 000} \\[ 5pt ]
\end{eqnarray}
\]
となるので,二次側の負荷抵抗\( \ R_{2}=5 \ \mathrm {[\Omega ]} \ \)に流れる電流\( \ I_{2} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{2} &=&\frac {E^{\prime }}{R_{1}^{\prime }+R_{2}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {N_{2}}{2}}{\displaystyle \frac {N_{2}^{2}}{2 \ 000}+5} \\[ 5pt ]
&=&\frac {1 \ 000N_{2}}{N_{2}^{2}+10 \ 000} \\[ 5pt ]
\end{eqnarray}
\]
となり,負荷抵抗\( \ R_{2}=5 \ \mathrm {[\Omega ]} \ \)で消費される電力\( \ P_{2} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{2} &=&R_{2}I_{2}^{2} \\[ 5pt ]
&=&5\times \left( \frac {1 \ 000N_{2}}{N_{2}^{2}+10 \ 000}\right) ^{2} \\[ 5pt ]
&=&\frac {5 \ 000 \ 000N_{2}^{2}}{N_{2}^{4}+20 \ 000N_{2}^{2}+100 \ 000 \ 000} \\[ 5pt ]
&=&\frac {5 \ 000 \ 000}{\displaystyle N_{2}^{2}+20 \ 000+\frac {100 \ 000 \ 000}{N_{2}^{2}}} ・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ A=\displaystyle N_{2}^{2}+20 \ 000+\frac {100 \ 000 \ 000}{N_{2}^{2}} \ \)とすると,\( \ A \ \)が最小となるとき,\( \ P_{2} \ \)が最大となるので,\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}N_{2}}=0 \ \)となる\( \ N_{2} \ \)を求めると,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}N_{2}} =2N_{2}-2\frac {100 \ 000 \ 000}{N_{2}^{3}}&=&0 \\[ 5pt ]
N_{2}&=&\frac {100 \ 000 \ 000}{N_{2}^{3}} \\[ 5pt ]
N_{2}^{4}&=&100 \ 000 \ 000 \\[ 5pt ]
N_{2}^{2}&=&10 \ 000 \\[ 5pt ]
N_{2}&=&100 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※最大電力となるとき二次側換算した負荷抵抗\( \ \displaystyle R_{1}^{\prime }=\frac {N_{2}^{2}}{2 \ 000} \ \mathrm {[\Omega ]} \ \)と負荷抵抗\( \ R_{2}=5 \ \mathrm {[\Omega ]} \ \)が等しいという条件を暗記しておいて,
\[
\begin{eqnarray}
\frac {N_{2}^{2}}{2 \ 000}&=&5 \\[ 5pt ]
N_{2}^{2}&=&10 \ 000 \\[ 5pt ]
N_{2}&=&100 \\[ 5pt ]
\end{eqnarray}
\]
と求めても問題ありません。
(5)解答:ワ
負荷抵抗\( \ R_{2}=5 \ \mathrm {[\Omega ]} \ \)で消費される最大電力\( \ P_{\mathrm {2m}} \ \mathrm {[W]} \ \)は,①式に\( \ N_{2}=100 \ \)を代入すると,
\[
\begin{eqnarray}
P_{\mathrm {2m}}&=&\frac {5 \ 000 \ 000}{\displaystyle N_{2}^{2}+20 \ 000+\frac {100 \ 000 \ 000}{N_{2}^{2}}} \\[ 5pt ]
&=&\frac {5 \ 000 \ 000}{\displaystyle 100^{2}+20 \ 000+\frac {100 \ 000 \ 000}{100^{2}}} \\[ 5pt ]
&=&\frac {5 \ 000 \ 000}{40 \ 000} \\[ 5pt ]
&=&125 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
[別解]
(4)より,
\[
\begin{eqnarray}
E^{\prime } &=& \frac {N_{2}}{2} \\[ 5pt ]
&=& \frac {100}{2} \\[ 5pt ]
&=& 50 \ \mathrm {[V]} \\[ 5pt ]
R_{1}^{\prime } &=&R_{2} \\[ 5pt ]
&=&5 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるため,\( \ R_{2}=5 \ \mathrm {[\Omega ]} \ \)に加わる電圧は\( \ \displaystyle \frac {E^{\prime }}{2}=25 \ \mathrm {[V]} \ \)である。したがって,負荷抵抗\( \ R_{2}=5 \ \mathrm {[\Omega ]} \ \)で消費される最大電力\( \ P_{\mathrm {2m}} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {2m}}&=&\frac {\displaystyle \left( \frac {E^{\prime }}{2}\right) ^{2}}{R_{2}} \\[ 5pt ]
&=&\frac {25^{2}}{5} \\[ 5pt ]
&=&125 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは