Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,インバータにより\( \ \mathrm {V/f} \ \)一定制御されている誘導電動機に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
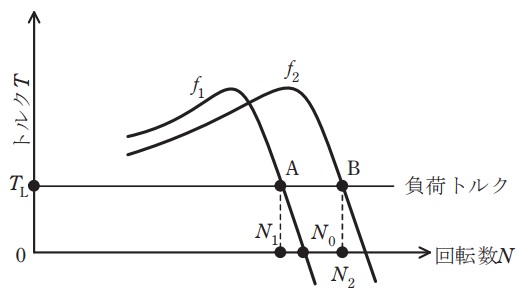
三相誘導電動機の速度制御として\( \ \mathrm {PWM} \ \)インバータを用いた\( \ \mathrm {V/f} \ \)一定制御が広く用いられている。ここで,\( \ \mathrm {V} \ \)は電動機の端子電圧,\( \ \mathrm {f} \ \)は端子電圧の周波数である。\( \ \mathrm {V/f} \ \)一定制御されている誘導電動機の定常状態のトルク特性が,端子電圧の周波数\( \ f_{1} \ \),\( \ f_{2} \ \)に対し,図のように与えられている。また,負荷のトルク特性は回転数\( \ N \ \)に関わらず\( \ T_{\mathrm {L}} \ \)一定で図のように与えられている。このとき,電動機の回転数はそれぞれ,\( \ N_{1} \ \),\( \ N_{2} \ \)である。今,この電動機が周波数\( \ f_{2} \ \)にて運転中で,回転数が\( \ N_{2} \ \)のときに,周波数\( \ f_{1} \ \)に切り換え,\( \ N_{1} \ \)まで減速して,点\( \ \mathrm {A} \ \)で負荷トルクと電動機トルクがつりあう。
\( \ N_{2} \ \)からの減速過程のうち,\( \ N_{0}<N<N_{2} \ \)では電動機は\( \ \fbox { (1) } \ \)をするので,電動機は\( \ \fbox { (2) } \ \)トルクを発生する。これにより減速する回転系としては,軸受の摩擦などを無視すると,この\( \ \fbox { (1) } \ \)のトルクと負荷トルクの合成が減速トルクとなる。
続いて,\( \ N=N_{0} \ \)まで減速すると,このとき,電動機は\( \ \fbox { (3) } \ \)で運転しているので,負荷トルクのみが減速トルクとなる。
さらに減速して,\( \ N_{1}<N<N_{0} \ \)となると,電動機は\( \ \fbox { (4) } \ \)をするので,\( \ \fbox { (5) } \ \)トルクを発生する。この区間では電動機の発生トルクは負荷トルクより小さいので,負荷トルクから電動機トルクを差し引いた差が減速トルクとして働く。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& 逆転運転 &(ロ)& 負の &(ハ)& 同期速度 \\[ 5pt ]
&(ニ)& 逆相動作 &(ホ)& 電動機動作 &(ヘ)& 逆相 \\[ 5pt ]
&(ト)& スイッチング周波数の &(チ)& 制動機動作 &(リ)& 発電機動作 \\[ 5pt ]
&(ヌ)& 拘束状態 &(ル)& インバータの &(ヲ)& 高周波の \\[ 5pt ]
&(ワ)& 加速動作 &(カ)& ゼロの &(ヨ)& 正の \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
誘導電動機の\( \ \mathrm {V/f} \ \)制御に関する問題です。
本問を解く上では「3.滑り\( \ s \ \)と同期速度\( \ N_{\mathrm {s}} \ \)及び回転速度\( \ N \ \)の関係」が最も重要な内容となります。それぞれの状態を丸暗記するのではなく,同期速度と回転速度の速い方に引っ張られるイメージをして,どのようなトルクが発生するかを理解するようにしましょう。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \),回転速度が\( \ N \ \mathrm {[{min}^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.滑り\( \ s \ \)と同期速度\( \ N_{\mathrm {s}} \ \)及び回転速度\( \ N \ \)の関係
誘導電動機は滑り\( \ s \ \)に応じて発電機もしくは電動機に状態が変化します。
①\( \ 0≦s≦1 \ \)のとき
固定子磁界の同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)の方が回転子の回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)より大きい状態であるため,誘導電動機の状態となります。したがって,回転子には正のトルクが発生することになります。
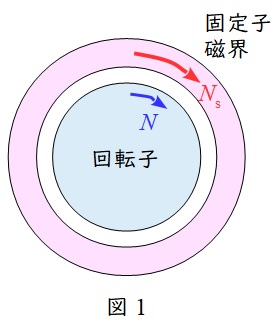
②\( \ s<0 \ \)のとき
回転子の回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)の方が固定子磁界の同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)より大きい状態であるため,誘導発電機の状態となります。このとき,回転子には負のトルクが発生し,回生制動の状態となり電源側にエネルギーが回生されます。
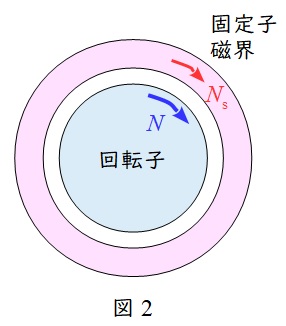
③\( \ s>1 \ \)のとき
固定子磁界の同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)と回転子の回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)が逆方向の状態となるため,逆相制動の誘導電動機の状態となります。このとき,回転子には大きな負のトルクがかかり逆相制動と呼ばれる状態となります。固定子入力の\( \ 3 \ \)相のうち\( \ 2 \ \)相を入れ替えたとき,この状態になります。
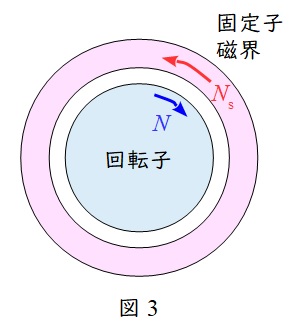
4.\( \ V / f \ \)制御の概要
\( \ V / f \ \)の値を一定に保つことで,磁気飽和が起こらないように磁束密度を一定として制御を行う方法です。
一次誘導起電力(相電圧)\( \ E_{1} \ \)と一次周波数\( \ f \ \)には,一次巻線係数\( \ K_{1} \ \),最大鎖交磁束\( \ \phi \ \),一次巻線の巻数\( \ N_{1} \ \)とすると,
\[
\begin{eqnarray}
E_{1}&=&4.44K_{1}f\phi N_{1} \\[ 5pt ]
\end{eqnarray}
\]
の関係があり,\( \ \displaystyle \frac {E_{1}}{f} \ \)を一定とすれば,\( \ \phi \ \)は一定に保つことができるようになります。したがって\( \ V / f \ \)制御では,電源の電圧と周波数の比を一定とさせます。
【解答】
(1)解答:リ
題意より解答候補は,(イ)逆転運転,(ニ)逆相動作,(ホ)電動機動作,(チ)制動機動作,(リ)発電機動作,(ワ)加速動作,になると思います。
ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)」及び「3.滑り\( \ s \ \)と同期速度\( \ N_{\mathrm {s}} \ \)及び回転速度\( \ N \ \)の関係」の通り,周波数が\( \ f_{2} \ \)から\( \ f_{1} \ \)に変化すると同期速度は\( \ N_{0} \ \)に変化するので,回転子の回転速度の方が同期速度より大きい状態となるため,発電機動作となります。
(2)解答:ロ
題意より解答候補は,(ロ)負の,(カ)ゼロの,(ヨ)正の,等になると思います。
ワンポイント解説「3.滑り\( \ s \ \)と同期速度\( \ N_{\mathrm {s}} \ \)及び回転速度\( \ N \ \)の関係」の通り,発電機の状態となるため,回転子には負のトルクが発生します。
(3)解答:ハ
題意より解答候補は,(ハ)同期速度,(ヘ)逆相,(ヌ)拘束状態,等になると思います。
\( \ N_{0} \ \)は周波数が\( \ f_{1} \ \)に変化したときの同期速度となります。
(4)解答:ホ
題意より解答候補は,(イ)逆転運転,(ニ)逆相動作,(ホ)電動機動作,(チ)制動機動作,(リ)発電機動作,(ワ)加速動作,になると思います。
ワンポイント解説「3.滑り\( \ s \ \)と同期速度\( \ N_{\mathrm {s}} \ \)及び回転速度\( \ N \ \)の関係」の通り,\( \ N_{1}<N<N_{0} \ \)の状態においては,同期速度の方が回転子の回転速度より大きい状態であるため,電動機動作となります。
(5)解答:ヨ
題意より解答候補は,(ロ)負の,(カ)ゼロの,(ヨ)正の,等になると思います。
ワンポイント解説「3.滑り\( \ s \ \)と同期速度\( \ N_{\mathrm {s}} \ \)及び回転速度\( \ N \ \)の関係」の通り,電動機の状態となるため,回転子には正のトルクが発生します。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは